射影定理五应用

◇ 山东 楚凌霞

直角三角形的射影定理给出了直角三角形中边之间的关系,利用其求解的关键是把握好其中的比例关系,根据已知的两条边来求解另外一边的长度.由此可以用来处理一些相关的问题,本文结合实例加以剖析.

1 求解边长

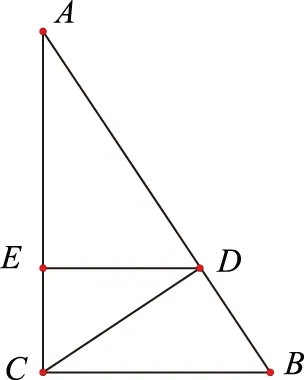
图1

分析结合题目条件可知CD，DE分别是Rt△ABC和Rt△ACD斜边上的高,故通过直角三角形的射影定理建立相应的关系式来求解对应的边长.

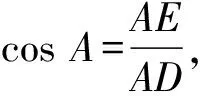
2 求解比值

分析先设出AD的长度,利用直角三角形的射影定理建立相应的方程,求出对应的边长,再利用直角三角形的射影定理得到相应的边长关系式,进而求得相应的比值.

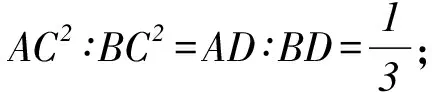
3 证明等式

图2

分析根据直角三角形的射影定理,并结合边长的关系与直角三角形相似等知识加以转化,从而证得相应的等式成立.

证明由于CD是Rt△ABC斜边AB上的高,根据直角三角形的射影定理,可得AC2=AD·AB,而AB=AF+FB,所以AC2=AD·AF+AD·FB.

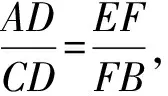
4 证明比例关系

图3

分析根据直角三角形的射影定理、相似三角形等建立相应的比例关系式,再结合所要证明的结论加以合理转化.

5 证明相似

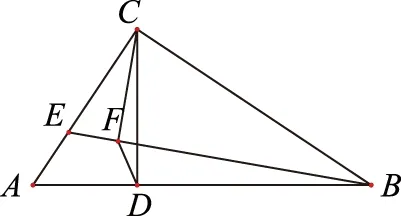
图4

分析根据直角三角形的射影定理建立相应直角三角形中边与边之间的数量关系,并合理变形来建立相似三角形问题的比例关系式，从而达到证明的目的.