高一数学测试

一、选择题(本大题共12小题,计60分)

1.已知点A(1,2)、B(5,6),则线段AB中点的坐标为( )

(A)(2,3) (B)(3,2)

(C)(3,4) (D)(4,3)

2.已知点A(-a,3),点B(5,-a),直线AB的斜率为1,则a的值为( )

(A)4 (B)-3 (C)3 (D)-4

3.在∆ABC中,sinA∶sinB∶sinC=2∶3∶4,那么cosC等于( )

5.已知∆ABC中,AB=6,∠A=30°,∠B=120°,则∆ABC的面积为( )

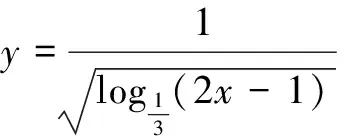
8.若AC<0,BC>0,则直线Ax+By+C=0不通过第( )象限

(A)一 (B)二 (C)三 (D)四

9.若圆C的半径为1,其圆心与点(1,0)关于直线y=x对称,则圆C的标准方程为( )

(A)x2+(y-1)2=1

(B)x2+(y+1)2=1

(C) (x-1)2+y2=1

(D) (x+1)2+y2=1

(A)1 (B) 2 (C) 3 (D) 4

二、填空题(本大题共4小题,计20分)

13.直线5x-12y-2=0与5x-12y+15=0之间的距离为______.

14.已知点A(-4,1)、B(3,-1),若直线y=kx+2与线段AB恒有公共点,则实数k的取值范围是______.

三、解答题(本大题共6小题,计70分.解答应写出必要的文字说明、证明过程或演算步骤)

17.(本小题满分10分)在∆ABC中,a、b、c分别是A、B、C的对边.

(2)若c=2acosB,试∆ABC判断的形状.

18.(本小题满分12分)根据下列条件分别求出直线的方程，并将其结果保留为一般式.

(2)过点(2,0)及(0,-3)；

(3)过点(2,3),且与x-y-3=0垂直.

19.(本小题满分12分)已知圆C经过点A(2,-1),和直线x+y=1相切,且圆心在直线y=-2x上， 圆心横坐标不大于2.

(1)求圆C的方程;

(2)已知直线l经过原点,并且被圆C截得的弦长为2,求直线l的方程.

(1)求A;

21.(本小题满分12分),如图，经过村庄A有两条夹角为60°的公路AB、AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N(异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,可以使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).

22.(本小题满分12分)已知函数

f(x)=-2x2+3x.

(1) 设函数g(x)=f(x)+mx(m∈R).

① 若g(x)在[1,+∞)单调减,求m的取值范围;

② 已知函数y=g(x),x∈[1,2]的最小值为-8,求m的值.

参考答案

一、选择题

1.C；2.D;3.D;4.A;5.C;6.D;

7.B;8.B;9.A;10.D;11.C;12.B.

二、填空题

三、解答题

17.(1)在∆ABC中，由正弦定理，得

(2)由条件及余弦定理，得

整理可得a=b,故∆ABC是等腰三角形.

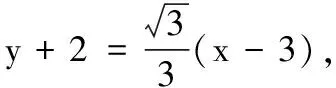
(3)设直线方程为x+y+m=0,将点(2，3)坐标代入，得m=-5.

故直线方程为x+y-5=0.

19.(1)设圆心的坐标为C(a,-2a),则

解得a=9(舍)或a=1.

故圆心C(1，-2)，

(2)①当直线l的斜率不存在时，直线l的方程为x=0,此时直线l被圆C截得的弦长为2，满足条件.

综上，直线l的方程为x=0或3x+4y=0.

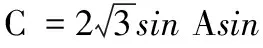
在∆ABC中，由a2=b2+c2-2bccosA=9,可得a=3.

在∆APM中，cos∠AMP=cos(60°+θ)，故θ∈(0,120°).

答：设计∠AMN为60°时，工厂产生的噪声对居民的影响最小.

22.(1)g(x)=-2x2+(m+3)x.

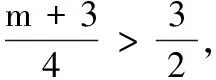
综上，m=-3.

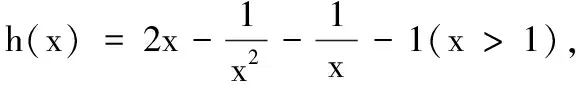
设φ(x)=2x3-x2-x-1(x>1)，则φ(1)φ(2)=-9<0，φ(x)在(1,2)内有零点.

任取1

由1

于是，有φ(x1)-φ(x2)<0,即φ(x1)<φ(x2)，φ(x)在(1,+∞)单调递增，可得φ(x)在(1,+∞)内有唯一的零点.