探究建立函数模型，提升数学建模素养

李建波

【摘要】本文选取一道生活中的建模实例，从实际问题出发，通过分析探究、交流讨论、总结归纳、深化反思等数学活动引导学生建立完整的数学模型解决实际问题，从而深化数学建模思想，使学生全面认识数学建模的全过程。因此本文是从建立函数模型出发，综合运用数学知识、思想和方法，提升数学建模素养，让学生从不同的角度理解数学的魅力。

【关键词】数学建模   函数模型   课堂实录

【中图分类号】G633.6

【文献标识码】A

【文章编号】1992-7711（2020）16-092-01

什么是数学模型呢？数学模型指为了解决实际问题，而对其进行抽象、简化后得到的数学关系结构，比如：数学概念、公式、方程、不等式、几何图形等。这些数学模型是日常生活中的人们为了解决实际问题，逐步建立起来的。而建立数学模型的过程，我们称之为数学建模。今天老师也带来了一个生活中的实际问题，我们就用数学建模的方法来解决这样的问题。

现实问题：现在许多家庭都以天然气为烧水做饭的燃料，节约使用天然气就是一个非常现实的问题。一般来说， 天然气灶是通过旋转按钮来控制燃气消耗流量的。 燃气消耗流量随着旋转位置变化而变化， 故燃气消耗量与按钮位置是函数关系。 因此问题就是：燃气灶旋转按钮在什么位置时， 烧开一壶水的燃气消耗量最少？

问题分析： 一般来说， 关闭燃灶时旋转按钮是竖直方向的， 随着按钮旋转角度逐渐增大， 燃气消耗流量也逐渐增大， 火也就越旺盛。当按钮旋转角度非常小时， 燃气消耗流量也非常小， 甚至点火后的热量不足以将一壶水烧开时;当旋转角度逐渐增大时， 燃气消耗流量也会逐渐增大， 烧水所需消耗的燃气量就会减少。但是， 当旋转角度很大（甚至最大时）， 燃气不一定都能充分燃烧提供热量，  烧开一壶水的燃气用量也会比较大。

那么，按钮旋转多大角度时，燃气消耗量最少呢？

我们不能测出所有旋转角度对应的燃气消耗量。于是我们试图通过实验给出几组数据， 然后利用这些数据拟合函数， 从而求出烧开一壶水时燃气最小消耗量。

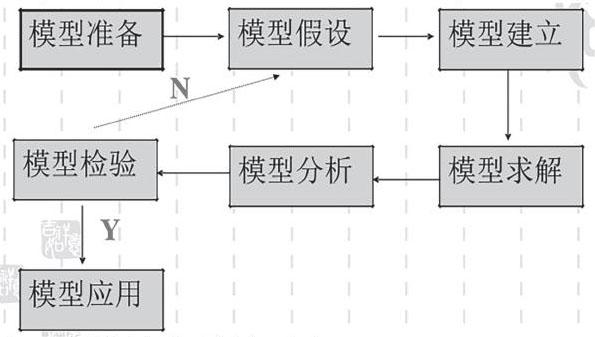
一、模型假设

（1）每次实验环境温度一样——（在同一实验室进行即可）

（2）每次试验用水量一样——（用量筒测量即可）

（3）每次烧水时水壶的起始温度一样——（烧开的第一壶水舍弃）

（4）每个按钮旋转位置都对应一个旋转角度

（5）关闭燃气灶的按钮所在的位置对应的旋转角度为0°

（6）按钮旋转的最大角度为90°

二、模型建立

（1）燃气灶按钮旋转选择5个不同位置， 旋转角度分别为18°、36°、54°、72°和90°。

备注：理论上实验选取位置数越多，实验结果越精确，但是数据测量也就越复杂。

（2）在选取的5个位置上. 分别记录烧开一壶水时所需要的燃气量。

（3）根据收集的数据，画出散点图。

三、模型求解

观察散点图， 这些点的连线是一个“U”型曲线， 根据这些点的分布情况， 我们可以可以考虑用二次函数y=ax2+bx+c模型来近似刻画烧开一壶水所消耗燃量y与按钮旋转角度x的函数关系式。

设二次函数y=ax2+bx+c取三对数据代入函数即可求出函数表达式。

不妨取（18，0.130）、（36，0.122）和（90，0.172）代入函数得：

则函数表达式为：

y=1.9033×10-5x2-1.4722×10-3x+1.5033×10-1

由二次函数性质知：

因此，当按钮旋转到39°时，烧开一壶水所需天然气最少为0.1218m3 .

四、模型检验

用与前面五组实验相同的条件， 将按钮旋转到39°的位置上， 检测所需消耗的燃气量。

若测量结果与计算结果基本吻合， 则所求的函数模型是有效的。若两者结果相差比较大， 那建立的模型就不是最优的， 我们要返回“建立函数模型”部分， 重新选择新函数。

结论：实验检测结果与函数计算值基本吻合， 误差很小， 几乎可以忽略不计， 因此我们建立的函数模型很好。

五、模型应用

通过这个实验结果， 我们知道以后烧水做饭时， 为了节约天然气资源， 尽量将燃气灶按钮旋转到39°左右的地方。

总结数学建模过程：

根据这节课的内容，我写了一句话送给大家：数学无处不在，模型到处都有，建模是数学的灵魂。

【注：本文系广东教育学会教育科研规划小课题“新疆班学生平面向量学习障碍及其解决策略研究”成果（课题编号：GDXKT23597）】

【參考文献】

[1]贺君明.高中数学建模与教学设想设 [J].读写算：教育教学研究， 2011（14）：149-151.

[2]童玉峰. 初中数学常用概念问题链教学的课例探究[J]. 吉林教育， 20l5 （25）： 59-60.