非局部问题在第二边界条件下解的存在性
叶红艳,索洪敏,李 伟,袁 恋
(贵州民族大学 数据科学与信息工程学院,贵阳 550025)
0 引言
文献[1]考虑如下方程:
其中Ω⊆RN是一个光滑有界区域,N≥3,1
(1)

(2)
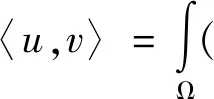
(3)
其中C,C1,C2,…表示各种正常数,在不同的行或段落它们可以表示不同的正常数.而-<λ1<λ2≤…≤λj≤…是特征值,φj是特征值所对应的特征函数.
1 主要结论
定义能量泛函为:
(4)
如果∃u∈H1(Ω),使得对∀v∈H1(Ω)都有:

(5)
则称u是问题(1)的弱解.
定理1假设1 首先证明Iμ(u)满足PS条件. 引理1设1 证明设{un}⊂X是泛函Iμ的一个PS序列,满足: (6) (7) 当n→时,有εn→0.由式(6)和式(7),可得: (8) 根据式(7),可得: (9) 其中u-=max{-u,0}.由式(6),式(8)和式(9),可推断出|Iμ(un)-〈Iμ′(un),un-〉|≤C,可得: (10) 采用反证法,假设‖un‖→.首先证明在X中un+是有界的,因此假设‖un+‖→.根据式(10)知un-是无界的.令因{vn}在X中是有界的,存在v∈X使得: (11) 根据式(10),存在δ>0满足: ‖un-‖≥δ‖un+‖2,(n→). (12) (13) 即: 其中v≠0且v≤0,这是矛盾的,因λ不是第一特征值.因此推断出在X中{un}是有界的. 证明设{un}⊂X是泛函Iμ的PS序列,满足: Iμ(un)→c,|〈Iμ′(un),h〉|≤εn‖h‖,∀h∈X. (14) 当n→时,有εn→0.由引理1知{un}是有界的.因此,存在序列{un}的一个子列(仍记为{un})以及u⊂X,使得: (15) 因{un+}在X中是有界的,根据文献[6]中的推论,可得{un+}在L2*(Ω)中也是有界的.从而存在序列{un+}的一个子列(仍记为{un+})以及u+⊂X,在L2*(Ω)中有un+→u+.由式(3)和式(4),可得: (16) (17) 及根据Brezis-Lieb′s引理,可得: (18) 由式(18),可得: (19) 另一方面,由式(14)并再次运用Brezis-Lieb′s引理,可得: (20) 考虑如下泛函Iμ+:X→R, 其中Iμ+∈C1及临界点u+满足u+≥0,同样对于Iμ也是成立的. 引理4对任意的μ>0.则平凡解μ≡0是能量泛函Iμ+的局部极小值点. 引理5在一个有界集中,对任意的μ>0.则存在t0,使得Iμ+(t0φ1)≤0. 证明用φ1表示与特征值λ1相关联的正特征函数,对t>0,有: 因λm<λ<λm+1及1 其中: τ+={γ∈C([0,1],X);γ(0)=0,γ(1)=t0φ1}. 为了得到负解,考虑如下泛函Iμ-:X→R, 其中Iμ-∈C1及临界点u-满足u-≤0,同样对于Iμ也成立.将再次应用山路引理,得到Iμ-的一个临界点. 引理6对任意的μ>0.则平凡解μ≡0是能量泛函Iμ-的局部极小值点. 引理7在一个有限集中,对任意的μ>0.则存在t0,使得Iμ-(-t0φ1)≤0. 证明对t>0,有: 因λm<λ<λm+1及1 其中: τ-={γ∈C([0,1],X);γ(0)=0,γ(1)=-t0φ1}.2 PS条件





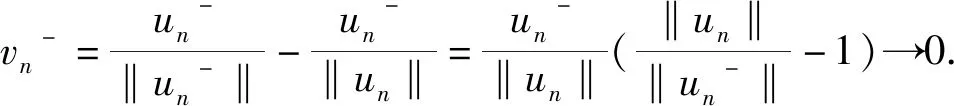




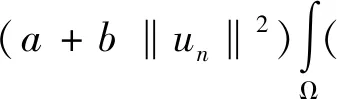

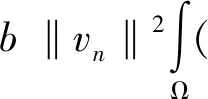


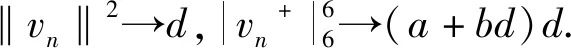
3 问题(1) 第一个解的存在性


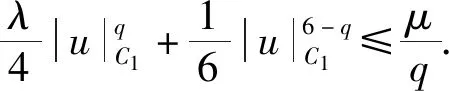


4 问题(1) 第二个解的存在性