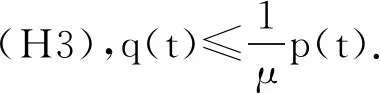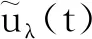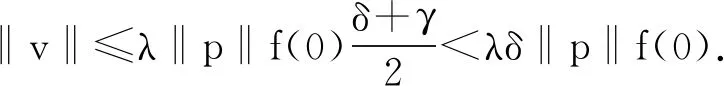一类带变号权函数的二阶差分方程Dirichlet边值问题正解的存在性
张亚莉
(西北师范大学数学与统计学院, 兰州 730070)
(2010 MSC 26A33)
1 引 言
近年来,微分和差分方程边值问题正解的存在性引起了许多学者的关注[1-11].然而,就我们所知,相应的差分方程边值问题的研究工作却相对较少.特别地, Zhang等[1]运用临界点理论研究了二阶差分方程Dirichlet边值问题
Δ2u(t-1)+λf(u(t))=0, t∈[1, T]Z,
u(0)=u(T+1)=0
(1)
Δ2u(t-1)+λa(t)f(u(t))=0, t∈[1, T]Z,
u(0)=u(T+1)=0
(2)
文献[1-2]分别在权函数a(t)=1和a(t)≥0情形下研究了非线性差分方程边值问题正解的存在性.我们自然要问:当二阶差分方程权函数变号时,正解的存在性又将如何?本文在权函数变号的情况下研究问题(2)的正解的存在性,所用方法为Leray-Schauder不动点定理.
记G(t,s)为问题Δ2u(t-1)=0, t∈[1, T]Z, u(0)=u(T+1)=0的Green函数,a+(t)=max{0,a(t)}, a-(t)=max{0,a(t)},t∈[1,T]Z.本文总假定:
(H1) λ是一个正参数;
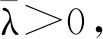
(H3) a:[1,T]Z→R,a不恒为0,且存在常数μ>1使得
t∈[0,T+1]Z.
本文主要结果如下:
定理1.1假设条件(H1)~(H3)成立.则存在λ*>0,使得当0<λ<λ*时问题(2)至少存在一个正解.
2 预备知识

引理2.1(Leray-Schauder 不动点定理[12]) 设E是Banach空间,算子A:E→E全连续.若集合{x|x∈E,x=θAx,0<θ<1}是有界的,则A在闭球T中必有不动点,其中T={x|x∈E,‖x‖≤R},R=sup{‖x‖|x=θAx,0<θ<1}.
引理2.2设h:[1,T]Z→R.则二阶线性差分方程Dirichlet边值问题
Δ2u(t-1)=-h(t), t∈[1, T]Z,
u(0)=u(T+1)=0
(3)
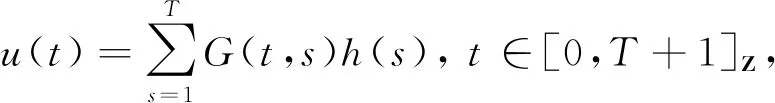
证明 只需验证u(t)满足问题(3).事实上,
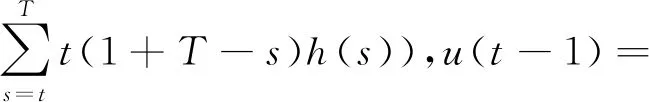
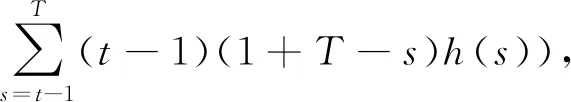
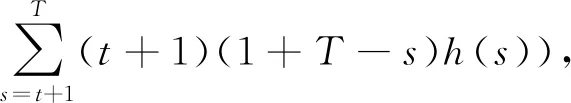
所以
Δ2u(t-1)=u(t+1)-2u(t)+u(t-1)=
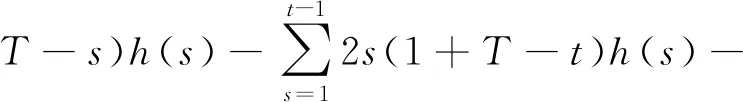
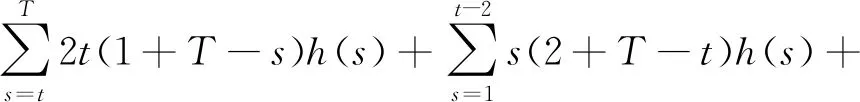
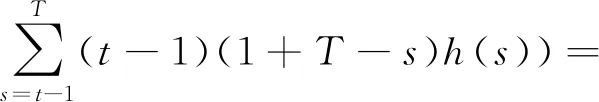
s(T-t))h(s)+(t-1)(1+T-s)h(t-1)+
t(T-t)h(t)-2(t-1)(1+T-t)h(t-1)+
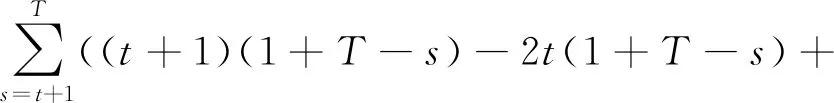
(t-1)(1+T-s))h(s)-2t(1+
T-t)h(t)+(t-1)(2+T-t)h(t-1)+
(t-1)(1+T-t)h(t))=
-h(t).
另一方面,易证u(0)=u(T+1)=0.因而u(t)满足问题(3).
Δ2u(t-1)+λa+(t)f(u(t))=0, t∈[1, T]Z
u(0)=u(T+1)=0
(4)
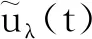
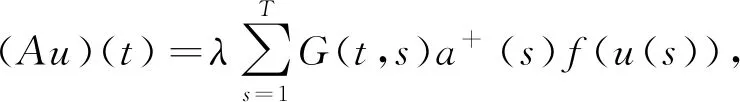
t∈[0,T+1]Z
(5)
显然,A(X)⊂X,A是全连续算子,且A的不动点就是问题(4)的解.由于f连续,f(0)>0,取充分小的ε>0使得
f(u)≥δf(0), 0 (6) (7) 所以 (8) 证毕. 定理1.1的证明 令 即 (9) q(t)|f(u)|≤γp(t)f(0), 0 (10) 固定δ∈(γ,1)并设λ*>0,使得当0<λ<λ*时有 (11) (12) 对于0<λ<λ*,设vλ(t)是问题 (13) 对任意的w∈X,由引理2.2定义算子 w(s))),t∈[1,T]Z (14) 显然T(X)⊂X,T是全连续算子,且T的不动点就是问题(13)的解.由引理2.1,设v∈X,0<θ<1,满足v=θTv.则 (15) 我们断言 ‖v‖≠λδf(0)‖p‖ (16) 反设‖v‖=λδf(0)‖p‖.则 (17) 且 ‖p‖≤λ*δf(0)‖p‖ (18) 由(12)式知 (19) 结合(15)和(19)式得 根据引理2.1,T存在一个不动点vλ(t)满足‖vλ‖≤λδf(0)‖p‖,且 从而uλ(t)是问题(2)的一个正解.证毕.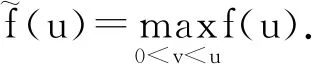
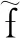
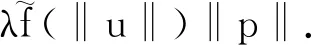
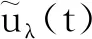
3 主要结果的证明