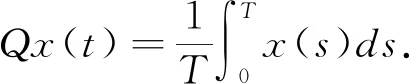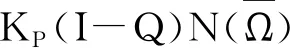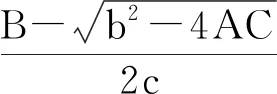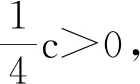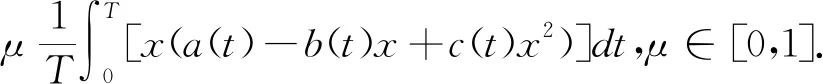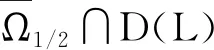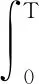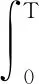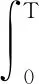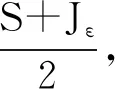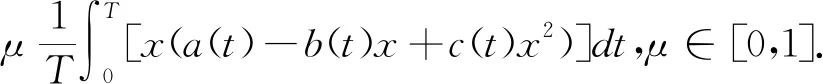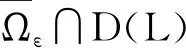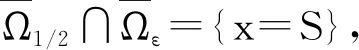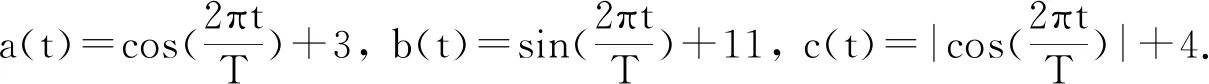一类非自治三阶常微分方程周期解的存在性
杨虎军, 韩晓玲, 罗 强
(西北师范大学数学与统计学院, 兰州 730070)
(2010 MSC 34B15)
1 引 言
具有周期解的常微分方程在物理学,天文学,生物数学等领域中有广泛应用[1-2].最近几十年,许多学者致力于研究常微分方程周期解的存在性并取得了丰富的结果[3-10].如Araujo[7]讨论了非自治二阶常微分方程
x″+a(t)x-b(t)x2+c(t)x3=0
(1)
正周期解的存在性,其中a(t),b(t),c(t)是连续的T-周期函数,满足0 受上述工作的启发,本文将此方程推广到三阶情形,并运用Mawhin延拓定理研究了非自治三阶常微分方程 x‴-a(t)x+b(t)x2-c(t)x3=0 (2) 正周期解的存在性,其中a(t),b(t),c(t)是连续的T-周期函数,满足0 设C1([0,T])为定义在[0,T]上的1次连续可微实值函数在范数‖x‖C1=max{|x|,下的Banach空间,其中|x| 定义2.1[11]设X和Y为实Banach空间,L:D(L)⊂X→Y是一个线性映射.如果L满足 (i) Im(L)是Y的闭子空间; (ii) dimKerL=codimIm(L)<+, 则称L是一个零指标的Fredholm映射. 下面给出本文的主要工具定理Mawhin延拓定理. (i) Lx≠λNx, ∀x∈∂Ω∩D(L),λ∈(0,1); (ii) QNx≠0, ∀x∈KerL∩∂Ω; (iii) deg{JQN, Ω∩KerL, 0}≠0, 定理3.1设a(t),b(t),c(t)是连续的T-周期函数, 满足 0 0 (3) 这里a,A,b,B,c,C是正常数,满足 (4) 周期T满足 (5) 证明 考虑Banach空间X=Y={x∣x∈C(R,R),x(t+T)=x(t),∀t∈R},其范数为‖x‖Y=|x|,这里|x|定义线性算子L:D(L)⊂X→Y Lx=x‴, x∈D(L) (6) 其中 D(L)={x|x(i)(0)=x(i)(T), i=0,1,2, x‴∈C(R,R)}. 定义非线性算子N:Y→Y如下: Nx=a(t)x-b(t)x2+c(t)x3 (7) 不难验证KerL=R,且 因此算子L是一个零指标的Fredholm映射. 其中 则算子QN:X→Y和KP(I-Q)N:X→X为 记 (8) 是Y中的开集,这里 (9) (10) 由(4)式可知,J和S的定义是合适的.由(3),(4)式可知,对任意t∈[0,T],有 (11) (12) 由(3),(11),(12)式可知 即 (13) 由(3),(11),(12)式可知 a(t)-b(t)S+c(t)S2= 即 a(t)-b(t)S+c(t)S2<0 (14) 设0<λ<1 且存在x使得 x‴-λa(t)x+λb(t)x2-λc(t)x3=0 (15) 将(15)式两边同时乘以x′并且在[0,T]上积分得 λc(t)x3x′]dt=0 (16) 由分部积分法得 (17) 将(17)式代入(16)式得 λc(t)x3x′]dt=0. 由(8)式可知,若x∈∂Ω1/2,则有S≤|x|≤J1/2.由(3),(11),(12)式可知,于是 这里γ是H2(0,T)嵌入到C1([0,T])中的嵌入常数.矛盾.从而对Ω=Ω1/2,定理2.3的条件(i)成立. 取x∈∂Ω1/2∩KerL.则x=S或x=J1/2.由(13),(14)式可知,∀x∈∂Ω1/2∩KerL,有 (18) 因此,对Ω=Ω1/2,定理2.3的条件(ii)成立. 由(18)式可知 H(x,μ)≠0, ∀x∈KerL∩∂Ω1/2. 由拓扑度的同伦不变性有 deg(QN,KerL∩Ω1/2,0)= KerL∩Ω1/2,0)= 下证方程(2)存在第二个解.记 (19) 是Y中的开集.由(12)式可知,存在足够小的ε,使得对t∈[0,T]有 (20) 于是 (21) 由(14)式可知 a(t)-b(t)S+c(t)S2<0 (22) 设0<λ<1且存在x使得 x‴-λa(t)x+λb(t)x2-λc(t)x3=0 (23) 将(23)式两边同时乘以x′并且在[0,T]上积分得 λc(t)x3x′]dt=0 (24) 将(17)式代入(24)式得 λc(t)x3x′]dt=0. 由(19)式知,若x∈∂Ωε,则有Jε≤|x|≤S.由(3),(20)式可知,A+BS+CS2>0.于是 这里γ是H2(0,T)嵌入到C1([0,T])中的嵌入常数.矛盾.因而对Ω=Ωε,定理2.3的条件(i)成立. 取x∈∂Ωε∩KerL.则有x=S或x=Jε.由(21),(22)式可知,∀x∈KerL∩∂Ωε,有 (25) 因此对Ω=Ωε,定理2.3的条件(ii)成立. 由(25)式可知 H(x,μ)≠0, ∀x∈KerL∩∂Ωε. 由拓扑度的同伦不变性, 有 deg(QN,Ωε∩KerL,0)= Ωε∩KerL,0)=-1≠0, b2-4AC=100-80=20>0, 若周期T满足 则定理3.1保证了方程 至少有两个正的T-周期解.2 预备知识
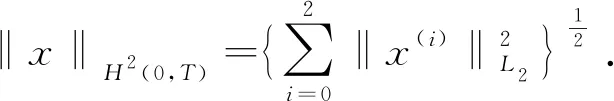


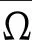
3 主要结果