Continuous generalized metric spaces
YU Jun-Che
(College of Mathematics, Sichuan University, Chengdu 610064, China)
Abstract: Continuous generalized metric spaces are introduced and investigated in this paper. It is shown that for such spaces, c-Scott topology is equal to the generalized Scott topology, and that a non-expansive map between such spaces is Yoneda continuous if and only if it is continuous with respect to the generalized Scott topology.
Keywords: Generalized metric space; Generalized Scott topology; c-Scott topology; Yoneda continuous(2010 MSC 06B35, 18B35, 54E35)
1 Introduction
As observed in Lawvere[1], a generalized metric space is precisely a category enriched in the quantale ([0,∞]op,+,0). So, they can be viewed as a metric counterpart of ordered sets. The investigation of such spaces is the core part the quantitative domain theory[2-7]. In particular, as metric counterpart of dcpo’s and domains, Yoneda complete generalized metric spaces and continuous Yoneda complete generalized metric spaces have been introduced and investigated in Refs.[3-4,6].
In this paper, the notion of continuous generalized metric spaces is introduced. Such spaces are a metric counterpart of continuous posets[4]in domain theory. The difference between such a space and a metric domain, i.e., a continuous Yoneda complete metric space, is that it need not be Yoneda complete. Basic properties of such spaces are investigated in this paper. Particularly, it is shown that, for such spaces, the generalized Scott topology is equal to the c-Scott topology, and that a non-expansive map between such spaces is Yoneda continuous if and only if it is continuous with respect to the generalized Scott topology.
2 Continuous generalized metric spaces
By a generalized metric on a set X, we mean a map d:X×X→[0,∞] such that d(x,x)=0 and d(x,y)+d(y,z)≥d(x,z) for all x,y,z∈X. The map d is called a generalized metric, and the value d(x,y) the distance from x to y.
A generalized metric space (X,d) is symmetric if d(x,y)=d(y,x) for all x,y∈X; separated if x=y whenever d(x,y)=d(y,x)=0; finitary if d(x,y)<∞ for all x,y∈X. A metric in the usual sense is exactly a symmetric, separated and finitary one. Given a generalized metric d on a set X, the opposite dopof d refers to the generalized metric given by dop(x,y)=d(y.x).
Example2.1(The Lawvere metric[1]) For all a,b in [0,∞], the Lawvere distance, dL(a,b), from a to b is defined to be the truncated minus b⊖a, i.e.,
dL(a,b)=b⊖a=max{b-a,0},
where, we take by convention that ∞-∞=0 and ∞-a=∞ for all a<∞. It is clear that ([0,∞],dL) is a separated, non-symmetric, and non-finitary metric space.
The opposite of the Lawvere metric is denoted by dR, i.e., dR(x,y)=x⊖y.
A non-expensive map f:(X,d)→(Y,ρ) between generalized metric spaces is a map f:X→Y such that
d(x,y)≥ρ(f(x),f(y)).
For each ordered set (X,≤), let ω(≤):X×X→[0,∞] be given by

Then (X,ω(≤)) is a generalized metric space. The correspondence (X,≤)(X,ω(≤)) defines a full and faithful functor
ω : Ord → GMet.
The functor ω has a right adjoint
τ: GMet → Ord
that maps each generalized metric space (X,d) to its underlying order (X,≤d), where
x≤dy⟺d(x,y)=0.
Let (X,d) be a generalized metric space. A weight of (X,d) is a function φ:X→[0,∞] such that
φ(x)≤φ(y)+d(x,y)
for all x,y∈X. A coweight of (X,d) is a function ψ:X→[0,∞] such that
ψ(y)≤ψ(x)+d(x,y)
for all x,y∈X. Said differently, a weight of (X,d) is a non-expansive map φ:(X,d)→([0,∞],dR) and a coweight of (X,d) is a non-expansive map ψ:(X,d)→([0,∞],dL). It is easily verified that for each x∈X, d(-,x) is a weight of X and d(x,-) is a coweight of X.
Let PX be the set of all weights of a generalized metric space (X,d). For any φ,ψ∈PX, let
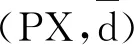
Lemma2.2(Yoneda lemma[1]) Let (X,d) be a generalized metric space. Then

for all x∈X and φ∈PX.
Let (X,d) be a generalized metric space and φ a weight of (X,d). An element a∈X is called a colimit of φ if

for all y∈X.
Let (X,d) be a generalized metric space. For each weight φ and each coweight ψ of (X,d), the tensor product of φ and ψ [Ref. 8] is an element in [0,∞], given by

Definition2.3[8]Let (X,d) be a generalized metric space, a weight φ of (X,d) is flat if infx∈Xφ(x)=0 and φ⊗max{ψ1,ψ2}=max{φ⊗ψ1,φ⊗ψ2} for any coweights ψ1,ψ2of (X,d).
For each x in a generalized metric space (X,d), d(-,x):X→[0,∞] is easily verified to be a flat weight. Flat weights can be characterized by forward Cauchy nets. A net {xi}iin a generalized metric space (X,d) is forward Cauchy[3]if
An element x∈X is a Yoneda limit[3]of {xi}iif for all y∈X,
A generalized metric space is Yoneda complete if each forward Cauchy net has a Yoneda limit.
Yoneda limits are not necessarily unique. However, if both x and y are Yoneda limits of a net {xi}i, then
d(x,y)=d(y,x)=0.
So, Yoneda limits of a forward Cauchy net in separated metric spaces are unique.
A non-expansive map f:(X,d)→(Y,ρ) is Yoneda continuous if it preserves Yoneda limits in the sense that if a is a Yoneda limit of a forward Cauchy net {xi}ithen f(a) is a Yoneda limit of {f(xi)}i.
Proposition2.4[8]Let (X,d) be a generalized metric space and φ a weight of (X,d). Then φ is a flat weight if and only if there is a forward Cauchy net {xi}iin (X,d) such that φ=infisupj≥id(-,xj).
Proposition2.5[9]For each forward Cauchy net {xi}iin a generalized metric space (X,d), an element x is a Yoneda limit of {xi}iif and only if x is a colimit of the weight φ=infisupj≥id(-,xj).
As an immediate corollary we obtain that (X,d) is Yoneda complete if and only if the map

has a left adjoint, where FX denotes the set of flat weights of (X,d).
Given a partially ordered set (X,≤), consider the generalized metric space (X,ω(≤)). Then a weight ψ of (X,ω(≤)) is flat if and only if there exists a directed lower set D of (X,≤) such that ψ(x)=0 when x∈D and ψ(x)=∞ when x∉D. Furthermore, ψ has a colimit if and only if D has a join. Therefore, (X,ω(≤)) is Yoneda complete if and only if (X,≤) is directed complete. Conversely, the underlying order of each Yoneda complete generalized metric space is directed complete, see Ref. [10, Proposition 4.5].
Definition2.6Let (X,d) be a generalized metric space and let F*X denotes the subset of FX consisting of flat weights that have a colimit. We say (X,d) is continuous if the map

Definition2.7A separated generalized metric space (X,d) is said to be a metric domain if it is both continuous and Yoneda complete.
Said differently, a separated generalized metric space (X,d) is a metric domain if the map

has a left adjoint which is itself a right adjoint.
Definition2.8[3-4]An element a in a generalized metric space is compact if for every forward Cauchy net {xi}iwith a Yoneda limit x, d(a,x)=infisupj≥id(a,xj). A separated generalized metric space is algebraic if every element in (X,d) is a Yoneda limit of a forward Cauchy net consisting of compact elements.
Proposition2.9[11]An element a is compact in a generalized metric space (X,d) if and only if for each flat weight φ with a colimit it holds that d(a,colim φ)=φ(a).
It is proved in Ref. [12] that a Yoneda complete and algebraic generalized partial metric space is continuous. Similarly, we have the following proposition for generalized metric spaces.
Proposition2.10Algebraic generalized metric spaces are continuous.
ProofFor each x∈X, take a forward Cauchy net {ai}iof compact elements in X with x as a Yoneda limit and let φx=infisupj≥id(-,aj). Then for every flat weight φ of (X,d) with a colimit,
d(x,colim φ).
Example2.11The generalized metric space (Q∩[0,∞],dL) is algebraic, hence continuous. But it is not Yoneda complete.
In the following, we characterize continuous generalized metric spaces by a metric version of the "way below relation" in domain theory.
Definition2.12(way-below distance)
Given a separated generalized metric space (X,d), the way-below distance on X is the map w:X×X→[0,∞] given by
Lemma2.13Let (X,d) be a separated generalized metric space. Then for all x,y,z∈X:
(i) d(x,y)≤w(x,y);
(ii) w(x,y)≤w(x,z)+d(z,y)≤w(x,z)+w(z,y).
Consider the generalized metric space (X,ω(≤)) induced by a partially ordered set (X,≤), for any x,y∈X, it is easy to check that,
Proposition2.14A separated generalized metric space (X,d) is continuous if and only if for every x∈X, w(-,x) is a flat weight and x is a colimit of w(-,x).
ProofLet ψ be a flat weight with a colimit a. For every y∈X, w(y,x)≥ψ(y)⊖d(x,a). It follows that,


Since x is a colimit of w(-,x),



Hence (X,d) is continuous.

it follows that
φx(y)≥ψ(y)⊖d(x,colim ψ)
for every y∈X. Hence,
φx(y)≥w(y,x).
On the other hand,
φx(y)⊖d(x,x)=φx(y).
Proposition2.15(interpolation property) Let (X,d) be a continuous generalized metric space. Then for all x,y∈X,
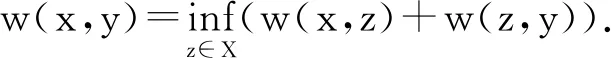

Firstly, for any ε<0, there exist a,b∈X such that w(a,y)<ε, w(b,a)<ε, it follows that φ(b)<2ε. We obtain
infx∈Xφ(x)=0.
For any coweights ψ1,ψ2on (X,d),
max{φ⊗ψ1,φ⊗ψ2}
(1)
For any a∈X,



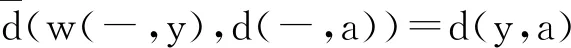
(2)
Then by the definition of way-below distance,
w(x,y)≥φ(x)⊖d(y,y)=φ(x).
It follows that
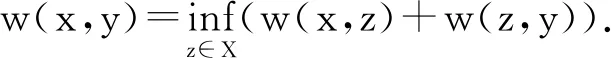
Let (X,≤) be a partially ordered set. It is not hard to see that (X,≤) is a continuous poset if and only if (X,ω(≤)) is a continuous generalized metric space. So, the functor ω preserves and reflects continuity. But, the following example shows that the functor ι does not preserves continuity.
Example2.16Let X=[0,1]∪{a}. Define a generalized metric on X as follows:

Since every element in (X,d) is compact, (X,d) is algebraic, hence continuous by Proposition 2.10. It is easily verified that (X,d) is Yoneda complete, hence (X,d) is a metric domain. But (X,≤d) is not continuous.
3 Topologies on continuous generalized metric spaces
For every generalized metric space (X,d), there is a natural topology for (X,d), namely, the open ball topology on (X,d). The open ball topology[4]]on (X,d) is the topology generated as a basis by the open balls in (X,d), where, for each x∈X and r>0, a point lies in the open ball B(x,r) with center x and radius r if the distance d(x,y) from x to y is less than r, i.e.,
B(x,r)={y∈X|d(x,y) One easily sees that, for an ordered set (X,≤), the open ball topology on (X,ω(≤)) is equal to the Alexandroff topology on (X,≤). Hence, the open ball topology is an extension of the Alexandroff topology to generalized metric spaces. As for Scott topology, in the literature there exist three ways to extend it to the metric setting. Definition3.1[3]A subset U of a generalized metric space (X,d) is generalized Scott open if for every forward Cauchy net {xi}iand every Yoneda limit x of {xi}i, if x∈U then there is some ε>0 and some index i such that the open ball B(xj,ε) is contained in U for all j≥i. The generalized Scott open subsets of (X,d) form a topology, called the generalized Scott topology on (X,d). Proposition3.2Let (X,≤) be a poset, then the Scott topology on (X,≤) and the generalized Scott topology on (X,ω(≤)) coincide. The generalized Scott topology on a generalized metric space (X,d) and Scott topology on the underlying order of (X,d) are incomparable in general. Take [0,1] with the usual metric. Then the generalized Scott topology is strictly coarser than Scott topology on its underlying order. The following example shows that not every generalized Scott open subset of a generalized metric space is open with respect to the Scott topology on its underlying ordered set. Example3.3Let X=[0,1]∪{a}. Define a map d:X×X→[0,∞] as follows: Then (X,d) is a generalized metric space and {1} is generalized Scott open. But {1} is not Scott open. RemarkIn the definition of the generalized Scott topology, we require that there exists a fixed ε such that the open ball B(xj,ε) is contained in U whenever j≥i. It is natural to ask whether this requirement can be relaxed to “for any j≥i, there exists an εjsuch that the open ball B(xj,εj) is contained in U″. The answer is negative, as we now see. We call a subset U quasi-generalized Scott open if for every forward Cauchy net {xi}iand every Yoneda limit x of {xi}i, if x∈U then there is some index i such that for all j≥i, there exists εj>0, B(xj,εj) contained in U. It is readily verified that quasi-generalized Scott open subsets form a topology on X, called the quasi-generalized Scott topology. The following example shows that the generalized Scott topology and the the quasi-generalized Scott topology are different in general. Let X={a}∪{an|n∈Z+}∪{bn∣n∈Z+}. Define d:X×X→[0,∞] as follows. Then the open ball B(a,2) is not generalized Scott open, but it is quasi generalized Scott open. Proposition3.4A subset U of a generalized metric space (X,d) is generalized Scott open if and only if for every flat weight φ, and every colimit a of φ, a∈U implies that there exist b>0 and z∈X such that φ(z) ProofNecessity. Suppose a is a colimit of a flat weight φ and a∈U. Then there exists a forward Cauchy net {xi}i∈Isuch that φ=infisupj≥id(-,xj) and a is a Yoneda limit of {xi}i∈I. Since U is generalized Scott open, there exist i∈I and b>0 such that for all j≥i, B(xj,b)⊆U. Since {xi}i∈Iis forward Cauchy, there exists i′∈I, φ(xj) φ(z) and B(z,b)⊆U. Sufficiency. Suppose a is a Yoneda limit of a forward Cauchy net {xi}i∈Iand a∈U. Let φ=infisupj≥id(-,xj), there exist b>0 and z∈X such that φ(z)0, such that φ(z) B(xj,ε)⊆B(z,b)⊆U. Proposition3.5[6]Let (X,d) be a continuous generalized metric space. B′(x,ε) is generalized Scott open for all x∈X,ε>0. Furthermore, the set {B′(x,ε)∣x∈X,ε>0}. forms a basis for the generalized Scott topology. The c-Scott topology is another way to generalize Scott topology to the metric setting. Definition3.6[11]A weight φ of a generalized metric space (X,d) is a Scott weight if φ:(X,d)→([0,∞],dR) is Yoneda contunuous. The set of all Scott weights of a generalized metric space (X,d) is denoted by SX. Definition3.7[11]The topology whose closed sets are given by {φ-1(0)∣φ∈SX} on a generalized metric space (X,d) is called the c-Scott topology on (X,d). Lemma3.8For every continuous generalized metric space (X,d), r⊖w(x,-) is a Scott weight for all x∈X,r∈[0,∞]. ProofIt is easy to verify that φ=r⊖w(x,-) is a weight of (X,d), we only need to check that, for any forward Cauchy net {ai}iwhich has a Yoneda limit a, For any b∈X, w(x,b)+w(b,a)≥w(x,b)+ Since (X,d) is continuous, Hence, Proposition3.9For a continuous generalized metric space (X,d), the c-Scott topology is equal to the generalized Scott topology. ProofSince for each x∈X and ε>0, (ε⊖w(x,-))-1(0,∞]= {y∣w(x,y)<ε}=B′(x,ε), then by Lemma 3.9, B′(x,ε) is open in the c-Scott topology. By Proposition 3.6, the c-Scott topology is finer than the generalized Scott topology. Hence, they are equal. It is known (Ref.[3, Proposition 6.9])that a non-expansive map between Yoneda complete generalized metric spaces is Yoneda continuous if and only if it is continuous with respect to the generalized Scott topology, this is also true for continuous generalized metric spaces. Proposition3.10Let (X,d) be a generalized metric space and (Y,ρ) be a continuous generalized metric space, a non-expansive map f:X→Y is Yoneda continuous if and only if f is continuous with respect to the generalized Scott topology. ProofThe necessity is contained in Ref.[3, Proposition 6.9], it remains to show that, if f is non-expansive and continuous with respect to generalized Scott topology, then for every forward Cauchy net {xi}iwith a Yoneda limit x and y∈Y, On one hand, since f is non-expansive, On the other hand, for every forward Cauchy net {ak}kwith a Yoneda limit a, It follows that If then there exists ε>0, Because Y is continuous, A=B′(y,w(y,f(x))+ε) is generalized Scott open in Y. Since f is continuous, then f←(A) is generalized Scott open in X. It is a contradiction. Hence Since (Y,ρ) is continuous, f(x) is a colimit of the flat weight w(-,f(x)), This completes the proof. In Ref.[4], Goubault-Larrecq introduced another topology, the d-Scott topology, for generalized metric spaces and showed that a non-expansive map between Yoneda complete generalized metric spaces is Yoneda continuous if and only if it is continuous with respect to the d-Scott topology, see Ref. [4, Proposition 7.4.52]. But, this is not true for continuous metric spaces, as we see now. For a generalized metric space (X,d), let (BX,≤) be the underlying order of the generalized metric space (BX,Bd) of formal balls in (X,d). Explicitly, BX={(x,r)∣x∈X,r∈[0,∞)} (x,r)≤(y,s)⟺r≥s+d(x,y). The d-Scott topology[4]on a generalized metric space (X,d) is defined to be the topology on X inherited from the Scott topology on the ordered set (BX,≤) via the embedding η:X→BX that sends each x to (x,0). Example3.11Let X=[0,1], define two maps d1,d2:X×X→[0,∞] on X as follows: (X,d1),(X,d2) are both continuous metric spaces, the identity map 1Xis non-expansive and continuous with respect to the d-Scott topology, but it is not Yoneda continuous.

