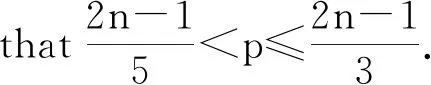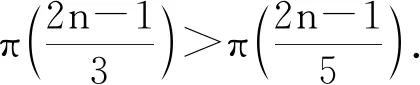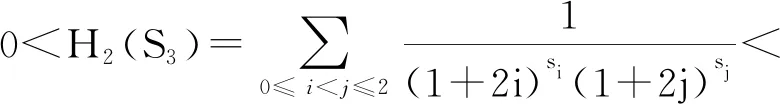On the integrality of the second elementary symmetric function of 1,1/3s1,...,1/(2n-1)sn-1

FENG Yu-Lu, ZHAO Wei

(1.College of Mathematics, Sichuan University, Chengdu 610064, China；2.Science and Technology on Communication Security Laboratory, Chengdu 610041, China)

Abstract: Let d,m and n be positive integers. In 1915, Theisinger proved that if n≥2, then the n-th harmonic sum 1+1/2+...+1/n is not an integer. In 1946, Erdös and Niven extended Theisinger′s theorem by showing that there are only finitely many positive integers n for which one or more of the elementary symmetric functions of 1/m, 1/(m+d),..., 1/(m+nd) are integers. In 2015, Wang and Hong proved that none of the elementary symmetric functions of 1, 1/3, ... ,1/(2n-1) is an integer if n≥2. In this paper, we show that if n≥2, then for arbitrary sequence Sn=(s0,s1,...,sn-1) of positive integers (note that all the si are not necessarily distinct and not necessarily monotonic), the following reciprocal power sum

Keywords: Elementary symmetric function; Integrality; p-adic valuation

1 Introduction

LetZ,Z+andQbe the set of integers, the set of positive integers and the set of rational numbers, respectively. Let d,m and n∈Z+. In 1915, Theisinger[1]proved that the n-th harmonic sum 1+1/2+...1/n is not integer if n>1. In 1946, Erdös and Niven[2]proved that there are only finitely many positive integers n for which one or more of the elementary symmetric functions of 1/m, 1/(m+d),..., 1/(m+nd)are integers. In recent years, the problem respect to the integrality was extensively extended to the general polynomial sequence[3-7].

Throughout, let k∈Z+with 1≤k≤n. By(Z+)we denote the set of all infinitepositive integers (note that all the siare not necessarily distinct and not necessarily monotonic). For any givenlet Sn{s0, s1,..., sn-1}. Associated to the infinite sequence S of positive integers, one can form a sum Hk(Sn)being the k-th elementary symmetric function of 1,1/3s1,...,1/(2n-1)sn-1defined as follows:

In 2015, Hong and Wang[6]showed that if si=1 for all integers i≥1, then Hk(sn) is never an integer for arbitrary n≥2 and k with 1≤k≤n. By the main result of Ref.[8], we know that if n≥2,then H1(sn) is never an integer. It is clear that Hn(sn)is never an integer. But the integrality problem of Hk(sn) for 2≤k≤n-1 is still open. It was conjectured that none of Hk(sn)is an integer if n≥2[8].

In this paper, we mainly concern on the integrality of the second elementary symmetric function of 1, 1/3s1,..., 1/(2n-1)sn-1. We have the following interesting result.

Theorem1.1For any infinite sequence S of positive integers and arbitrary positive integers n≥2, the sum H2(sn) is never an integer.

Evidently, Theorem 1.1 supports Conjecture 4.1 in Ref.[8].The proof of Theorem 1.1 is analytic and p-adic in character.

2 Lemmas

Clearly, one has H2(Sn)>0.

Lemma2.1[9]Let π(x)denote the number of primes no more than x. Then

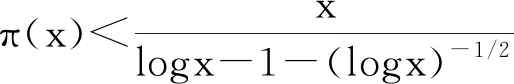
for all x≥6, and

for all x≥59.

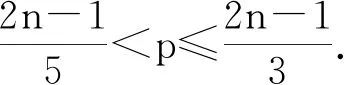
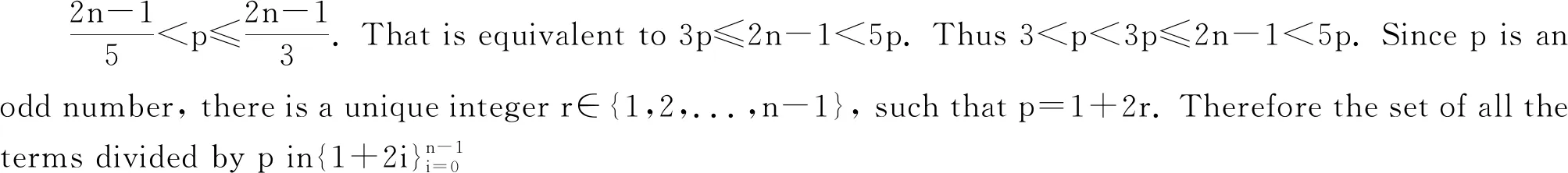
Obviously, one can split the sum H2(Sn) as H2(Sn)=H1+H2, where

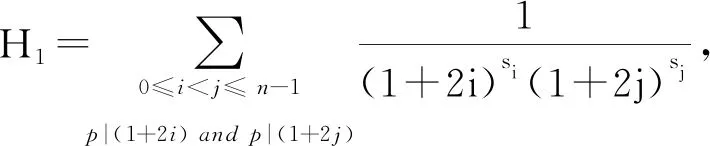
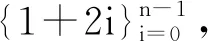
Consequently, we consider vp(H2). First, we notice the renowned fact that for any x1,x2,...,xt∈Q, one has

vp(x1+x2+...+xt)≥

min{vp(x1),vp(x2),...,vp(xt)}.

The equality holds if there exists an i such that vp(xi)

Finally, by the isosceles triangle principle[6], we can derive immediately that vp(H2(Sn))=vp(H1+H2)=vp(H1)<0. This infers that H2(Sn)is not an integer. Lemma 2.2 is proved.

3 Proof of Theorem 1.1

At first, it is obvious that H2(Sn)>0. Additionally,

Hence H2(Sn)is not an integer. Theorem 1.1 is true when n=2.

Let n≥3. We divide the proof of Theorem 1.1 into the following four cases.

At first, we prove that

(1)

which is equivalent to

(2)

For this purpose, we construct an auxiliary function f(x)for x>3 by

Case 3. 5≤ n≤7. One has

(3)

where

We have

min{-s1,-2s4}>-(s1+2s4)

(4)

and

(5)

It follows from (3)～(5) and the isosceles triangle principle[6]that

Hence H2(Sn) is not an integer if 5≤n≤7.

Case 4. n=3 and 4. In this case, we can directly calculate the value of H2(Sn).

We have

That is, both H2(S3)and H2(S4)are not integers. Hence Theorem 1.1 is true when n=3 and 4. This finishes the proof.