基于小波预处理及自适应权函数的非局部均值滤波算法

毛玉星,李 超,贾海威

(重庆大学 电气工程学院,重庆 400030)

1 引 言

图像去噪技术一直以来都是图像处理领域的热点与关键技术,目的是从含噪图像得到真实图像信息,退化模型如(1)所示,

Y=X+n

(1)

其中,Y是含噪图像矩阵,也可称为观测图像,X是真实图像矩阵,n为加性噪声,在本文假设n为加性高斯白噪声,即n～N(0,σ2).图像去噪的目的是由观测图像Y通过变换计算,最大程度的准确获得X.为了准确的获取真实图像,主要研究的空域滤波算法有均值滤波、高斯滤波、非局部均值滤波[1,2]、双边滤波[3]等,频域滤波算法有维纳滤波、傅里叶变换滤波、小波阈值滤波等[4,5].其中,非局部均值滤波(NLM)因良好的去噪效果受到了广泛关注,其充分利用图像的冗余信息,以欲消噪点为中心,在一定搜索范围内,以每一像素点与中心点的加权欧式距离大小为权重,对周围点加权求和来得到中心点.

非局部均值滤波算法的相关研究主要集中在两个方面:1)对算法速度的提升,因其在计算欧氏距离过程中,是点与点的计算与平移,存在大量的计算,时间较长.为了优化加速,引入积分图的思想,先将含噪图像偏移,并与原图做差分平方,作为图像的欧氏距离矩阵,再对其求积分得到积分矩阵[6-8].此时,计算任意两个邻域框的欧氏距离时,只需要以待复原点为中心的邻域框四个角点在积分矩阵中的值即可,大幅度缩短了计算时间,为实时处理提供了方法,但是该方法使用图像块的思想,不能根据图像的局部信息适时调整滤波参数,对于图像的去噪效果有一定影响;2)对算法去噪效果的提升,主要是中心点权重、邻域框尺寸、滤波平滑参数等的优化及自适应.对于中心像素的权重,在文献[9-11]中,作者分别使用斯坦无偏风险估计(SURE)、最大似然估计、James-Stein 中心收缩估计来确定中心点权重,相较于通常让中心点权重等于搜索范围内的最大权重或者直接令中心点权重为1,在去噪效果上有一定程度的改善,但是会增加运算的复杂度.对于邻域框的研究,主要是对图像边缘处邻域框尺寸的选择和非相关点的滤除,在文献[12,13]中,作者使用结构张量矩阵来表示图像纹理结构的复杂度,将其分级,不同复杂等级的像素点,使用不同大小的邻域框,在文献[14,15]中,根据不同的理论建立权重阈值,当搜索范围内匹配点的权重小于阈值的时候,则认为其为不相关点,使其权重为0.对于滤波平滑参数,一般认为其与图像的噪声方差成正比,但同时也与图像局部结构信息相关,在文献[16]中,作者使用SUSAN边缘检测理论,以边缘检测响应来修正原始平滑参数(通过噪声方差得到),提升滤波效果,在文献[17]中,由均方误差来评价去噪效果,建立关于平滑参数的函数,再通过黄金分割算法计算最佳平滑参数以使均方误差最小,达到自适应最佳平滑参数的目的.对于欧氏距离权函数,一般使用高斯权函数,有的研究中也使用矩形权函数[18],但现阶段对于高斯权函数和矩形权函数在非局部均值滤波中的区别和对去噪结果的影响,研究很少.此外,也有通过对图像进行预处理提升去噪效果的研究,在文献[19]中,作者提出使用两步去噪的方法,第一步用较小的平滑参数hbasic进行非局部均值滤波作为对图像的预处理,第二步用最佳平滑参数hfinal进行非局部均值滤波,能够较准确的得到去噪图像,虽然该方法能够提高去噪效果,但是耗时长,且会在第一步处理时对图像边缘产生平滑.

通过上述分析,本文提出使用小波阈值去噪作为非局部均值滤波的预处理,然后用自适应欧氏距离权函数的非局部均值滤波进行去噪.后续章节分布如下:第二部分对非局部均值滤波算法作了简单回顾,第三部分引入适用于预处理的小波阈值去噪方法,第四部分探究了欧氏距离权函数与图像噪声强度以及局部结构的关系,提出自适应权函数选择方法,第五部分对本文所提方法进行实验仿真,第六部分对全文进行总结.

2 非局部均值滤波算法

含噪图像Y中任意像素点y(i,j),运用非局部均值滤波算法去噪得x(i,j),如公式(2)所示[6]:

(2)

其中,Ω为以y(i,j)为中心的图像二维搜索空间,y(p,q)为该空间内与y(i,j)不重合的任意点.W(i,j,p,q)为y(p,q)的权重,计算公式如公式(3)所示,w(i,j)为y(i,j)的权重,一般选用搜索框范围内的最大权重,z为归一化参数,计算如公式(4)所示.

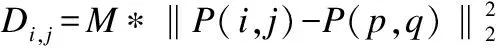
(3)

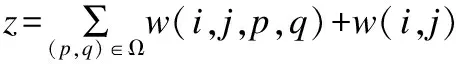
(4)

其中,M为一个二维的权函数,一般使用高斯权函数或者矩形权函数,*为卷积运算,‖·‖2为L2范数,P(i,j)和P(p,q)是指以y(i,j)和y(p,q)为中心的邻域块,也叫相似框.Di,j为相似框欧式距离矩阵与M的卷积,即加权欧式距离,h为滤波平滑参数.

3 小波阈值去噪预处理

小波分析作为信号处理的工具,是继Fourier分析之后又一有效的时频分析方法,可同时进行时域和频域分析,且有时域局部化和多分辨率特性,最早由Weaver将小波变换用于图像降噪[4].所谓的小波阈值降噪就是先将图像进行小波分解,再将小波系数的幅值同一个阈值进行比较,若小波系数的幅值比这个阈值小,则把小波系数置为0,若这个幅值比小波阈值大,则把小波系数进行保留和修改,最后将小波系数进行重构得到去噪图像[20,21].

小波阈值去噪分为硬阈值法和软阈值法,分别如公式(5)、(6)所示.

(5)

(6)

式中,T为阈值,y为含噪图像的小波变换系数,sgn(y)表示y的符号,Thard、Tsoft分别为硬阈值法滤波和软阈值法滤波的收缩函数.因为软阈值法中小波系数的幅值被减去了一部分,因此软阈值滤波中小波参数的估计是有偏的,滤波后的信号会过于平滑,丢失图像细节信息.因此,在本文中使用硬阈值法进行滤波,使用统一阈值Tuniv,如公式(7)所示.

(7)

式中,σn为零均值加性高斯白噪声的标准差,可由小波变换系数估计,如公式(8)所示,N为小波系数的总个数.

(8)

本文中,使用小波阈值去噪的目的是为非局部均值滤波进行预处理,即在频域滤除一部分噪声,来提高NLM的效果,所以在小波去噪时要尽可能的保留图像的结构以及边缘信息.通过测试,使用小波基函数sym8在预处理中有最好的表现.此处使用分辨率为256*256,噪声标准差σ=25的8位cameraman灰度图,对图像单层小波分解与双层分解的阈值去噪结果进行对比,如图1所示.由图可知,双层分解去噪能够获得更好的去噪效果,但是图像更加模糊,滤除了大量的结构信息,这必然会对后续步骤中的NLM带来不利影响,因此,本文使用单层分解硬阈值小波去噪进行预处理.

图1 小波阈值去噪结果Fig.1 Wavelet threshold denoising

4 自适应权函数的研究

在进行两个邻域块P(i,j)和P(p,q)的加权欧式距离计算时,一般使用高斯权函数模板与所得欧氏距离矩阵卷积求和[1,2].然而,研究发现,在高噪声的图像和低噪声的图像平滑区域使用矩形权函数模板能够取得更好的去噪效果,因此,有的研究中直接使用矩形权函数[6],但是对于权函数的自适应选择研究较少.权函数模板与相似框有一样的尺寸,高斯权函数和矩形权函数的计算公式分别见公式(9)与(10).

(9)

K(i,j)=1/(2p+1)2

(10)

式中,α为高斯权函数标准差,p为相似框半径.由公式(9)可知,权函数标准差越小,计算所得高斯模板中心点的值越大,即在加权欧氏距离计算中,中心点所占权重越大;而当权函数标准差越大,高斯模板中各数值相差越小,直到所有值趋于相等,变成公式(10)计算的矩形模板.在传统NLM中对高斯和矩形模板的选择,以及高斯权函数标准差的选择一般由经验随机选择,且一旦选择之后,对整幅图的每一个像素点都是采用相同的权函数.但是在去噪过程中,因图像纹理结构以及含噪强度的不同,相似框欧式距离计算时中心点的权重占比应该有所区别.本文以灰度图为例分析,对无噪图像,两个像素点相似性判断只计算这两个点的欧式距离即可,即相似框的中心点权重为1,周围点权重全为0,而当图像噪声强度越大,则越依赖相似框中周围点的欧氏距离来辅助判断,中心点的权重越小.因此,在噪声强度低时,应使用标准差较小的高斯模板,随着噪声增加,高斯权函数标准差增大,以加大相似框中非中心点的权重,直到权函数模板趋于矩形模板,此时,相似框中所有像素点的权重相等.对图像局部而言,在低频平坦区,相似框中每个点灰度值相差不大,所有点的权重应该相近,使用矩形模板较好,而在高频边缘区,中心点与周围点的灰度值相差较大,应该减小周围点权重,使用标准差较小的高斯权函数模板.

4.1 图像局部分析

由上述分析可知,权函数的使用与图像局部纹理结构有关.为了更加准确的描述图像的局部纹理复杂度,本文使用线性结构张量对其进行分类[12],线性结构张量由初始结构张量与高斯核函数卷积得到,如公式(11)所示.

(11)

其中Gδ为标准差为δ的高斯核函数,Ix、Iy分别为图像水平方向与垂直方向的梯度.对公式(11)进行矩阵变换,可求得法线方向特征值λ1和切线方向特征值λ2如公式(12)所示.

(12)

定义λ=|λ1(i,j)-λ2(i,j)|,λ(i,j)越大,则该点灰度变化越剧烈,反之,则图像该点处越平坦.可据此将图像的纹理复杂度分为4级,并根据不同的等级使用不同的权函数M,如公式(13)所示,K(f)表示半径为f的矩形模板,G(α,f)表示标准差为α,半径为f的高斯模板.

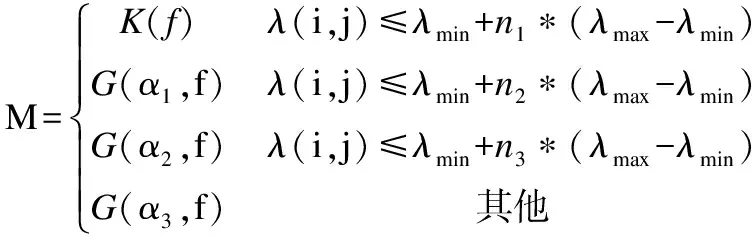
(13)

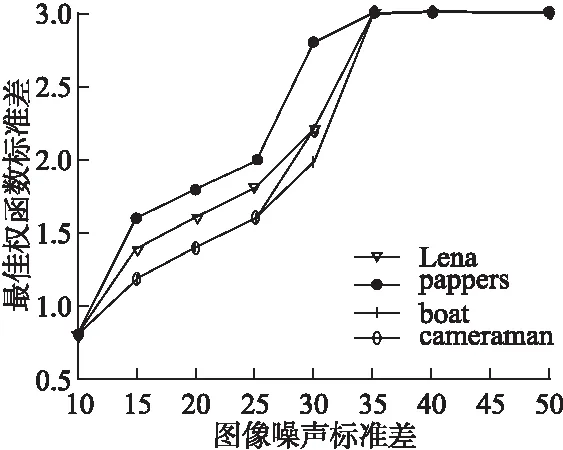
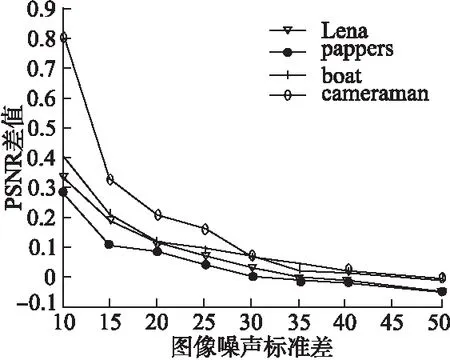
其中,α1>α2>α3,n1

4.2 图像整体分析

由上述分析可知,权函数的选择与图像噪声强度相关.通过实验发现,当使用高斯权函数且当α>3时,与使用矩形权函数去噪的峰值信噪比(PSNR)相近,即高斯权函数模板近似为矩形权函数模板.本文分别对预处理之后的Lena图、Peppers图、boat图和cameraman图进行实验,探究图像噪声强度与权函数的关系,以及在不同噪声情况下的最佳高斯权函数标准差α.使用高斯权函数进行测试,权函数标准差间隔0.2,从0.6一直到3,取不同噪声强度时最佳权函数标准差如图2所示,从图中可以看出,在图像噪声σ≥35时高斯权函数最佳标准差稳定在最大值3,此时高斯模板近似为矩形模板.然后,为了探究高斯权函数与矩形权函数的适用范围,将不同噪声情况下使用高斯权函数去噪的最佳PSNR和使用矩形权函数去噪的PSNR做差如图3所示,由图可知,图像含噪越少,使用高斯权函数效果越优于矩形权函数,在图像噪声标准差为10时,cameraman图使用高斯权函数去噪的PSNR比使用矩形权函数高0.8dB.随着噪声强度变大,曲线趋于负,结合图2分析,之所以负值时幅值较小是因为高斯权函数标准差为3,此时的高斯模板已近似为矩形模板,故高噪声时使用矩形权函数效果更优.综上,当σ≥35时,使用矩形权函数,σ<35时,使用高斯权函数,且标准差设置为α=(0.08～0.1)×σ,α1=α,α2=0.8×α,α3=0.6×α往往能够取得最好的去噪效果,此处取n1为0.05,n2为0.3,n3为0.6.

图2 权函数最佳标准差与图像噪声关系Fig.2 Relationship between the kernel function′s optimal standard deviation and the image′s noise level

图3 两种权函数PSNR差值与图像噪声关系Fig.3 Relationship between the difference of PSNR calculated by two different kernel function and the image′s noise level

综上分析可知,本文对一幅图像使用非局部均值去噪步骤如下:1)估计图像噪声方差,可由公式(8)估计,本文假设图像噪声方差已知;2)对图像进行小波单层硬阈值去噪预处理;3)根据噪声强度自适应选择权函数对预处理之后的图像非局部均值滤波,权函数选择如公式(14)所示,G表示高斯权函数,K表示矩形权函数,当选择G,再结合公式(13)根据局部结构自适应设置高斯权函数标准差.

(14)

5 仿真与实验分析

本文在matlab环境中使用C语言编程进行仿真,选取搜索框尺寸S=21×21,相似框尺寸P=5×5,滤波参数h从0.6*σ到σ间距0.5取每次实验最佳的PSNR,原始NLM中高斯权函数标准差随机选取1.4.为了验证本文中小波预处理以及自适应权函数各自的作用,以Lena图和Peppers图为例,在不同噪声强度下,对比文献[1]中原始NLM、小波预处理之后分别使用高斯权函数和矩形权函数以及本文自适应权函数进行非局部均值滤波的PSNR见图4.其中,2-G、2-K分别表示小波预处理之后使用高斯权函数和矩形权函数进行非局部均值滤波,高斯权函数的标准差选择1.4.对比2-G和文献[1],可以看出小波预处理对去噪结果的PSNR提高很大,在σ=35时,对Peppers图高达0.7dB,且随着噪声强度变大,有进一步提高的趋势;对比2-G和2-K曲线可以发现,噪声低时使用高斯权函数效果优于使用矩形权函数,而当噪声强度大时,使用矩形权函数有更好的去噪效果,验证了根据不同噪声强度选用不同的权函数的必要.本文的自适应权函数结合了2-G和2-K两种权函数的优点,而本文方法在低噪声时效果优于2-G是因为本文方法根据噪声强度和图像纹理结构,自适应确定高斯权函数的标准差.

图4 使用不同去噪方法的峰值信噪比(左边Lena图、右边Peppers图)Fig.4 PSNR comparison with different method(Left is Lena,right is Peppers)

表1 不同方法去噪的峰值信噪比(分贝)
Table 1 PSNR results of various methods(dB)

σ1520253035405060Lena 256∗256噪声图24.692922.293420.374418.90417.651616.569914.82413.4823文献131.372729.771628.418827.370726.344125.432824.002422.7428文献1931.098730.036528.968527.468926.532725.645524.499823.2198本文方法31.581630.170929.073528.090627.225726.319425.185124.0877Peppers 256∗256噪声图24.664822.261220.33118.752117.479516.459314.689813.3302文献131.857430.2628.872727.533326.530225.609924.186622.8341文献1931.572730.54929.571927.881626.946925.980224.779123.4415本文方法32.185230.851229.647428.456827.557226.738325.538524.2277

图5 不同方法的消噪图对比,(a)、(b)、(c)、(d)、(e)分别是原图、噪声图(Lena、Peppers噪声标准差分别为20、25)、原始NLM方法去噪图、文献[19]两步去噪图、本文方法去噪图Fig.5 Filtering performance of various denoising method(a)Oringal Image(b)Noisy Image,Lena′s σ=20,Peppers′s σ=25(c)Oringal NLM(d)Two Stage Method[19](e)Our Method

将两种图像运用不同方法去噪的PSNR统计如表1所示.从表中数据分析可知,相较于前两种方法,本文方法有更高的PSNR,在噪声强度越大时,提升效果越明显,与原始NLM相比,PSNR最高有1.4dB的提升.将Lena图 =20,Peppers图=25时运用不同方法去噪的效果图展示如图5,其中图5(a)为原图、图5(b)为噪声图、图5(c)为原始NLM效果图、图5(d)为文献[19]方法的效果图、图5(e)为本文方法消噪效果图.从图5可以看出,运用本文方法进行去噪,在图像边缘轮廓等细节处有更好的视觉效果.原因是对相同噪声强度的图像,经过小波预处理,在进行非局部均值滤波时相比于原始NLM选择的最佳平滑参数更小,即图像平滑程度更低,且本文根据图像边缘结构自适应选择权函数,能更好的保留边缘结构.

表2 不同去噪方法时间(秒)
Table 2 Time consumption of different method(s)

NLM文献[19]本文方法256∗25663.93s127.66s64.93s512∗512253.25s509.77s258.9s

将不同分辨率的Lena含噪图运用不同去噪方法的时间对比如表2所示,从表中可以看出,本文相比于文献[19]中两步滤波方法,同样进行了预处理,但是时间节省了近一半,相比于原始算法,本文方法在时间增加很少的情况下,提高了去噪的效果.

6 总 结

通过对非局部均值滤波和小波阈值去噪的分析,本文提出将非局部均值滤波与小波去噪有效结合的方法,对一幅含噪图像首先通过小波阈值去噪预处理,再使用非局部均值滤波.这种方法可以在不需要优化非局部均值滤波参数的情况下,一定程度的提高去噪效果,图像噪声强度越大时提升越明显,且相对于其他预处理方式,使用小波预处理可以更好的保存图像边缘等结构信息.此外,本文对非局部均值滤波的欧氏距离权函数进行了研究,发现在低噪声图像的高频边缘区使用高斯权函数,高噪声图像和低噪声图像的平坦区使用矩形权函数相较于原始算法有更好的去噪效果,提出基于图像噪声强度与纹理结构的自适应权函数非局部均值滤波.最后,经过仿真对比验证,本文方法有更高的峰值信噪比和更好的视觉效果.