曲线裂纹裂尖SIFs 等效分析的 广义参数Williams 单元确定方法

徐 华，邓 鹏，蓝淞耀，刘祖容，杨绿峰,2

(1.广西大学土木建筑工程学院，工程防灾与结构安全教育部重点实验室，广西防灾减灾与工程安全重点实验室，广西，南宁 530004； 2.广西壮族自治区住房和城乡建设厅，广西，南宁 530028)

当前线弹性平面断裂力学研究领域中，主要围绕直线裂纹的开裂模式、扩展和相关断裂参数等开展研究。然而，裂纹在扩展过程中裂尖合力方向可能发生变化，导致扩展角变化，即使初始裂纹为直线型，绝大部分经扩展后的裂纹最终都以曲线的型式存在，因而曲线裂纹更符合实际工程。曲线裂纹具有非线性裂纹边界条件，与直线裂纹的线性裂纹边界条件相比，其求解难度更高。因而，研究曲线裂纹的相关断裂参数及开裂机理意义大、难度高。

SIFs 作为表征裂尖附近应力-应变场强弱程度的重要参量，是目前裂纹问题的重点研究对象。近年来，国内外多个课题组对曲线裂纹裂尖SIFs 开展了研究，其分析方法主要归纳为半解析法、解析法和数值法三大类。半解析法在曲线裂纹的分析中有着较广泛的应用，通常将问题转化为奇异积分方程进行求解：Nik Long 等[1]提出将复变函数多重弯曲裂纹问题转化为超奇异积分方程，并通过双圆弧裂纹裂尖SIFs 求解的算例证明了该方法的正确性；Aridi 等[2]根据该方法求解了直裂纹与曲裂纹相互作用情况下的裂尖SIFs；Elfakhakhre 等[3]采用修正的复势自由牵引边界条件，将半平面弹性弯曲裂纹问题转化为奇异积分方程对裂尖SIFs 进行求解；Monfared 等[4]则基于位错技术，导出了非均匀平面上多条弯曲裂纹的I 型和II 型SIFs 求解的Cauchy奇异积分方程。在解析法方面，一些研究者结合复变函数和保角映射理论，分析了多种典型的幂函数曲线裂纹，其中：胡元太等[5]利用Stroh 法及映射法研究了沿抛物线分布的各向异性曲线裂纹问题，但只适用于较平坦的抛物线；魏雪霞等[6]依据复变函数和保角映射推导新的保角变换公式，得到了对称抛物线曲线裂纹问题的I 型SIFs 解析解；郭怀民 等[7]将魏雪霞的方法推广至3 次～6 次幂函数类对称曲线裂纹的裂尖SIFs 求解。数值法则是目前曲线裂纹问题分析的主流方法，其优点在于能够模拟各种复杂边界，适用范围广，当前最常用的是边界元法和有限元法：王银邦等[8]采用边界元法研究了含曲线裂纹圆柱的扭转问题，同课题组陆孜子等[9]将研究对象扩展至含曲线裂纹的任意柱体；Elangovan等[10]利用有限元法给出了非加劲弯曲板的裂尖SIFs；Judt 等[11]基于有限单元法改进了路径无关积分法并精确计算出曲线裂纹尖端SIFs；Choi 等[12]提出了曲线裂纹中SIFs 分析的等几何法，与标准有限元方法相比，相互作用积分域具有更高的应力-应变场连续性。综上所述，解析法和半解析法均适用范围较小且理论推导复杂；而数值法具有广泛的适用性，其中边界元法和有限元法在曲线裂纹问题的分析中虽然最常见，但二者均需通过复杂的后处理获取SIFs，由此导致二次误差。杨绿峰等[13]提出的W 单元以SIFs 为基本未知量进行求解，既继承有限元法的通用性，又避免后处理引入的人为误差，且精度高，在断裂分析中优势明显；同课题组徐华等[14]在前期研究成果上提出了W 单元与矩阵压缩相结合的SIFs 快速解法，该方法能够提高复杂荷载作用下带裂纹薄板裂尖SIFs 的求解效率，且有较高的计算精度，但W 单元应用于裂纹问题分析时，裂纹面须满足σθ=0、τρθ=0(θ=±π)，而曲线裂纹在直接利用其求解时不能满足该边界条件。

为克服上述缺陷，本文在裂尖附近截取斜率呈单调变化的曲线微段，以该曲线微段两端点的距离为半径，并以裂尖为圆心建立等效区。在截取裂纹微段两端引切线并交叉成折线段，以该折线段近似代替曲线微段，则该折线与裂尖相连的一段处于θ=±π 上。经此改进，裂尖局部满足裂纹面自由的边界条件，即σθ=0、τρθ=0(θ=±π)。本文重点研究裂尖等效区的选取，并通过算例分析证明曲线裂纹尖端局部等效原则的合理性。

1 曲线裂纹尖端等效区计算格式

1.1 裂尖曲线段等效处理

在平面任意位置建立整体坐标系XOY，曲线裂纹可用曲线函数Y=H(X)表示。如图1 所示，在裂尖处建立局部直角坐标系xoy和极坐标系ρθ：直角坐标系以o为原点，沿o点切线裂尖指向方向为x轴正方向，其逆时针旋转90°为y轴；极坐标系以o为极点，ox为极轴ρ，逆时针旋转方向为正方向。局部坐标系x轴与整体坐标系X轴所成角度为γ。设裂尖o在整体坐标系下的坐标为(X0,Y0)，整体坐标系与局部坐标系的坐标转换关系如下：

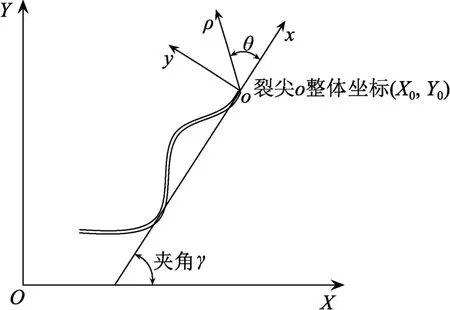
图1 曲线裂纹整体坐标系和裂尖局部坐标系 Fig.1 The global coordinate of curved crack and local coordinate of crack tip

图2 曲线裂纹裂尖局部等效区 Fig.2 The local equivalent region of curved crack tip

如图2 所示，在裂尖附近微小区域截取斜率呈单调变化的裂纹曲线微段ΓA，其截取处裂纹上下表面分别用点A1和A2表示。分别在A1、A2处作切线，并与x轴分别交于点B1、B2，令∠A1B1o=∠A2B2o=ψ。取点A1、A2的局部极坐标为(ρA,θA)，线段oB1、oB2的长度为ρB。以ψmin为临界值，当ψ≥ψmin时，ΓA的曲率足够小，此时可对ΓA进行等效替换并建立等效区：

1) 以o点为圆心，ρB为半径建立圆形区域ΩB，称为等效奇异区，线段oB1、oB2分别为裂纹上下表面。根据角度区间(-π, π)将奇异区均等分为p个相同的扇形条元，如图2 所示，p=8；

2) 以o点为圆心，ρB为内径，ρA为外径，建立圆环区域ΩA，称为等效常规区，该区域以线段A1B1和A2B2近似等效原裂纹的上下表面，并同样离散为p个常规单元，除裂纹上下表面连接的2 个单元外，其余p-2 个单元形状大小均相同；

3) ΩA+ΩB合称为曲线等效区。

由于等效区尺寸很小，在等效区内对曲线进行等效处理时，因线段A1B1和A2B2在点A1、A2处与裂纹曲线相切，线段oB1、oB2是在点o处与裂纹曲线相切，故用折线A1B1o和A2B2o拟合ΓA可保证较高的拟合度，并能保证等效奇异区裂纹面自由的边界条件，即σθ=0、τρθ=0(θ=±π)。

根据等效常规区单元划分规则可知：∠A1oB1应小于扇形条元弧心角，即∠A1oB1＜2π/p。因曲线微段ΓA足够小，可近似看作圆弧，则有∠oA1B1=∠A1oB1=｜θA-π｜。根据几何关系，综合等效区建立规则，得到如下关系式：

综上所述，曲线微段截断点A1(A2)可按下列原则确定：

1) 曲线微段ΓA的斜率呈单调变化；

2)θA满足式(3)的要求。

确定点A1(A2)后，即可通过点A1(A2)与圆心o建立裂尖曲线等效区。根据式(4)，通过点A1(A2)的局部极坐标(ρA,θA)，便可确定等效奇异区ΩB的半径ρB，进而确定等效常规区和等效奇异区的范围。

1.2 等效奇异区Williams 级数位移场与SIFs

按W 单元离散规则对ΩB区域进行网格离散，如图3 所示。以裂尖o为圆心，α(0＜α＜1)为比例分别建立半径为αρ B,α2ρB, ···,α nρB的n个同心圆，将各条元分为裂尖扇形微单元和n层相似子单元，即W 单元，其最外层单元中的一条边与常规区相连，称之过渡单元。

忽略裂尖扇形微单元的刚度贡献，在W 单元内根据平面断裂分析的Williams 级数[15]位移场表达式，对其位移场进行改进并截取级数的前m+1项，如式(5)所示：

图3 裂尖等效奇异区网格离散 Fig.3 Discretization of equivalent singular region at crack tip

式中：u、v分别表示x、y坐标方向的位移分量；ai、bi分别表示待定系数，因无特定物理意义，称为广义参数，其值由外荷载与边界条件确定；

fi,11(θ) ,fi,12(θ) ,fi,21(θ) ,fi,22(θ)为三角函数，详见文献[13]。

待定系数a1、b1分别对应位移表达式中的ρ1/2项和应力表达式中的ρ-1/2项，同I、II 型SIFs 有如下关系：

整理式(5)，将其改为矩阵形式如下：

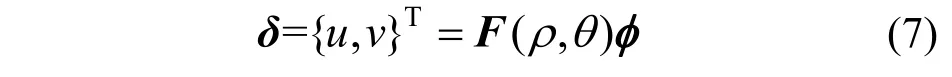
式中：δ表示整体位移场；φ表示广义参数，且有：

1.3 等效奇异区整体刚度方程集成

根据有限元中8 节点等参数单元理论，利用变分原理建立奇异区条元内任意子单元刚度方程：

根据式(5)可得：

式中：()kT为第k层子单元转换矩阵，且：

将式(11)代入式(10)，并在等式两边左乘T(k)T

可得：

整理后得广义刚度方程：

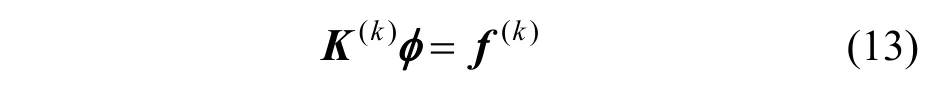
式中：K(k)表示第k层子单元广义刚度矩阵；f(k)表示第k层子单元广义荷载列阵，因奇异区内不存在外荷载，故f(k)=0。

根据式(13)可知，第2 层到第n层子单元刚度方程存在相同乘子φ，故可叠加如下：

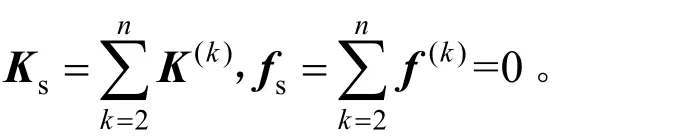
扇形条元最外层的过渡单元，有3 个节点位于等效常规区与等效奇异区的边界上，剩余5 个节点位于等效奇异区内，根据节点所处区域的不同，将过渡单元刚度方程进行分块并与式(14)叠加，即可得到整个条元的刚度方程如下：

根据式(15)集成所有条元刚度方程，即等效奇异区刚度方程，分块表示如下：

2 总刚度方程的集成与SIFs 求解

将所有常规单元刚度集成并区分出等效奇异区边界上的2p+1 个节点，将刚度方程分块如下：

叠加式(16)与式(17)得到总刚度方程如下所示：

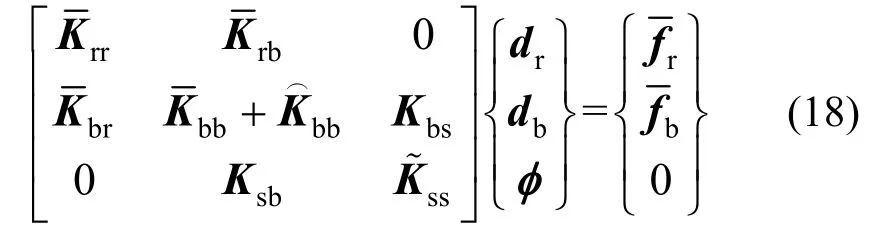
3 算例分析

例1. 含中心圆弧裂纹薄板，以板中心为原点建立整体坐标系XOY，并在各裂尖分别建立局部坐标系，如图4 所示。取H和W远大于圆弧R，即为无限大板，板厚t=1 cm。圆弧半径为R，弧心角为2β，关于Y轴对称，弹性模量20.0 GPa，泊松比μ=0.167；该板受双向拉伸荷载作用， 荷载大小为σ=1 kN/cm2。结合本文等效处理原则和W 单元求解该算例中裂尖SIFs，并与ANSYS 中1/4 奇异单元计算结果和应力强度因子手册[16]的解析解作比较。W 单元模型的等效奇异区网格离散如图3 所示，取条元划分个数p=8；1/4 奇异单元模型的奇异区取周向离散单元数为8，其单元大小和数目与W 单元相同；两种计算模型的常规区均通过ANSYS 进行网格自由离散，单元数均控制在500 个左右。

本算例中，W 单元的3 个重要参数α，m和n取参考值[13]：α=0.95，m=20，n=300。

由应力强度因子手册可知，含有中心圆弧裂纹无限大板的SIFs 解析解为：

图4 含中心圆弧裂纹无限大板 Fig.4 Infiniteplate with central arc crack

1) 在R与β取不同值的情况下，通过改变ψ选取不同大小的等效奇异区，计算A裂尖SIFs，并与解析解作比较，分析ψ对SIFs 的影响。

图5 和图6 所示，当R与β取不同值时，本文方法的SIFs 随ψ变化的计算结果，所有计算结果与解析解的误差均在5%以内，说明ψ的取值在(13π/18, 35π/36)区间均能得到正确结果。在(13π/18, 5π/6)区间内，随着ψ增大，KI呈递减趋势，KII呈递增趋势，且二者均趋近于解析解；在(5π/6, 8π/9)区间内，KI、KII最接近解析解，误差小于1%；当ψ＞8π/9 时，等效区的尺寸过小，W 单元在奇异区尺 寸过小的情况下误差会增大。综上所述，给出建议值ψmin=5π/6，且奇异区尺寸不宜过小，建议等效区截取曲线长度大于原曲线长度的1/5。

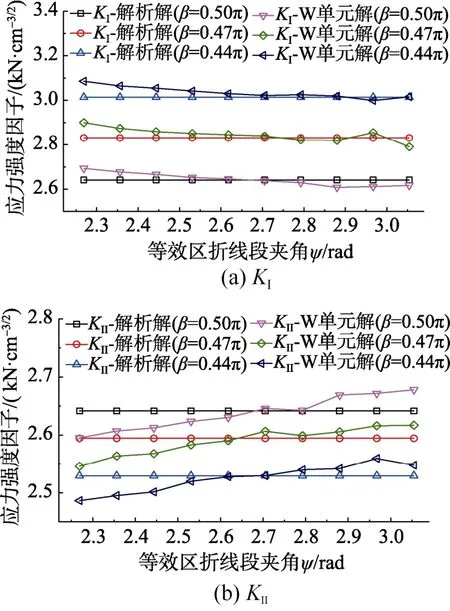
图5 不同β 情况SIFs 随ψ 变化的计算结果(R=10 cm) Fig.5 Calculation of SIFs with ψ changed under different β conditions (R=10 cm)

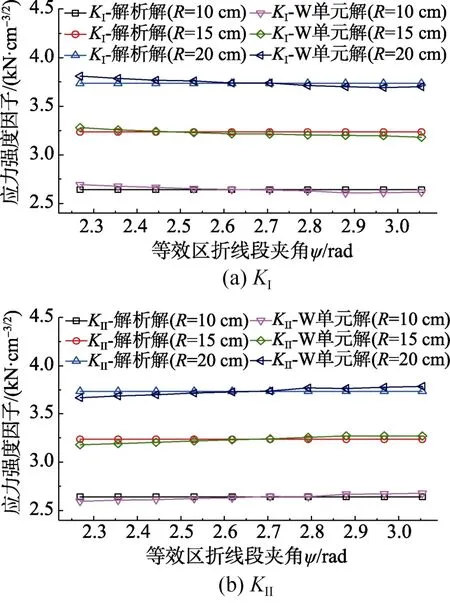
图6 不同R 情况SIFs 随ψ 变化的计算结果(β=π/2) Fig.6 Calculation of SIFs with ψ changed under different R conditions(β=π/2)

2) 根据建议，取ψ=5π/6，分别计算不同R、β情况下A裂尖的SIFs，并与ANSYS 计算结果和解析解进行比较，计算结果如图7 和图8 所示。

本文方法结果与解析解非常吻合，最大误差为1.32%，而ANSYS 的1/4 奇异单元计算结果最大误差为2.77%。由图7 可知，当R=10 cm，β在(π/18, 4π/9)区间递增时，KI先增大后减小，在β=π/4 时最大，KII呈递增趋势；由图8 可知，当β=π/6 时，随着R的增大，KI、KII都呈递增趋势。

图7 SIFs 随β 变化的计算结果(R=10 cm) Fig.7 Calculation of SIFs changing with β (R=10 cm)

图8 SIFs 随R 变化的计算结果(β=π/6) Fig.8 Calculation of SIFs changing with R(β=π/6)

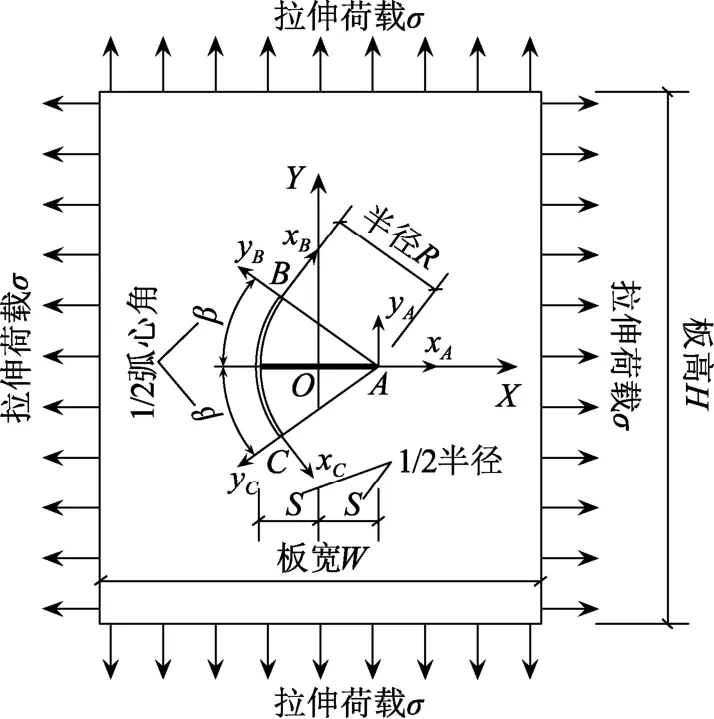
图9 含圆弧分岔裂纹无限大板 Fig.9 Infiniteplate with bifurcate arccrack

例2. 含圆弧分岔裂纹薄板，以板中心为原点，建立整体坐标系XOY，并在各裂尖分别建立局部坐标系，如图9 所示。取H和W远大于圆弧R，即为无 限大板，板厚t=1 cm。圆弧半径为R=2S，S为直线段裂纹半长，弧心角为2β，关于X轴对称，弹性模量20.0 GPa，泊松比μ=0.167；该板受双向拉伸荷载作用，荷载大小为σ=1 kN/cm2。结合本文等效处理原则和W 单元求解该算例中裂尖 SIFs，并与ANSYS中1/4奇异单元计算结果和应力强度因子手册[16]的解析解作比较。W 单元模型的等效奇异区网格离散如图3 所示，取条元划分个数p=8；1/4 奇异单元模型的奇异区取周向离散单元数为8，其单元大小和数目与W 单元相同；两种计算模型的常规区均通过ANSYS 进行网格自由离散，单元数均控制在500 个左右。

本算例中，等效区根据建议取值如下：β在(0, π/2)区间时，ψ=π-β/5；β在[π/2, π]区间时，ψ=π-β/10。W 单元的3 个重要参数α，m和n取参考值[13]：α=0.95，m=20，n=300。

由应力强度因子手册可知，含圆弧分岔裂纹无限大板的SIFs 解析解为：

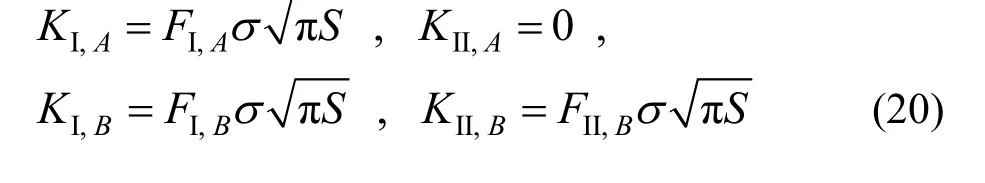
取S=10 cm，β=π/12～11π/12 计算各裂尖SIFs随β改变的变化趋势，并将W 单元计算结果与ANSYS 计算结果和解析解进行对比。

由于板受双向拉伸时，A裂尖裂纹上下表面无水平方向的相对位移，故KII始终为0，不进行图示，其余计算结果如图10 所示。对比KI,A和KI,B发现：W 单元计算结果和ANSYS 计算结果均与解析解非常吻合，排除值太小导致误差值偏大的情况，其余值中W 单元最大误差为2.34%，ANSYS 最大误差为3.32%；对比KII,B发现：W 单元计算结果比ANSYS 计算结果更吻合解析解，其中W 单元最大误差为1.89%，ANSYS 最大误差为3.94%，且在β=π/3～3π/4 区间ANSYS 误差明显大于W 单元；随着β的增大，KI,A先减小后增加，KI,B和KII,B绝对值先增加后减小，KI,A在β=2π/3 时最小，KI,B在β=5π/12 时最大，KII,B绝对值在β=7π/12 时最大。

图10 SIFs 随β 变化的计算结果(S=10 cm) Fig.10 Calculation of SIFs changing with β (S=10 cm)

4 结论

本文对曲线裂纹尖端局部区域进行等效处理并建立等效区，从而使曲线裂纹在裂尖等效奇异区内满足σθ=0、τρθ=0(θ=±π)的边界条件，结合等效处理原则与W 单元计算了含中心圆弧裂纹无限大板与含圆弧分岔裂纹无限大板的裂尖SIFs，证明了本文方法的合理性和正确性，得到结论如下：

(1)ψ的取值在(13π/18, 35π/36)区间与解析解的误差均在5%以内，证明了本文对裂尖进行等效处理的合理性。在(13π/18, 5π/6)区间内，随着ψ增大，KI呈递减趋势，KII呈递增趋势，且二者均趋近于解析解；在(5π/6, 8π/9)区间内，KI、KII误差小于1%；当ψ＞8π/9 时，等效区的尺寸过小，W 单元在奇异区尺寸过小的情况下误差会增大。综上所述，给出建议值ψmin=5π/6，且奇异区尺寸不宜过小，建议等效区截取曲线长度大于原曲线长度的1/5。

(2) 当奇异区尺寸取建议值时，本文方法在含中心圆弧裂纹无限大板裂尖SIFs 的计算中，计算结果与解析解的最大误差为1.32%，精度较ANSYS 计算结果更高；在含圆弧分岔裂纹无限大板裂尖SIFs 的计算结果中：W 单元和ANSYS 的KI,A、KI,B计算结果均与解析解非常吻合，除去值太小导致误差值偏大的情况，其余值中W 单元最大误差为2.34%，ANSYS 最大误差为3.32%；W 单元的KII,B计算结果比ANSYS 更吻合解析解，其中W 单元最大误差为1.89%，ANSYS 最大误差为3.94%，且在β=π/3～3π/4 区间ANSYS 误差明显大于W 单元。算例结果证明，本文方法具有高精性和广泛的适用性。

(3) 含中心圆弧裂纹无限大板受双向拉伸时，R不变，随着β在(π/18, 4π/9)区间递增，KI先增大后减小，在β=π/4 时最大，KII呈递增趋势；当β不变时，随着R的增大，KI、KII都呈递增趋势。

(4) 含圆弧分岔裂纹无限大板受双向拉伸时，C不变，随着β在(π/12, 11π/12)区间递增，KI,A先减小后增加，在β=2π/3 时最小；KI,B和KII,B绝对值先增加后减小，KI,B在β=5π/12 时最大，KII,B绝对值在β=7π/12 时最大。