含缺陷矿用圆环链裂尖应力应变对材料力学参量的敏感性分析

樊亚玲，杨宏亮

1西安铁路职业技术学院机电工程学院 陕西西安 710014

2西安科技大学工程训练中心 陕西西安 710054

矿 用圆环链是刮板输送机、刨煤机及滚筒采煤机等矿山设备的主要牵引部件之一[1]。矿用圆环链在编环过程中，由于弯曲工艺会引起材料加工硬化，加工硬化程度不同，会使其力学参量发生变化，进而影响裂纹尖端应力应变场和断裂规律。圆环链在制造过程中产生的加工硬化提高了材料屈服强度和极限拉伸强度[2]。加工硬化减小了材料的硬化系数，材料硬化指数也随着加工硬化程度的增大而减小[3]。材料力学参量对圆环链断裂过程中所起的作用不同，圆环链裂纹尖端应力应变也对材料力学参量的敏感性不同。为了更清楚了解含缺陷矿用圆环链的断裂规律，以矿用φ18×64 C 级圆环链为例，利用 ABAQUS 软件分析了圆环链弯曲过程中裂纹尖端应力应变对材料力学参量的敏感性。

1 理论分析

研究裂纹时采用紧凑拉伸试样 (1T-CT)，试样几何尺寸符合 ASTM E399—90 标准，裂纹长度a＝2 mm，宽度b＝2 μm。在有限元模拟过程中，取裂尖应力强度因子K＝30 MPa·m0.5。分析选用矿用φ18×64 C 级圆环链，材质为 23MnNiCrMo54。由于加工硬化特性，其力学模型符合 Ramberg -Osgood 关系[4]，因此，在有限元模拟计算过程中选取R-O关系，其表达式为

式中：ε、σ分别为真实应变和真实应力；E为弹性模量，取E＝210 GPa[5]；α为偏移系数，取α＝1；σ0为屈服强度，取σ0＝1 166 MPa；n为硬化指数，取n＝4.5。

材料的每个力学参量对裂尖应力应变的敏感性不同。为了分析裂尖应力应变对材料力学参量的敏感性，定义因变量Y对自变量X变化的敏感性系数

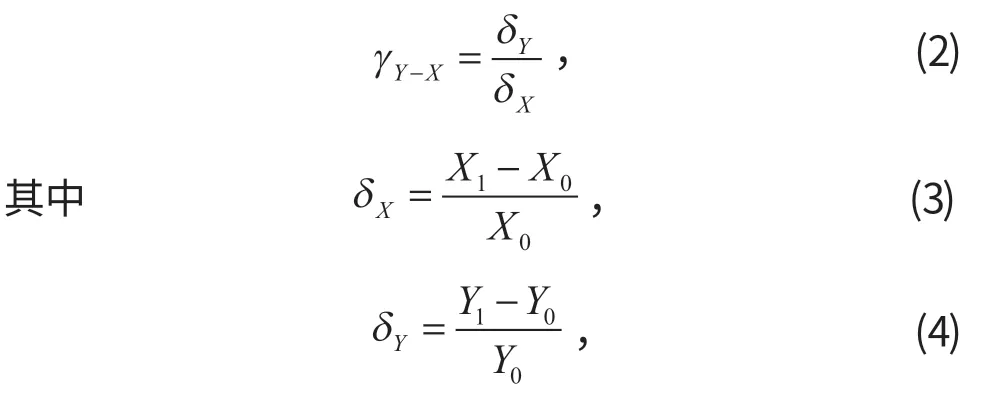
式中：X1、X0为自变量；δ X为自变量相对于初值X0时的变化幅度；δY为自变量X变化后因变量Y的变化幅度。

敏感系数γ≥1，表示因变量变化幅度大于自变量变化幅度，裂尖应力应变对材料力学参量比较敏感，受材料力学参量的影响较大；敏感系数γ＜1，表示因变量变化幅度小于自变量变化幅度，裂尖应力应变对材料的力学参量不敏感。

2 敏感性分析

2.1 对屈服强度的敏感性

裂尖 Mises 应力对屈服强度敏感性的影响如图 1所示。由图 1 可知，材料屈服强度越大，Mises 应力对屈服强度的敏感性越小，并且离裂尖越远，敏感系数越小。在离裂尖最近处敏感系数γMises-σ0<1，说明Mises 应力对材料屈服强度不敏感，裂尖 Mises 应力的变化幅度小于材料屈服强度的变化幅度。当裂尖距离较小时，裂尖的 Mises 应力对材料的屈服强度的敏感性随着屈服强度的增大而减小[6]。

图1 Mises 应力对屈服强度的敏感性Fig.1 Sensitivity of Mises stress to yield strength

裂尖等效塑性应变对屈服强度变化的敏感性如图 2 所示。由图 2 可以看出，敏感系数为负值，说明裂尖等效塑性应变和材料的屈服强度负相关，材料的屈服强度增大时，裂尖等效塑性应变减小。从敏感系数的绝对值来看，裂尖等效塑性应变对材料屈服强度的敏感性随着材料屈服强度的增大而减小；离裂尖越远，敏感系数的绝对值越大，等效塑性应变对材料的屈服强度越敏感。当材料屈服强度为初始值的 0.8倍，并且离裂尖较远时，敏感系数绝对值的最大值可达 3，表示裂尖等效塑性应变变化幅度大于材料屈服强度的变化幅度，说明裂尖等效塑性应变对材料的屈服强度很敏感。

图2 等效塑性应变对屈服强度的敏感性Fig.2 Sensitivity of equivalent plastic strain to yield strength

2.2 对弹性模量的敏感性

裂尖 Mises 应力对材料弹性模量敏感性的影响如图 3 所示。由图 3 可以看出，当离裂尖非常近时，Mises 应力和材料弹性模量正相关，材料弹性模量增大，敏感系数减小；裂尖距离增大时，Mises 应力和材料弹性模量负相关。从敏感系数的绝对值看，当r≤0.7 mm 时，弹性模量越大，敏感系数越大，Mises应力对材料弹性模量的敏感性越大；当r＞0.7 mm时，弹性模量越大，敏感系数越小，Mises 应力对材料弹性模量的敏感性越小。

图3 Mises 应力对弹性模量的敏感性Fig.3 Sensitivity of Mises stress to elastic modulus

等效塑性应变对弹性模量变化的敏感性如图 4 所示。由图 4 可以看出，裂尖等效塑性应变与材料的弹性模量负相关，材料的弹性模量越大，敏感系数的绝对值越小，敏感性变小；随着裂尖距离的增大，等效塑性应变对弹性模量的敏感性增大，弹性模量越大，敏感系数增大的幅度越小。裂尖等效塑性应变对材料的弹性模量较为敏感，随着裂尖距离的增大，裂尖等效塑性应变的变化幅度大于材料弹性模量的变化幅度。

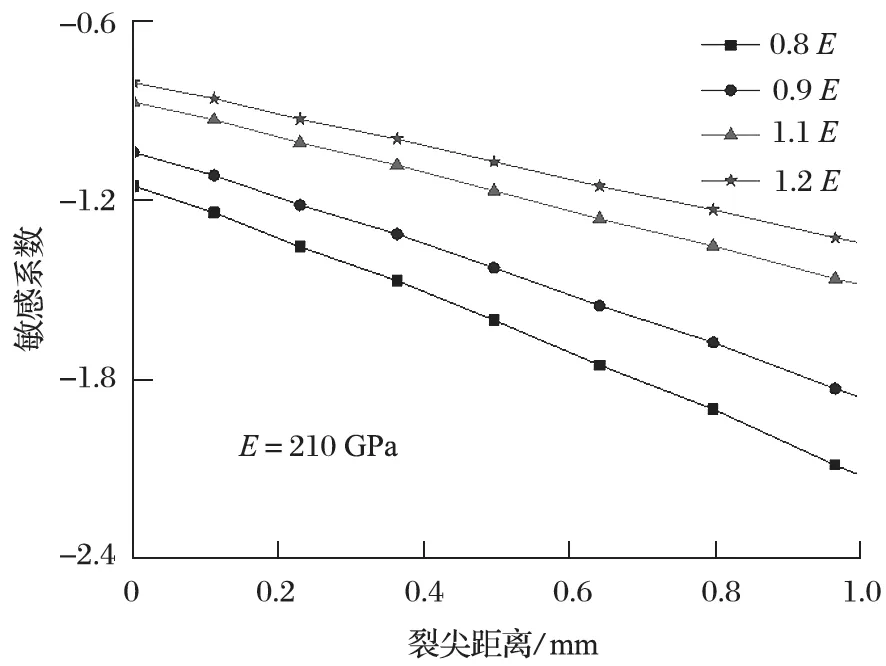
图4 等效塑性应变对弹性模量的敏感性Fig.4 Sensitivity of equivalent plastic strain to elastic modulus

2.3 对硬化指数的敏感性

Mises 应力对材料硬化指数的敏感性如图 5 所示。由图 5 可以看出，敏感系数为负数，裂尖 Mises应力和材料的硬化指数负相关，当材料硬化指数增大时，敏感系数的绝对值减小，敏感性也减小；随着裂尖距离的增大，敏感系数的绝对值也逐渐减小，说明Mises 应力对材料硬化指数的敏感性随着裂尖距离的增大而减小。

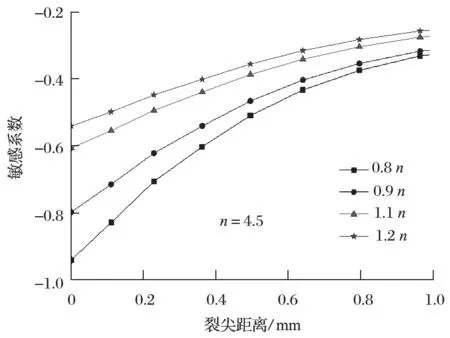
图5 Mises 应力对硬化指数的敏感性Fig.5 Sensitivity of Mises stress to hardening index

裂尖等效塑性应变对材料硬化指数的敏感性如图6 所示。由图 6 可以看出，敏感系数随着裂尖距离的增大先增大后减小，当r＜0.1 mm 时，敏感系数随着硬化指数的增大而增大，且随着r的增大而增大；当0.1 mm ≤r＜0.5 mm 时，敏感系数随着硬化指数的增大而减小，且随着r的增大而增大；当 0.5 mm ≤r＜1 mm 时，敏感系数随着硬化指数的增大而减小，且随着r的增大而减小。敏感系数的最大值出现在离裂尖0.5 mm 处。

图6 等效塑性应变对硬化指数的敏感性Fig.6 Sensitivity of equivalent plastic strain to hardening index

2.4 对泊松比的影响

裂尖 Mises 应力对低碳合金钢泊松比的敏感性如图 7 所示。由图 7 可以看出，敏感系数为负值，Mises 应力和材料的泊松比负相关。从敏感系数的绝对值看，材料的泊松比越大，敏感系数越大，Mises应力对泊松比越敏感；裂尖距离的变化对敏感系数影响不大，材料的泊松比对裂尖 Mises 应力的影响非常小。

图7 Mises 应力对泊松比的敏感性Fig.7 Sensitivity of Mises stress to Poisson's ratio

裂尖等效塑性应变对泊松比的敏感性如图 8 所示。由图 8 可以看出，敏感系数为负值，等效塑性应变和材料的泊松比负相关。从敏感系数的绝对值看，等效塑性应变随着材料泊松比的增大变得越敏感；裂尖距离的变化对敏感系数影响不大。敏感系数远远小于 1，说明等效塑性应变的变化幅值远远小于材料泊松比的变化幅度。

图8 等效塑性应变对泊松比的敏感性Fig.8 Sensitivity of equivalent plastic strain to Poisson's ratio

2.5 裂尖应力应变对偏移系数的敏感性

图9 Mises 应力对偏移系数的敏感性Fig.9 Sensitivity of Mises stress to offset coefficient

裂尖 Mises 应力对材料偏移系数的敏感性如图 9所示。由图 9 可以看出，敏感系数为负值，说明裂尖Mises 应力和材料的偏移系数负相关。从敏感系数的绝对值来看，当r≤0.9 mm 时，材料偏移系数越大，敏感性越小；当r＞0.9 mm 时，材料偏移系数越大，敏感性越大。随着裂尖距离的增大，Mises 应力对偏移系数的敏感性降低。Mises 应力对材料的偏移系数不敏感，也就是材料的偏移系数变化幅度较大时，裂尖 Mises 应力的变化幅度非常小。

等效塑性应变对材料偏移系数的敏感性如图 10所示。由图 10 可以看出，材料的偏移系数越大，敏感系数越小；离裂尖越远，敏感系数越大。敏感系数的最大值小于 1，说明等效塑性应变对材料偏移系数的敏感性较小，等效塑性应变的变化幅值小于材料偏移系数的变化幅值。

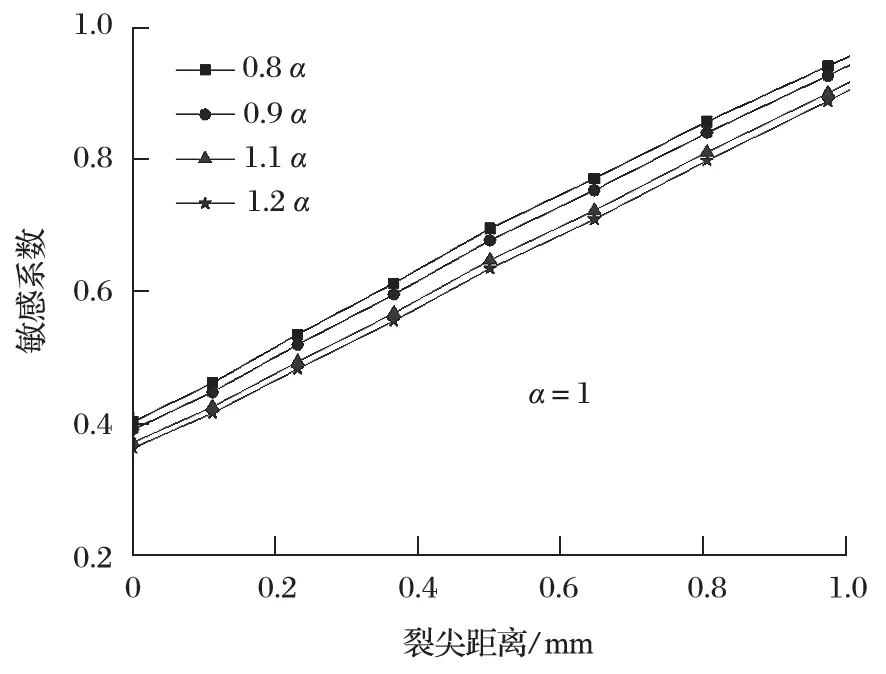
图10 等效塑性应变对偏移系数的敏感性Fig.10 Sensitivity of equivalent plastic strain to offset coefficient

3 结论

(1) 裂纹尖端 Mises 应力对材料各力学参量的敏感性不同。在裂尖最近处，Mises 应力对材料的硬化指数最为敏感，对材料的泊松比最不敏感。按照裂尖最近处 Mises 应力对材料各力学参量敏感性，由高到低排列为：硬化指数、屈服强度、偏移系数、弹性模量和泊松比。

(2) 裂尖等效塑性应变对材料各力学参量的敏感性不同。裂尖最近处等效塑性应变对材料的屈服强度最敏感，对材料的泊松比最不敏感。按照裂尖最近处等效塑性应变对材料力学参量敏感性，由高到低排列为：屈服强度、弹性模量、偏移系数、硬化指数和泊松比。