三节臂轮式液压挖掘机整机理论挖掘力分析

太原科技大学机械工程学院 山西太原 030024

挖 掘机的挖掘力是其作业性能的主要参数之一，也是生产厂商和用户最为关注的性能指标。整机理论挖掘力是进行结构设计和强度计算的依据[1]116，其限制因素包括主动液压缸的发挥能力、被动液压缸的闭锁能力、整机的前后倾稳定性、整机与地面的附着条件、各构件的重力及工作装置的位姿等。三节臂轮式液压挖掘机比两节臂式增加了一个动臂辅助液压缸，该液压缸扩大了挖掘机的作业范围、并增加了其作业灵活性，但对整机挖掘力的发挥存在一定的影响。为了更好地掌握该类型挖掘机挖掘力的发挥情况，为结构设计、性能研究和使用提供借鉴，笔者在参考了相关文献的基础上，利用空间矢量力学原理建立并推导了包括工作装置几何关系和主要限制因素在内的整机理论挖掘力计算公式，并通过实例进行了分析验证。

针对某三节臂轮式液压挖掘机的结构特点，首先对整机理论挖掘力进行理论分析；其次，借助于 Pro/E 建立该机型的虚拟样机模型，然后利用ADAMS 对该机型在铲斗挖掘工况下进行挖掘过程仿真，得出工作装置在固定位姿下的整机理论挖掘力；然后，通过调节动臂辅助液压缸的长度，分析该液压缸在极限长度时对整机理论挖掘力的影响。

1 整机理论挖掘力数学模型

图1 所示为三节臂轮式液压挖掘机的受力分析。其中A、B、C、D、E、F、G、H、K、M、N、Q、U为各铰接点中心，V为铲斗齿尖，G1～G12依次为底盘、转台、下动臂液压缸、下动臂、动臂辅助液压缸、上动臂、斗杆液压缸、斗杆、铲斗液压缸、摇臂、连杆、铲斗的重力，G13为物料的重力，I、J分别为轮胎前、后接地点，r为前后点连线的矢量，Fw为切向挖掘力，其方向为主动液压缸所决定的斗齿运动的切线方向的反向。

根据图 1 用理论力学的方法来推导三节臂轮式液压挖掘机整机理论挖掘力的计算公式。限于篇幅，本文只涉及铲斗主动挖掘，下动臂、上动臂、斗杆液压缸闭锁的工况。铲斗挖掘时，铲斗内物料的重力不断增大，铲斗液压缸长度的线性函数[2]可表示为

式中：Gw为铲斗额定装载物料的重力；L5为铲斗挖掘过程中铲斗液压缸的实时长度；L4为铲斗液压缸的最大长度。

三节臂轮式液压挖掘机整机理论挖掘力的限制因素有下动臂液压缸闭锁、动臂辅助液压缸闭锁、斗杆液压缸闭锁、铲斗液压缸主动发挥、前倾稳定性、后倾稳定性以及地面附着力。针对这 7 个限制因素对整机理论挖掘力进行分析[1]119-120。

(1) 下动臂液压缸闭锁限制的整机理论挖掘力

当下动臂液压缸受压时，

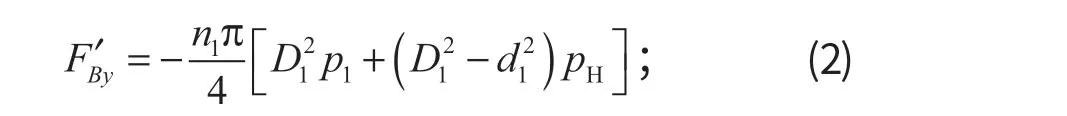
当下动臂液压缸受拉时，

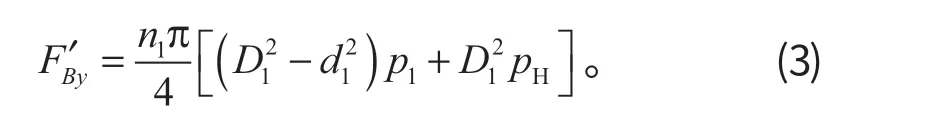
式中：n1为下动臂液压缸数量；D1为下动臂液压缸缸径；d1为下动臂液压缸活塞杆直径；p1为下动臂液压缸闭锁压力；pH为下动臂液压缸回油压力。

隔离下动臂液压缸进行受力分析，对A点取矩得

式中：γ为下动臂液压缸与水平面的夹角。

推导后得

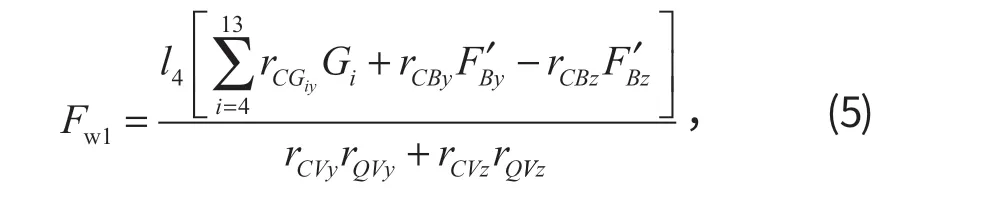
式中：l4为铲斗的长度，l4=|rQV|；rCGiy为C点指向工作装置各部件重心位置的矢量在y方向的分量；Gi为各部件的重力，i=4，5，…，13。

(2) 动臂辅助液压缸闭锁限制的整机理论挖掘力

当动臂辅助液压缸受压时，

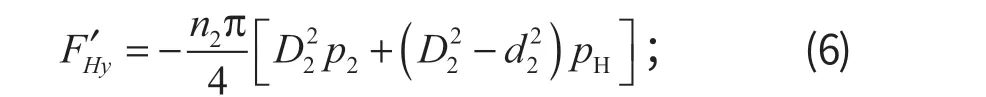
当动臂辅助液压缸受拉时，

式中：n2为动臂辅助液压缸数量；D2为动臂辅助液压缸缸径；d2为动臂辅助液压缸活塞杆直径；p2为动臂辅助液压缸闭锁压力；pH为动臂辅助液压缸回油压力。

隔离动臂辅助液压缸进行受力分析，对U点取矩得

图1 三节臂轮式液压挖掘机整机受力分析Fig.1 Force analysis of three-arm wheeled hydraulic excavator

式中：β为动臂辅助液压缸与水平面的夹角。

推导后得

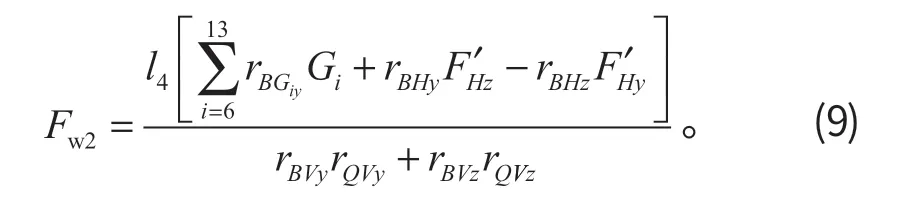
(3) 斗杆液压缸闭锁限制的整机理论挖掘力

当斗杆液压缸受压时，

当斗杆液压缸受拉时，

式中：n3为斗杆液压缸数量；D3为斗杆液压缸缸径；d3为斗杆液压缸活塞杆直径；p3为斗杆液压缸闭锁压力；pH为斗杆液压缸回油压力。

隔离斗杆液压缸进行受力分析，对D点取矩得

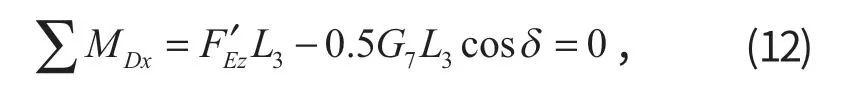
式中：δ为斗杆液压缸与水平面的夹角。

推导后得

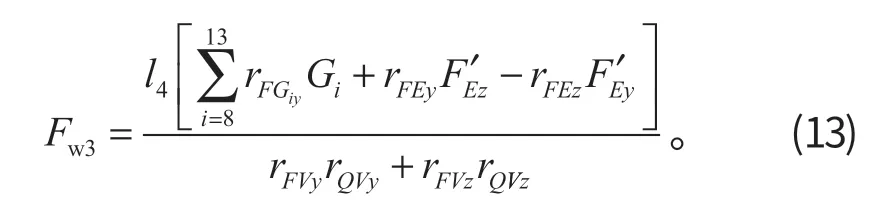
(4) 铲斗液压缸大腔主动发挥限制的整机理论挖掘力

当铲斗液压缸伸长时，

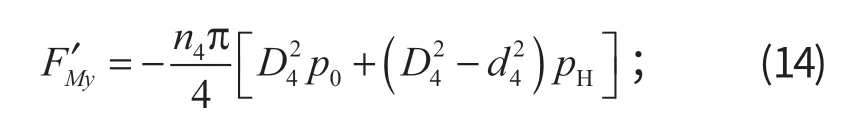
当铲斗液压缸缩短时，

隔离铲斗液压缸进行受力分析，对G点取矩得

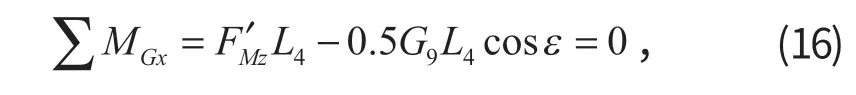
式中：ε为铲斗液压缸与水平面的夹角。

隔离连杆对M点取矩，再隔离摇臂连杆对N点列力矩平衡方程，求得FKy和FKz，可得

(5) 前倾稳定性限制的整机理论挖掘力

前倾稳定性限制下，

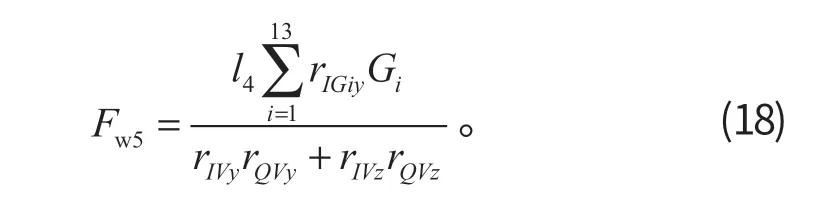
当Fw5>0 时，存在前倾失稳问题；当Fw5<0 时，不会发生前倾失稳。

(6) 后倾稳定性限制的整机理论挖掘力

后倾稳定性限制下，

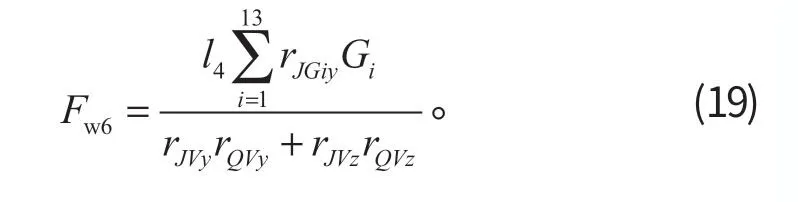
当Fw6>0 时，存在后倾失稳问题；当Fw6<0 时，不会发生后倾失稳。

(7) 地面附着力限制的整机理论挖掘力

地面附着力限制下，

当Fw7y＞0 时，存在向前滑移的趋势，

当Fw7y＜0 时，存在向后滑移的趋势，

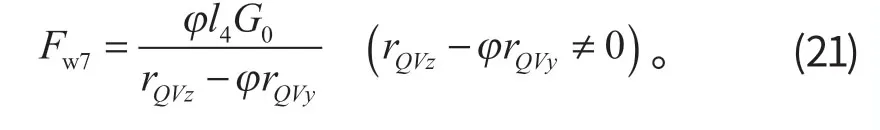
式中：φ为附着系数；G0为整机重力。

当Fw=∞时，不会产生滑移。

综上所述，整机最大理论挖掘力取决于Fw1～Fw7中的最小值[1]120-131，即

上述为铲斗液压缸挖掘、其他液压缸闭锁时整机理论挖掘力的计算公式。对于斗杆挖掘工况，其计算过程类似，区别在于斗杆液压缸作业时，整机理论挖掘力的方向为齿尖绕F点转动的切线方向，阻力臂为rFV[3]。

2 ADAMS 虚拟样机模型

根据样本数据，在 Pro/E 中搭建三节臂轮式液压挖掘机的三维模型。为了便于仿真，对回转平台和底盘进行了适当简化。将该模型保存为 .Parasolid 格式导入 ADAMS 中[4]。在 ADAMS 中，原有的约束已经失效，需重新添加约束。首先用布尔和运算将三节臂轮式液压挖掘机工作装置的各个子零件组装成一个整体，材料定义为刚体，并添加约束。然后将各个部件组装在一起，底盘与地面固定，回转平台和底盘之间添加旋转副，各铰接点之间添加旋转副、圆柱副、点线副和球副，在工作液压缸与活塞杆之间添加移动副。最后将长度单位统一设置为 mm，力单位设置为 N，重力方向竖直向下，重力加速度的大小为9 806.65 mm/s2[5]。验证模型，该模型的自由度为 5，模型验证正确。由此建立 ADAMS 的虚拟样机模型如图 2 所示。

图2 三节臂轮式液压挖掘机 ADAMS 虚拟样机模型Fig.2 ADAMS virtual prototype model of three-arm wheeled hydraulic excavator

3 整机理论挖掘力仿真

选取停机面上的最大挖掘半径工况，该工况下，铲斗挖掘，轮胎支地。经计算得出下动臂液压缸大腔的闭锁力为 866.3 kN，小腔的闭锁力为 519.4 kN；动臂辅助液压缸大腔的闭锁力为 899.4 kN，小腔的闭锁力为 625.8 kN；斗杆液压缸大腔的闭锁力为 504.9 kN，小腔的闭锁力为 285.5 kN；铲斗液压缸大腔的闭锁力为 334.9 kN，铲斗液压缸小腔的闭锁力为 161.4 kN。

在 Pro/E 中将三节臂轮式液压挖掘机调节为最大挖掘半径工况，导入 ADAMS 中依次添加相应的约束。对各限制因素进行分析，将转台及各液压缸的驱动函数设置为 0，在下动臂、上动臂、斗杆上依次添加闭锁力载荷，在铲斗上添加主动力载荷，在铲斗挖掘轨迹的切线方向创建附着在大地上的 Maker 点，在该点与斗齿尖创建刚度系数较大的弹簧 SPR_1，使弹簧在外力作用下的变形忽略不计。

在轮胎接地的对称平面，即前后倾覆点分别建立旋转副 I 和 J，为分析前倾稳定性和后倾稳定性限制的整机理论挖掘力做准备。

建立测量整机滑移稳定性的约束副，在底盘与大地之间创建平面副 Planar，在铲斗齿尖挖掘轨迹切线方向创建力载荷 force，方向与铲斗运动方向相反。在平面副 Planar 上创建测量 Planar_FY，得到地面对整机的法向力，在力载荷上创建测量，得到该合力的值 force_F、水平分量 force_FX 和垂直分量 force_FY。最后创建传感器 sensor_1，其表达式为 IF (force_FX：-1，0，0.6* (Planar_FY+force_FY) -force_FX)。当该值小于等于零时停止仿真，从而得到地面附着力限制的整机理论挖掘力[6]。设置好的仿真模型如图 3 所示。

图3 三节臂轮式液压挖掘机仿真模型Fig.3 Simulation model of three-arm wheeled hydraulic excavator

对停机面上最大挖掘半径工况下限制整机理论挖掘力的影响因素分别设置如下。

(1) 分析下动臂液压缸限制因素时，失效旋转副I、J、Planar、force、动臂辅助液压缸闭锁力、斗杆液压缸闭锁力、铲斗液压缸主动力、驱动 motion1 和传感器，激活下动臂液压缸的力载荷，设置时间，进行仿真，测量弹簧力的值。同理，在对动臂辅助、斗杆、铲斗液压缸的限制因素进行仿真时，激活相应的力载荷，失效相应的驱动，即可得到铲斗齿尖弹簧力的变化。

(2) 计算前倾稳定性限制的整机理论挖掘力时，失效固定副及液压缸的力载荷，激活液压缸的驱动和旋转副 I，仿真得出弹簧力的变化。同理，在计算后倾稳定性限制的整机理论挖掘力时，只需激活旋转副J，失效旋转副 I 即可。

(3) 计算地面附着力限制的整机理论挖掘力时，失效旋转副 J 及弹簧力，激活平面副 Planar、载荷force 及传感器 sensor_1。

停机面上最大挖掘半径工况仿真结果如图 4 所示。由图 4 可以看出，该工况下挖掘机不会发生前倾失稳。整机理论挖掘力的限制因素为后倾稳定性，此时挖掘机的整机理论挖掘力为 34.9 kN，证明轮胎支地时该挖掘机具有一定的自救能力。在支腿和推土铲放下时，限制整机理论挖掘力的潜在因素为动臂辅助液压缸的闭锁能力。

图4 停机面上最大挖掘半径工况仿真结果Fig.4 Simulation results in operation mode of maximum excavation radius on shutdown surface

为了研究铲斗挖掘时动臂辅助液压缸对整机理论挖掘力的影响，选取除动臂辅助液压缸外各液压缸作用力臂最大的工况进行研究。在 Pro/E 中对各液压缸长度进行调节，测量得出下动臂液压缸的长度为 1 428 mm，斗杆液压缸的长度为 2 383 mm，铲斗液压缸的长度为 2 030 mm。动臂辅助液压缸行程为500 mm，将动臂辅助液压缸的长度从小到大选取 6个数值，最短为 1 114 mm，最长为 1 614 mm，导入ADAMS 中进行整机理论挖掘力的分析计算[7]。

动臂辅助液压缸处于最短和最长时的整机理论挖掘力仿真结果分别如图 5、6 所示。

图5 动臂辅助液压缸最短时的整机理论挖掘力仿真Fig.5 Simulation of theoretical excavation force of whole excavator while boom auxiliary cylinder being shortest

动臂辅助液压缸不同长度时各因素限制下的最大整机理论挖掘力如表 1 所列，其中工况 1～ 6 为动臂辅助液压缸长度由最短到最长。由表 1 可以看出，铲斗挖掘时，随着动臂辅助液压缸长度不断增大，铲斗液压缸大腔主动发挥限制的整机理论挖掘力不断增加。当动臂辅助液压缸长度为 1 614 mm 时，动臂辅助液压缸成为整机理论挖掘力的限制因素，此时整机理论挖掘力为 102.7 kN。当动臂辅助液压缸的长度为1 114 mm 时，最大整机理论挖掘力为 118.7 kN，限制因素为斗杆液压缸的闭锁力，与样本值 126.0 kN 相比存在 5.79% 的误差。这是由于在原始数据中可能存在部件重力和重心位置与样本机型存在差异、仿真数据点不足等原因。此外，最大整机理论挖掘力发挥的位置并不是动臂液压缸和斗杆液压缸作用力臂最大的位置，其受多种因素的影响，而不仅仅是几何因素决定的[3]。

表1 动臂辅助液压缸不同长度时各因素限制下的最大整机理论挖掘力Tab.1 Maximum theoretical excavation force of whole excavator at various length of boom auxiliary cylinder under limit of various factors kN

4 结论

(1) 针对三节臂轮式液压挖掘机，推导出 7 个主要限制因素下的整机理论挖掘力计算公式。用 Pro/E和 ADAMS 软件建立虚拟样机模型，并对典型工况进行仿真，为分析整机理论挖掘力提供了一种新的方法。

(2) 由仿真结果可知，在停机面最大挖掘半径工况且轮胎支地时，后倾稳定性限制了整机理论挖掘力的发挥，证明该挖掘机具有一定的自救能力。

(3) 当下动臂液压缸力臂最大、斗杆液压缸力臂最大、动臂辅助液压缸最短且铲斗转至铲斗连杆传动比最大位置时，三节臂轮式液压挖掘机的整机理论挖掘力达到最大。

(4) 当动臂辅助液压缸最长时，其闭锁能力最薄弱，限制了整机挖掘力的发挥。