一类新型的Bernstein算子的逼近性质

傅仙发

(湄洲湾职业技术学院 基础部，福建 莆田 351254)

0 引言

最近，文[1]引入了一类新型的Bernstein算子

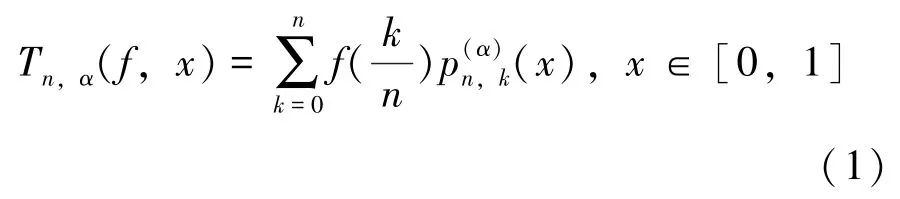
其中，

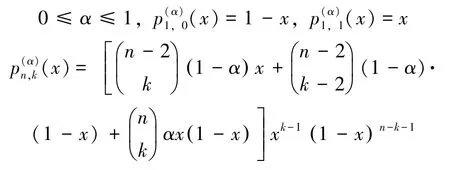
在文[1]中，作者研究了算子Tn，α的某些逼近性质，其中包括一致收敛、算子保形及Voronovskaya型渐近展开等。此后，跟该算子相关的研究工作成为一个热点，见文[2-3]。

Bojanic等开创了算子对导数为有界变差的连续函数的研究工作[4]，接着曾晓明等在这方面做了深入的推广[5-7]。

本文在文[1]研究的基础上，利用Ditzian-Totik光滑模，研究了算子Tn，α的收敛性质，再根据经典的Bojanic-Cheng分解方法，结合分析技术，讨论了该算子对一类导数为有界变差的函数类的逼近。

首先给出一些基本的定义。令：

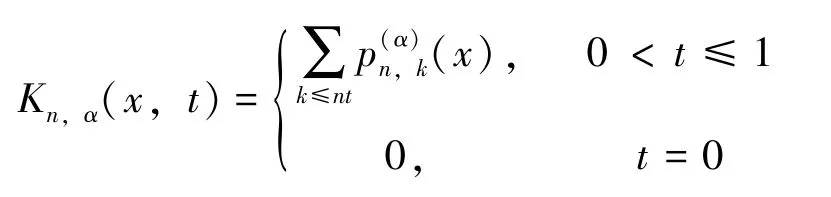
则由Lebesgue-Stieltjes积分形式，算子Tn，α可以表示为：

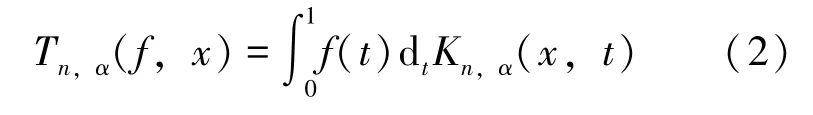
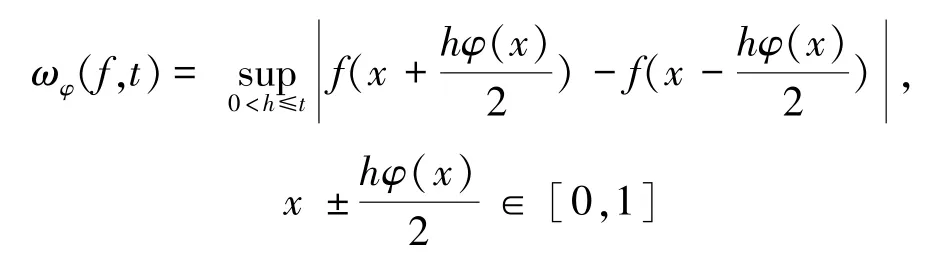
相应的K泛函定义为：

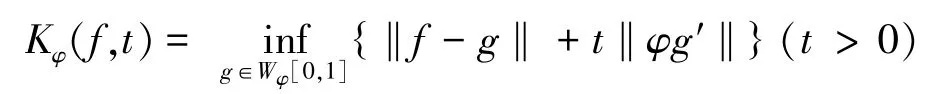
其中Wφ(0，1)={g：g∈AC[0，1]，‖φg′‖＜∞}，而AC[0，1]是区间[0，1]上的绝对连续函数。

设BV[0，1]表示区间[0，1]上的有界变差函数。定义

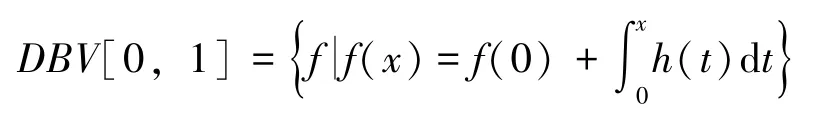
其中x∈[0，1]，h∈BV[0，1]。

1 引理

引理1[1]设x∈[0，1]则有：

注1 经过简单的计算，有：

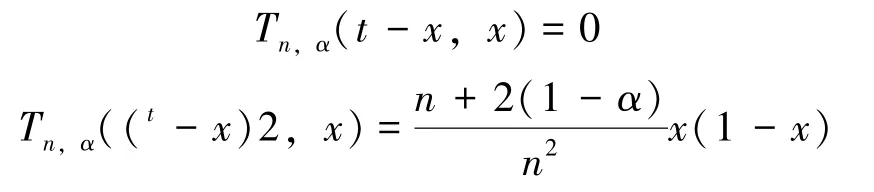
注2 由Cauchy-Schwarz不等式及注1，得

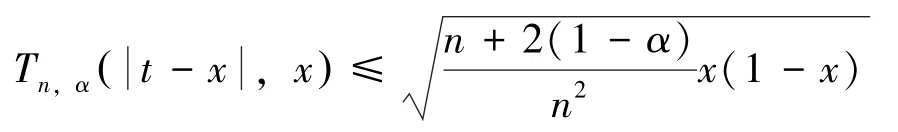
引理2 设f∈C[0，1]，则有：

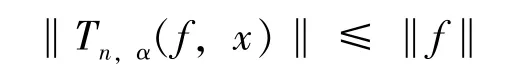
证 由算子Tn，α的定义及引理1，可得

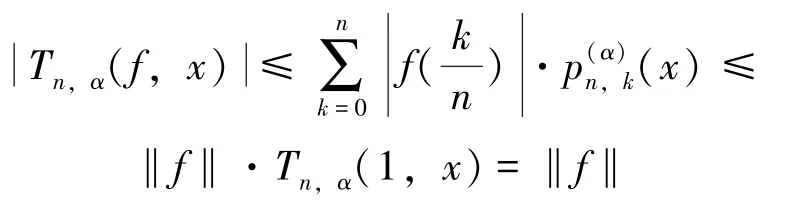
引理3 设0≤y＜x＜1，当n足够大时，有：

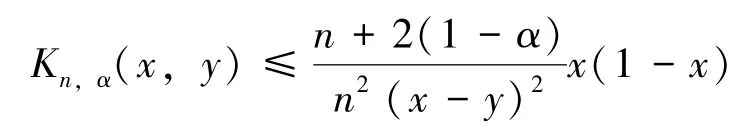
证 由式(2)和注1，得：

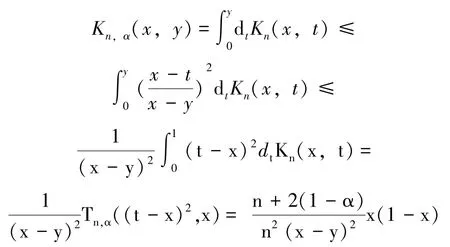
引理4[8]设f(x)∈C[0，1]，则存在常数C＞0，使得：

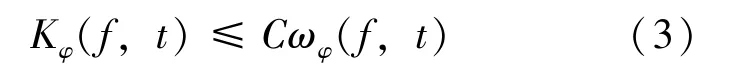
2 定理及证明

定理1 设f(x)∈C[0，1]，x∈[0，1]，则存在常数C＞0，使得：

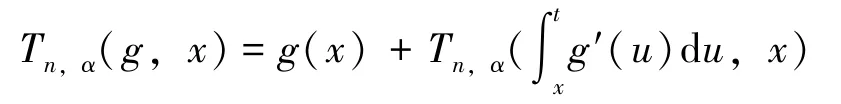
对任意的x，t∈(0，1)，有：

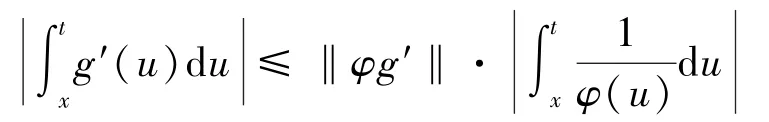
且

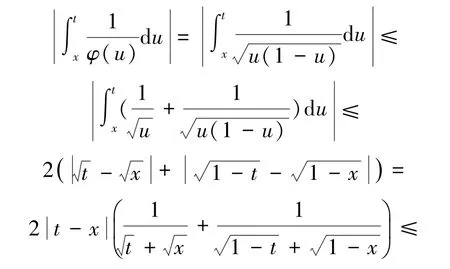
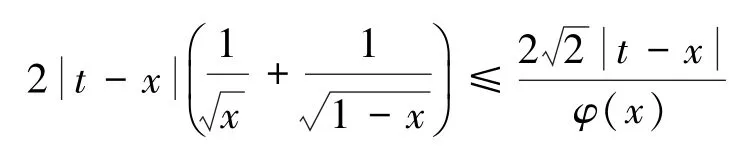
由Cauchy-Schwarz不等式及注2，得：

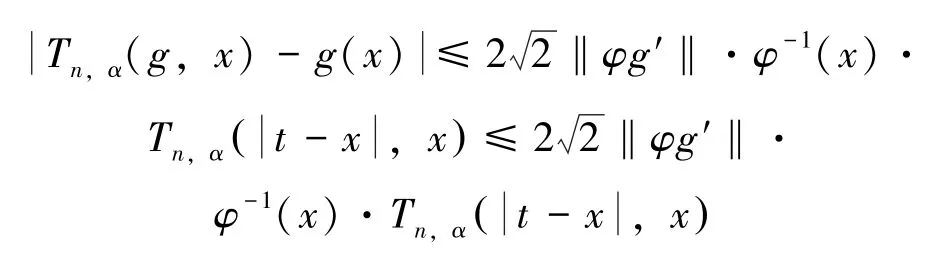
因此，有：

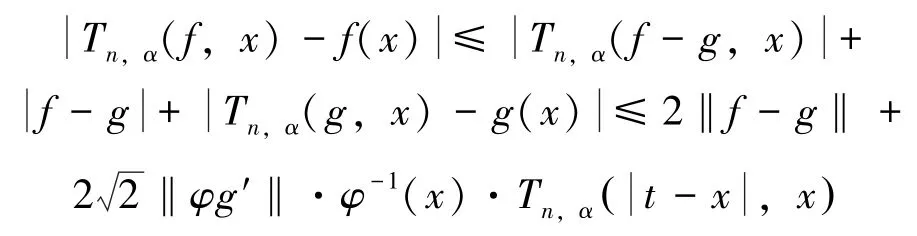
对所有的g∈Wφ(0，1)，上式取下确界，得：

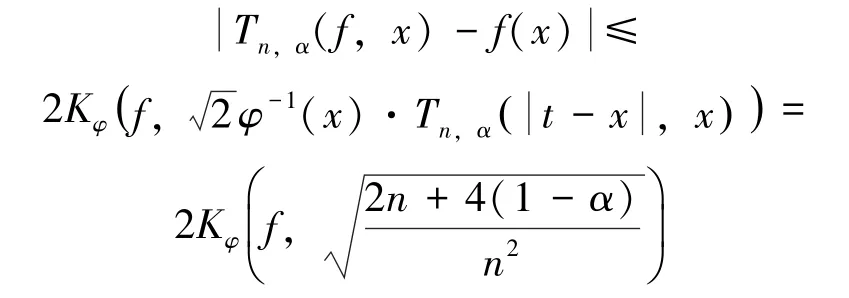
最后一个等式由注2得到。根据引理4可知定理1成立。

定理2 设f∈DBV[0，1]，对任意的x∈(0，1)，h(x＋)，h(x-)存在，有：

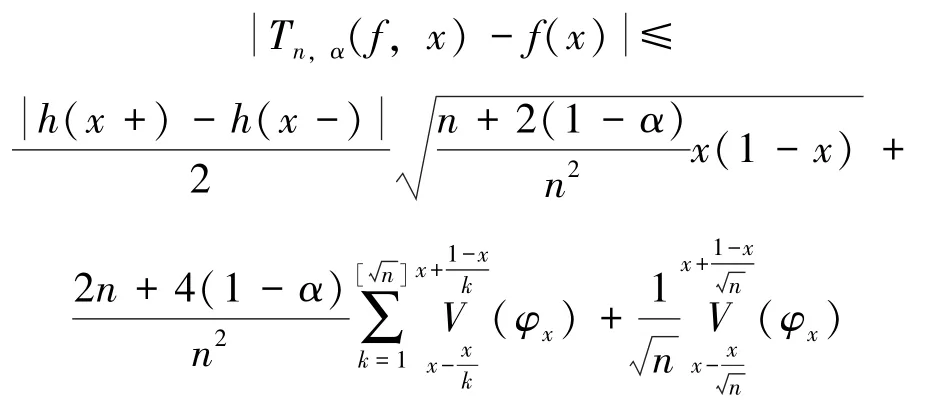
其中

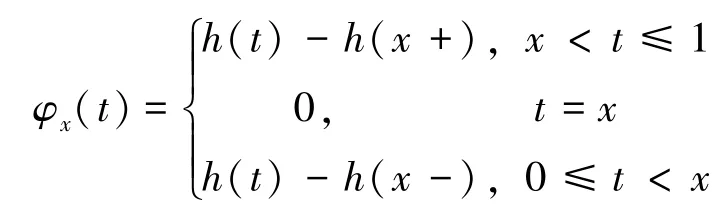
证 由定理2的条件，得：

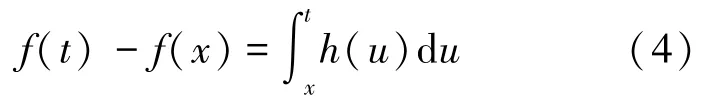
而根据Bojanic-Cheng分解，有：

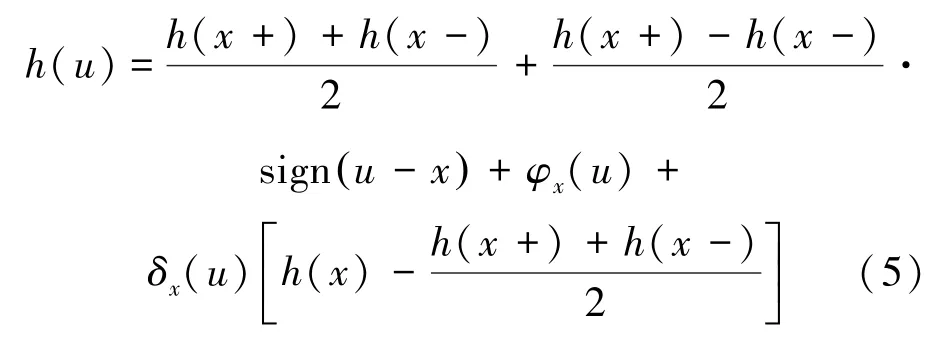
其中φx(u)如前面定理的条件所定义，并且

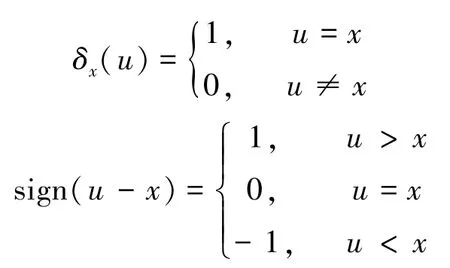
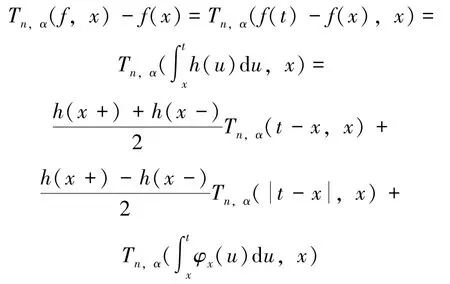
由注1，得：

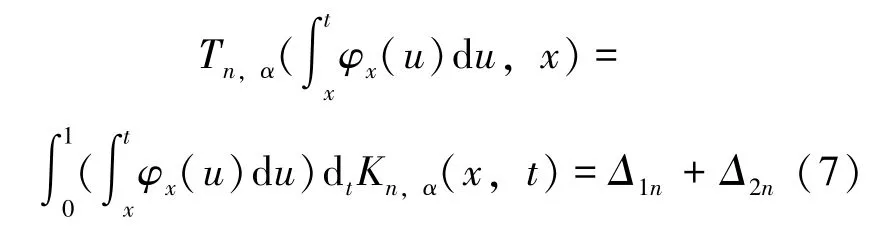
其中

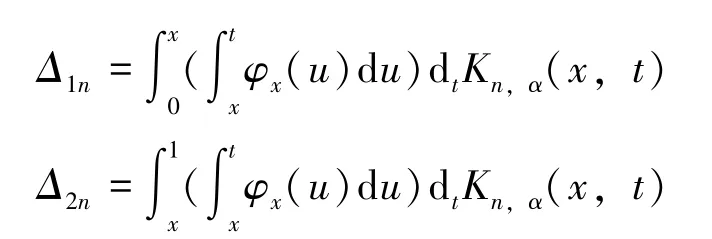
首先计算Δ1n，运用分部积分法，得：

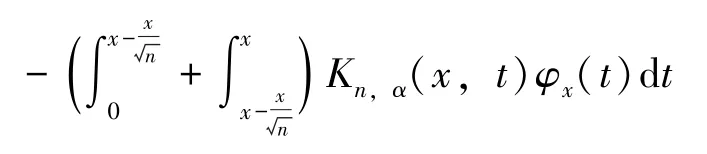
所以

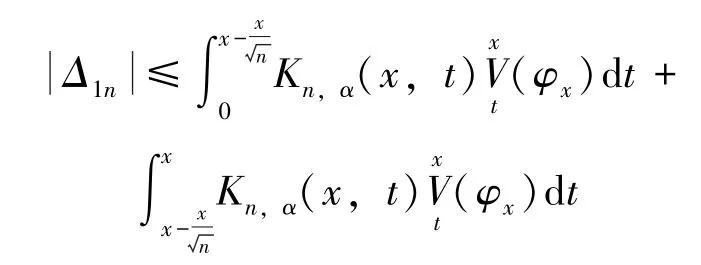
由引理3及0≤Kn，α(x，t)≤1，得：

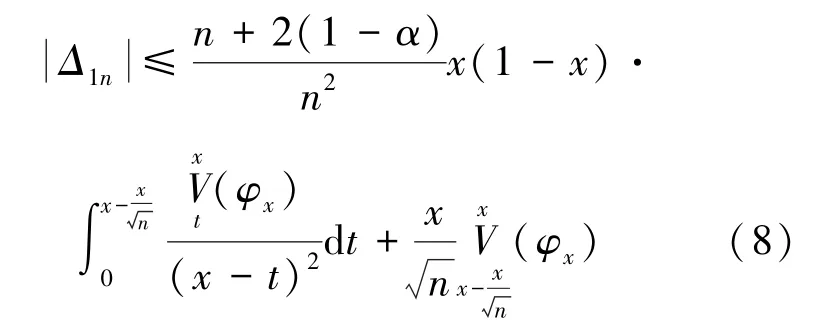
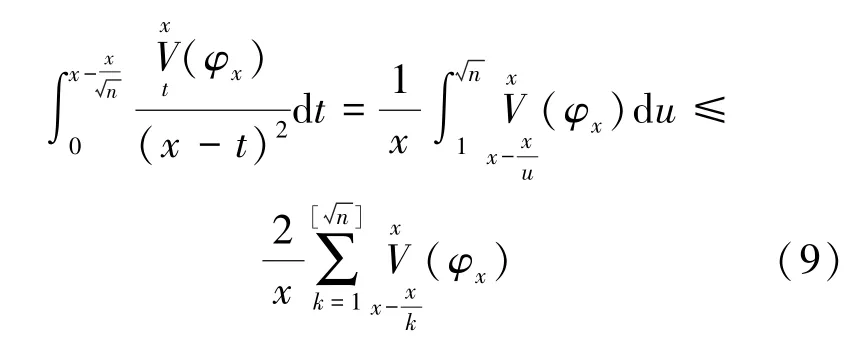
由式(8)和(9)，得：

类似的估计，可以得到：

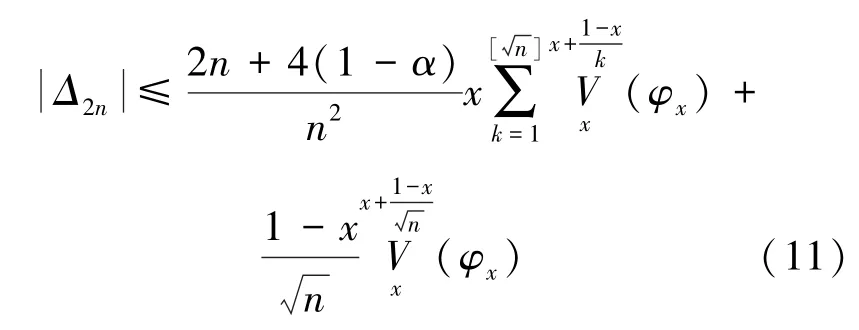
由式(6)～(11)及注2即得定理2。