半封闭捕获对具恐惧效应的捕食系统的影响

石志高

(福建江夏学院 数理教研部，福建 福州 350108)

0 引言

随着经济和科技的不断发展，人类对自然资源的开发更为迫切。对自然资源的过度开发，如捕食野生动物、过度砍伐树木、过度破坏植被等，必然导致生态系统失去平衡，某些物种濒临灭绝。因此，为了维持生态系统的持久稳定，可以通过建立半封闭或全封闭禁猎区、人工植树等方式保护生态系统。众多学者对生态系统中的食饵-捕食者系统进行了大量研究，特别是Holling功能反应和Beddington-DeAngelis功能反应模型[1-4]，取得了丰富的成果，但对具有半封闭区域捕获的研究还不多。文[4]研究了具有半封闭区域的Beddington-DeAngelis捕食系统：

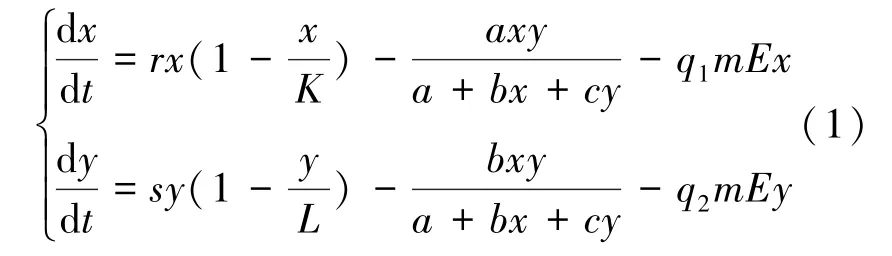
其中：x，y分别表示食饵和捕食者种群的时间密度函数，t表示时间，r，s分别表示食饵和捕食者种群的内禀增长率，K，L分别表示食饵在没有捕食者的情况下和捕食者缺乏食饵的情况下的生存能力，捕食者以Beddington-DeAngelis功能反应函数来消费食饵，而以来供给自身生长率，q1，q2分别是两种群的捕捞系数，m(0＜m＜1)表示半封闭区域可供捕获的比例，E是捕捞努力量。文[4]对系统(1)的正平衡点的全局稳定性进行研究。文[5]考虑捕获对半封闭捕获Lotka-Volterra系统：

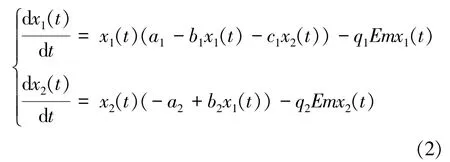
讨论了m(0＜m＜1)对系统动力学行为的影响，其中m表示整块区域中可供捕获的比例。另外，食饵由于被捕食而产生的恐惧效应，在一定程度上会影响其繁殖能力，使种群数量增长较慢。一般用来刻画恐惧对捕食率造成的影响，m(m≥0)表示食饵种群受到恐惧的程度，y表示捕食者种群的时间密度函数。文[6]研究恐惧效应为常数的系统：

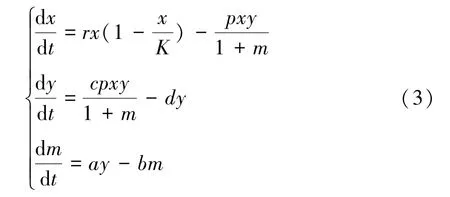
讨论了正平衡点的全局稳定性。受上述启发，本文考虑系统：

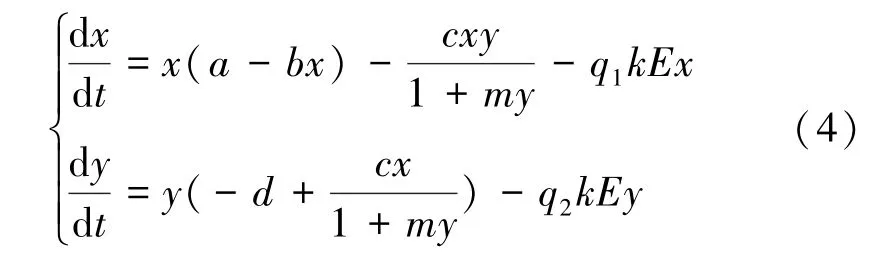
其中：a，b，c，d，q1，q2，k，m均为正常数，a-bx表示食饵种群的内部增长率，c表示两种群的相互作用系数，d表示捕食者的死亡率，0＜k＜1表示整块区域中可供捕获的比例，m(m≥0)表示食饵种群受到恐惧的程度，表示恐惧对捕食率造成的影响，E是捕捞努力量，q1，q2分别为食饵和捕食者的捕捞系数，由系统的生态意义，仅在对系统(4)进行讨论。

1 主要结果

对系统(4)作无量纲时间变换dτ=

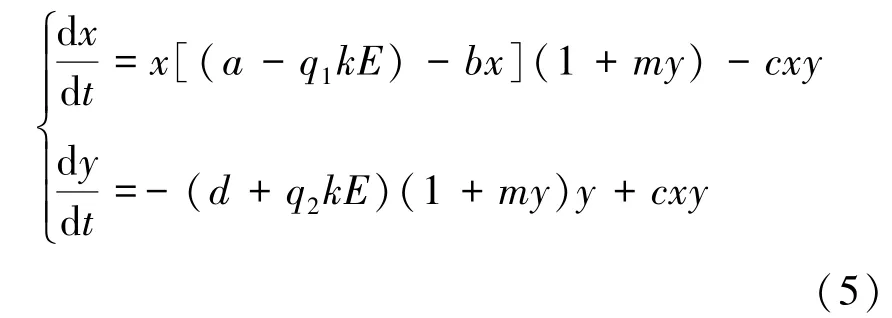
通过计算易得系统(5)存在平衡点的情形，具体如下：

1)0＜a＜q1kE时，系统(5)只有平衡点O(0，0)；

3)当a=q1kE时，边界平衡点A(x1，0)重合于O(0，0)；

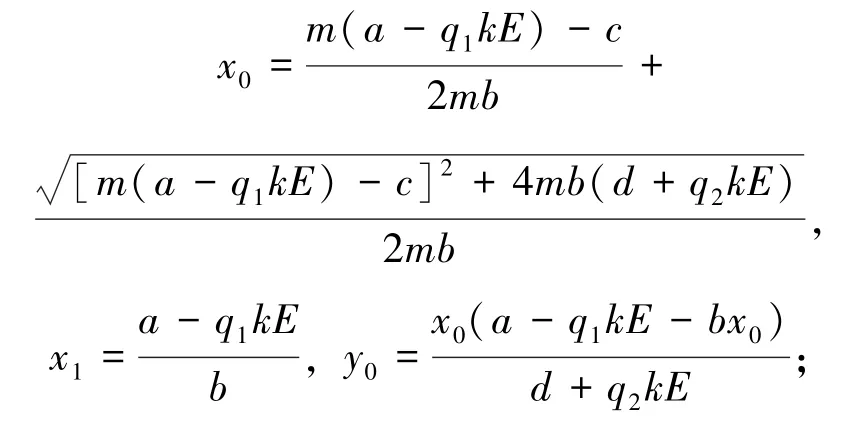
定理1 1)当0＜a＜q1kE时，平衡点O(0，0)是稳定的结点；

2)当q1kE＜a＜q1kE＋时，平衡点O(0，0)是鞍点，边界平衡点A(x1，0)是稳定的结点；

3)当a＞q1kE＋时，平衡点O(0，0)和边界平衡点A(x1，0)都是鞍点，正平衡点B(x0，y0)是稳定的结点。

证 系统(5)的雅克比矩阵为

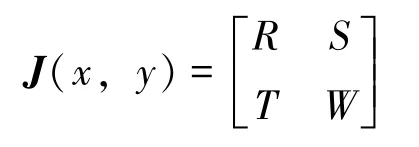
其中：R=(a-q1kE-2bx)(1＋my)-cy，S=mx(a-q1kE-bx)-cx，T=cy，W=-(d＋q2kE)(1＋my)-(d＋q2kE)my＋cx。

则有

1)当0＜a＜q1kE时，

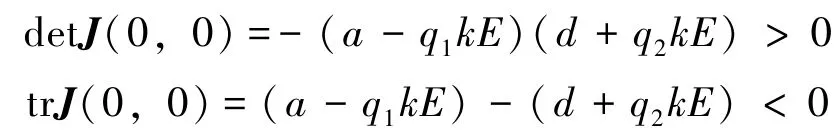
此时，O(0，0)是稳定的结点。

2)当q1kE＜a＜q1kE＋时，

det J(0，0)=-(a-q1kE)(d＋q2kE)＜0此时，O(0，0)是鞍点。

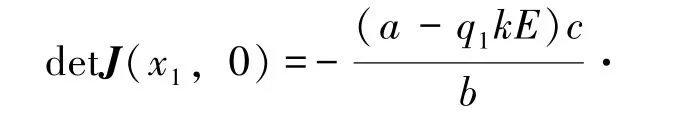
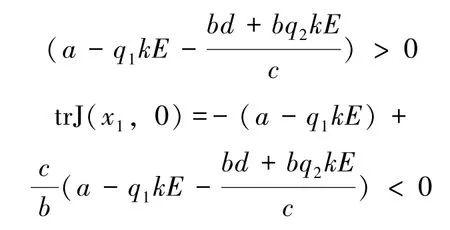
故A(x1，0)是稳定的结点。

3)当a＞q1kE＋时，

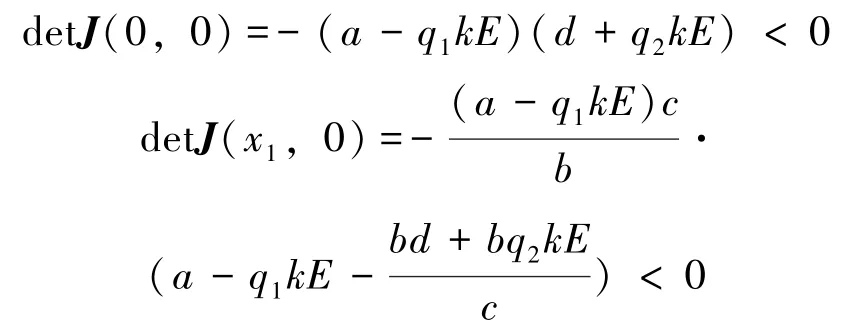
故O(0，0)和A(x1，0)都是鞍点。

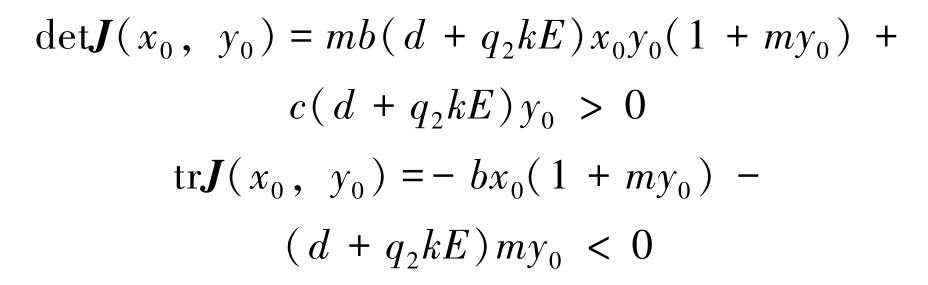
故B(x0，y0)是稳定的结点。证毕。

由上述结论可以看到，当0＜a＜q1kE时，平衡点O(0，0)是局部稳定的结点，说明对食饵种群的过度捕获且超过种群自身增长率时，将引起食饵种群的灭绝，从而导致捕食者种群也将逐渐灭绝。而当q1kE＜a＜q1kE＋时，边界平衡点A(x1，0)是稳定的结点。说明对食饵种群自身增长超过人为捕获时，食饵种群会相对稳定，但不控制对捕食者种群的捕获区域时，捕食者种群最终将灭绝。当a＞q1kE＋时，正平衡点B(x0，y0)是稳定的结点。说明当食饵种群自身增长远超过人为捕获，且适当控制人为的捕获区域时，两种群将能够长久共存。即无论保护区域外的捕捞的强度多大，只要限制的保护区域的范围足够大，那么两种群都能长久共存。因此，研究正平衡点的全局稳定性具有重要的生态意义。

定理2 当a＞q1kE＋时，正平衡点B(x0，y0)是全局渐近稳定的。

证 由定理1可知，当a ＞q1kE＋时，正平衡点B(x0，y0)是局部渐近稳定的，如果可以证明系统(5)在G=

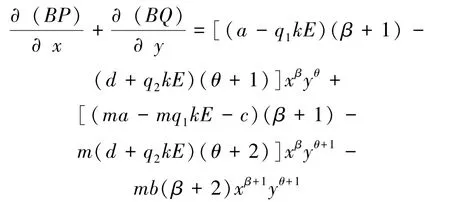
2 数值仿真

例1 取a=3，b=0.25，c=4，d=2，m=3，q1=1，q2=2，k=0.5，E=8。考虑系统：

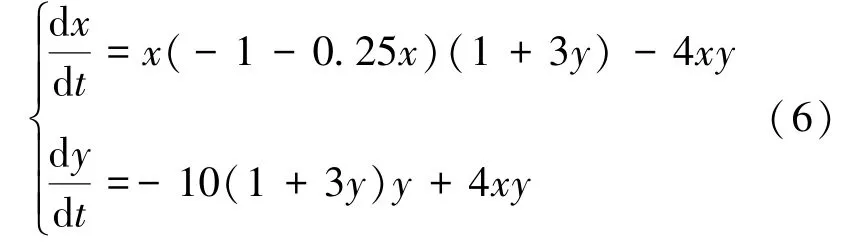
满足a＜q1kE，系统(6)仅有平衡点O(0，0)是稳定的结点。图1是系统(6)在初值为x(0)=5，y(0)=3的解的数值仿真图。从图1可以看出两种群在半封闭区域被过度捕捞(捕捞努力量E=8)，导致两种群最终灭绝。

例2 仅改变捕捞努力量，取E=5.5，其余系数不变。考虑系统：

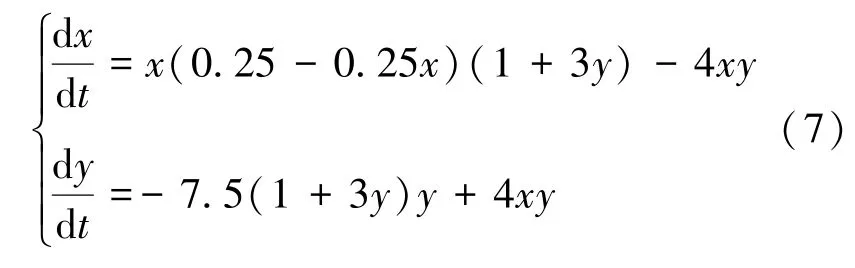
图1 系统(6)的数值仿真图

满足q1kE＜a＜q1kE＋，系统(7)存在是稳定的结点A(1，0)。图2是系统(7)在初值为x(0)=5，y(0)=3的解的数值仿真图。从图2可以看出在半封闭区域过度捕捞捕食者种群(捕捞努力量E=5.5)，使得捕食者种群最终灭绝，而虽然食饵种群也遭到适当强度捕捞，但是由于捕食者种群趋于灭绝，使得食饵种群数量反而增加。

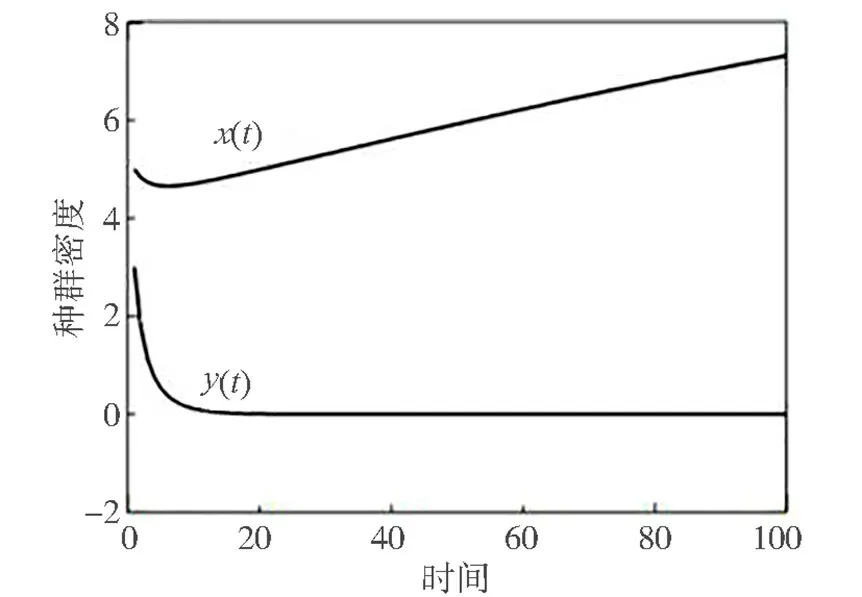
图2 系统(7)的数值仿真图

例3 仅改变捕捞努力量，取E=2，其余系数不变。考虑系统：

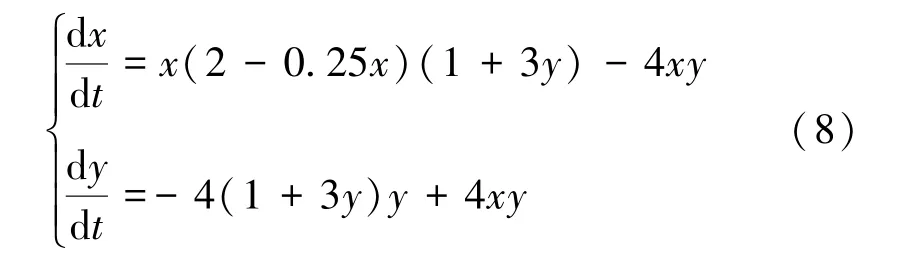
满足a＞q1kE＋，系统(8)存在正平衡点B(4，1)，且是全局渐近稳定的。图3是系统(8)在初值为x(0)=5，y(0)=3的解的数值仿真图。从图3可以看出两种群在半封闭区域适当捕捞(捕捞努力量E=2)，使得两种群能够长久共存。

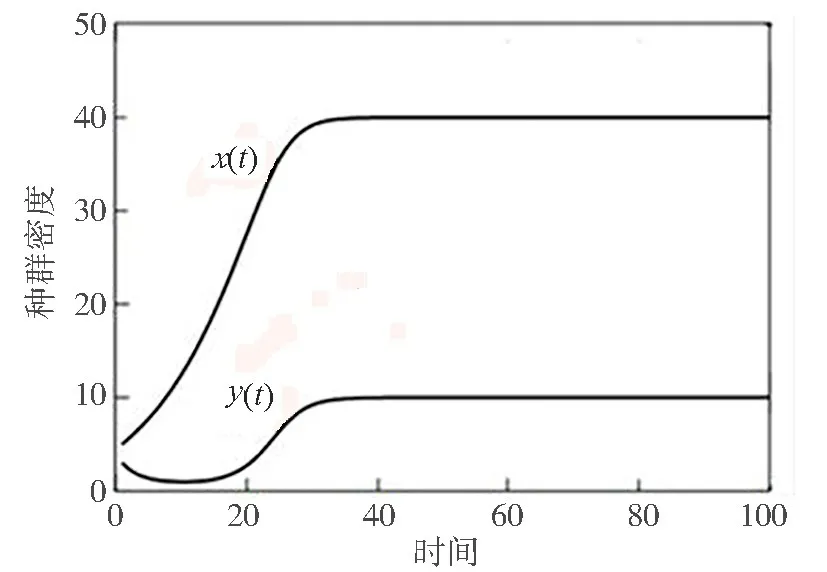
图3 系统(8)的数值仿真图