初中数学方程思维的运用研究

杨繁

摘 要 方程思维在初中数学解题中有着非常重要的作用，本文将主要从方程思维的相关背景、方程思维在教学中目前存在的问题等方面进行阐述，并对方程思维在实际教学中的研究进行总结。

关键词 方程思维;数学思想;教学途径

中图分类号：G632 文献标识码：A 文章编号：1002-7661（2020）06-0111-01

方程思维在初中数学解题有重要作用，但在实际教学中，一些教师对学生方程思维模式的培养还存在一定的问题。对此，笔者进行了探究与总结。

一、方程思维理论的相关背景介绍

（一）方程思维概念介绍。方程思维是一种简化问题的思维方式，也是将问题中已知元素与未知元素用另一种辩证的方法表示出来的形式，它将用汉语描述的名词间的等量关系用数学符号列成方程式表示出来。

（二）方程思维与数学思想的关系。通常在解决一道数学问题时，不仅仅应用到一种数学思想，需要各种数学思想之间相辅相成，共同的目标是帮助学生以更省时、更简便的方式解决问题。比如，在解决下面这道应用题时，就将多种数学思想相结合在一起。

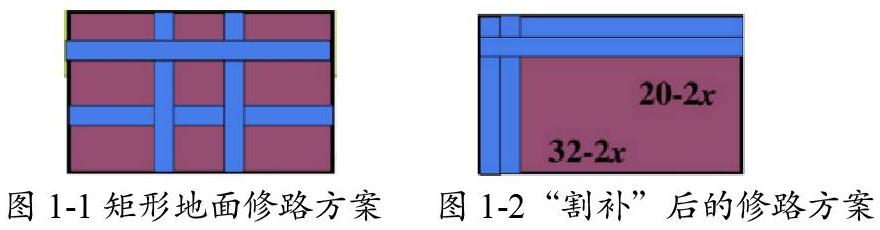
例题：某企业需要在宽为19m，长为35m的空地上铺路，宽度相等，粉色面积需要铺上草坪，若企业需要让草坪面积保持为520m2，请计算出路的宽度。修路方案如下图1-1所示。

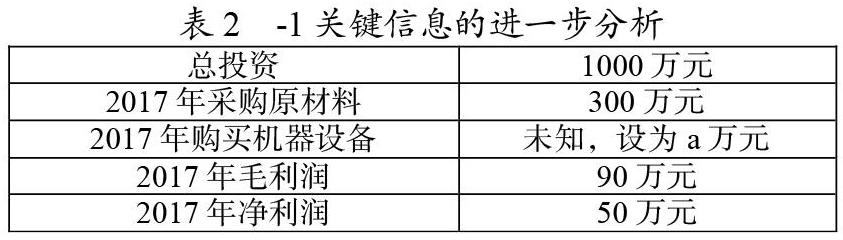
如果学生在拿到题目后没有运用一定的转化思想，直接运用方程思想，将题目中找到的等量关系“草坪面积=520”用数学符号表示出来，则是将图1-1中草坪的面积按照方案中给出的9个部分分别求出再加和。但如果学生同时掌握了转化思维，将图1-1的修路方案通过“割补”后整合为图1-2，设定道路的宽为x米，则草坪部分的面积将非常容易地表示为（19-2x）×（35-2x）。

图1-1矩形地面修路方案 圖1-2“割补”后的修路方案

二、关于方程思维在实际教学中的研究

针对教师在教学过程中初次引入方程思维的例题选取不恰当的问题，教师在教学过程中要注意学生的吸收成效，注重积累课后学生作出的反馈，将学生提出的问题进行整改，同时要旁听优秀教师的讲课，将优秀教师提出的教学例题积累总结，归纳出特点，注重和优秀教师的交流沟通，少走弯路。教师还要创新教学模式，比如笔者经过多年的教学实践，总结出下面这套经验，那就是在教学时教会学生将题目中的关键信息提取出来，并将信息中可以计算出来的信息以数字的形式表示出来，未知信息用未知数的相关形式表示出来。初步学习不太适应的情况下，可以让学生建立表格将信息更直观地表示出来。例题：某企业于2017年初投资1000万元创建工厂，购买原材料用掉总投资的30%，采购工厂器械用掉一部分投资。其中每年购买原材料资金的30%为工厂当年的毛利润，2017年购买原材料资金的1/6为工厂当年的净利润。

（1）求2017年工厂器械折旧费;

（2）工厂于2018年初采购原材料又进行投资，数额等同于2017年采购器械的金额。2018年该工厂的净利润为84万元，求出工厂的机械每年性价比降低多少。

解析：将信息中条件充足可以明确计算出来数字的直接表示出来，如表2-1所示。

（1）很容易理清概念：2017年的机械折旧费=2017年毛利润-2017年净利润，所以很容易计算得出2017年机械折旧费90-50=40（万元）。

（2）根据第二问的已知条件，又可以提取出一些关键信息，直接将可以计算的信息用数字表示可以得出，如表2-2所示。

结合表2-1和表2-2，可以得出一条隐含信息，2018年毛利润为a×30%万元，同时根据第一问得出的机械折旧费可以找到a与x间的数量关系，即ax=40。还需要根据2018年的信息列出另一个等量关系式，2018年机械折旧费=2017年机械性价比—2018年机械性价比，可表示出为（a-40）-a（1-x）。最后根据毛利润-折旧费=净利润列出方程，即30%a-[（a-40）-a（1-x）]=84，根据两个方程组解出方程的未知数x=0.1。

三、结论

培养学生应用方程思维解决数学问题是非常重要的，但是在实际教学过程中对于方程思维模式的培养还存在一定的问题。结合多年从事数学教学的经验，本文针对现存问题提出相应的解决途径，并提出方程思维的创新性教学方法，希望能够引起更多教师的重视，在教学实践过程中针对个人特点因材施教，并注重学生的个人反馈，尽可能让学生以更轻松的方式养成方程思维。

参考文献：

[1]欧昌铬，廖启宁.基于数学核心素养的合作学习有效策略——以人教版七年级“二元一次方程组”教学为例[J].中学数学，2017（16）：8-10+13.