向量积分配律的几种证明*

毋晓迪邓艳平王宏兴

(广西民族大学 数学与物理学院,广西 南宁 530006)

0 引言

数学学科中,有很多公式和定律看似显而易见,但证明起来往往并不简单,就向量积的分配律而言,其表述为:

上述运算律表达式的证明方法和向量代数中的其他运算律的证明方法不同,并非直接根据定义来验证.根据向量具有几何与代数形式的“双重性”这一特征,本文选取向量积分配律中的第一个表达式给出四种证明方法.

1 证明向量积分配律

1.1 证法一(代数视角1)

引 理1如 果 向 量,那么

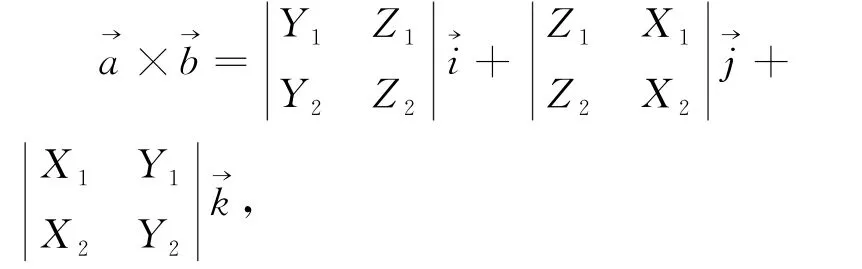
由此引理可用来证明向量积分配律,具体证明步骤如下:

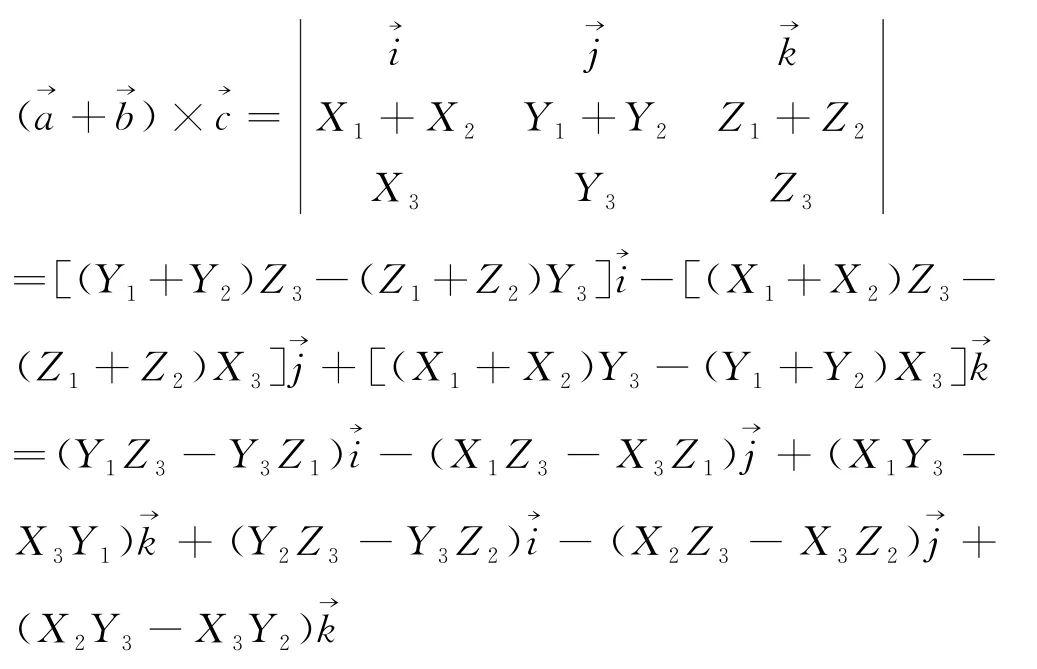
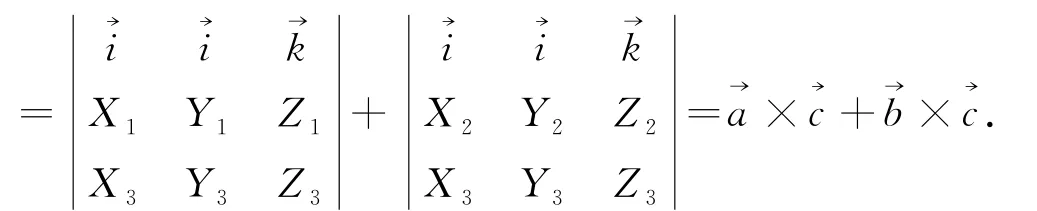
而等式左边=等式右边,即向量积的分配律得证.

1.2 证法二(代数视角2)

引理2 向量积的反交换性,即

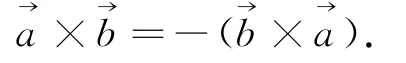
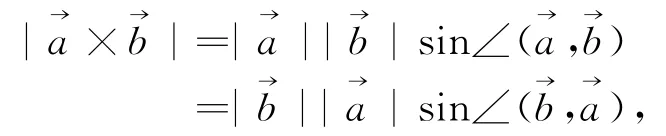
引理3 数量积(即内积、点积)的分配律,即

证明:

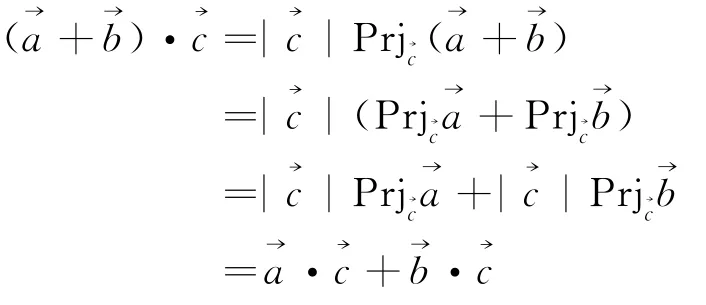
引理4 三向量混合积满足以下性质:定义为向量的混合积,常记为),则表示以为三条邻棱的平行六面体的体积,其正负号由的定向决定(右手系为正,左手系为负).

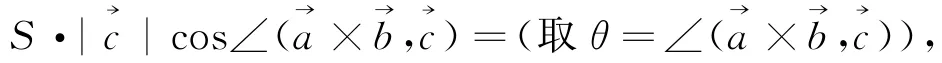
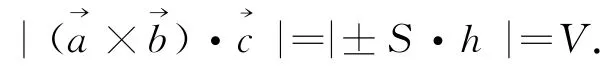
依据引理4,容易得到:

引理5 轮换混合积的三个因子,其值不改变,即

引理6 三向量混合积满足

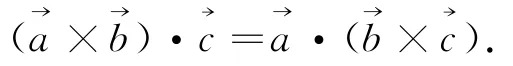
下面我们就用上面的一系列引理来证明向量积的分配律,

设为空间任意向量,构造出

1.3 证法三(几何视角1)

如图2,设平面ACC1A1,ABB1A1,BCC1B1的单位法向量分别为,则

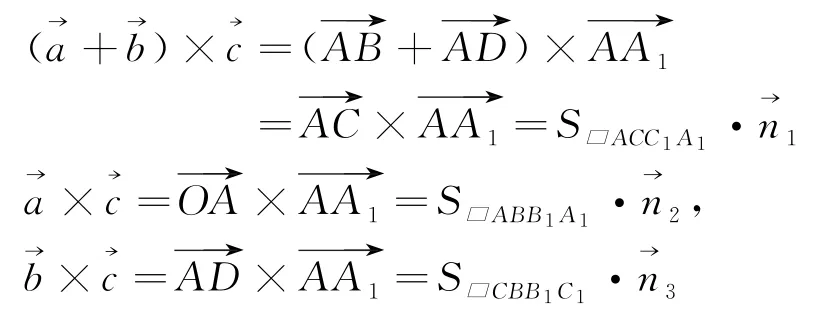
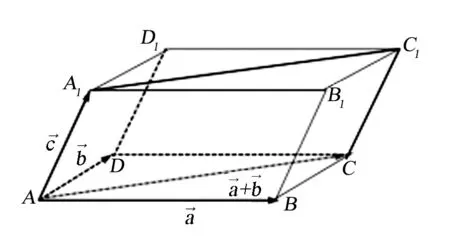
图2 三个不共面向量构成平行六面体示意图Fig.2 Schematic diagram of parallelepihedron formed by three non coplanar vectors

向量积分配律的证明可以转化为证明

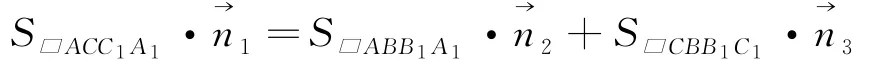
由图3可知,平面ACC1A1、平面ABB1A1与平面ADD1A1恰好围成一个三棱柱,将该三棱柱向与三条平行棱AA1,BB1,CC1垂直的平面做投影,得到的投影三角形的三边分别是原平行四边形ACC1A1,ABB1A1,CBB1C1沿水平方向所在线段的高,分别记为A0C0,A0B0,B0C0.只需证明与A0C0,A0B0,B0C0这三边等长且垂直的向量满足向量和,就能得到以面积的值为长度的垂直向量满足向量和.

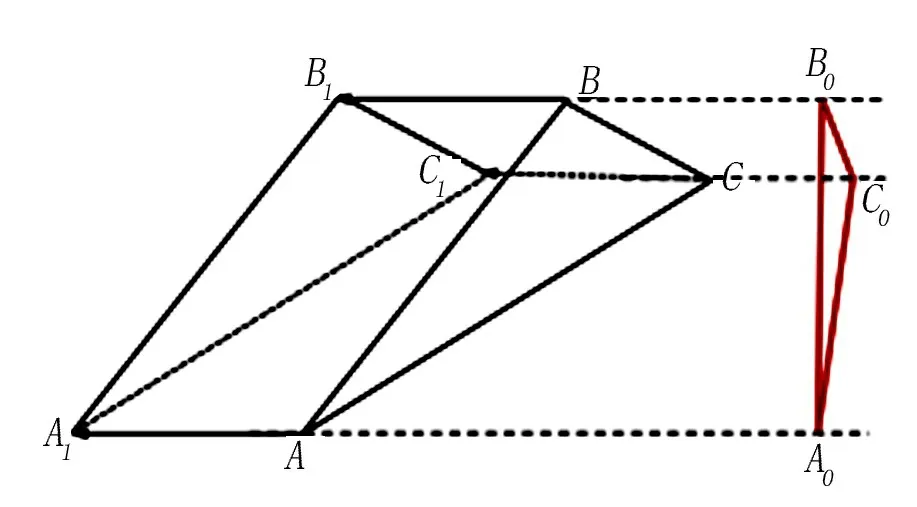
图3 三棱柱投影示意图Fig.3 Schematic diagram of prism projection

如图4,将C0B0绕B0点逆时针旋转90°得到B0C′;A0B0绕B0点顺时针旋转90°得到线段B0A′,将平移至,连接B0E、C′E,由∠A′B0C′=∠C′EA′, 而 ∠A′B0C′ =180° -∠C0B0A0,∠B0A′E +∠C′EA′ =180°, 即 △A0B0C0△B0A′E,得出:A0C0=B0E,由三角形平面旋转90°得A0C0⊥B0E.

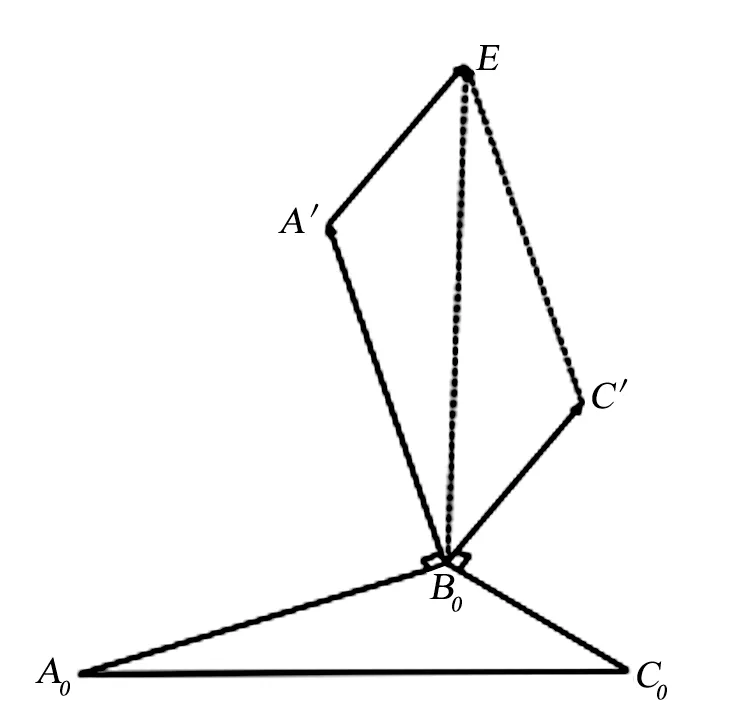
图4 向量旋转示意图Fig.4 Schematic diagram of vector rotation

而

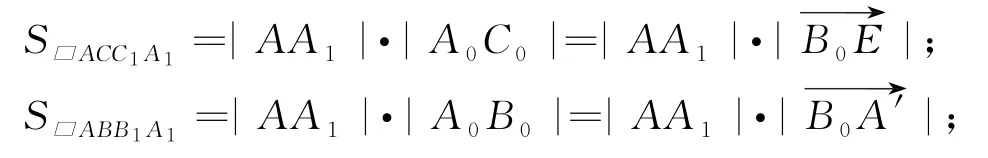
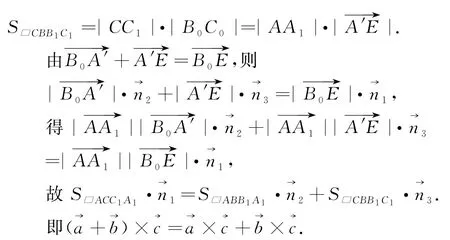
1.4 证法四(几何视角2)

在上取一单位向量,记与夹角为θ,如图5,将向量向平面α投影,投影向量记为,将向量顺时针旋转90°,得向量,由向量积定义可知:

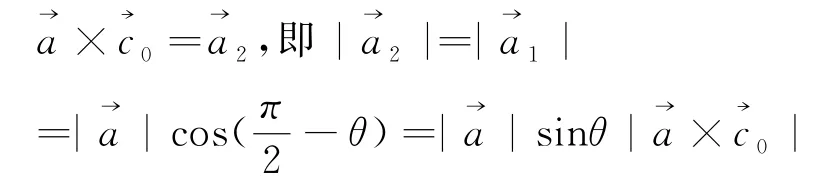
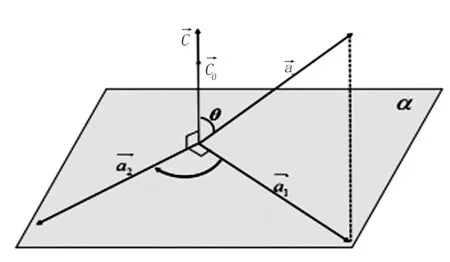
图5 向量向平面投影示意图Fig.5 Schematic diagram of vector plane projection

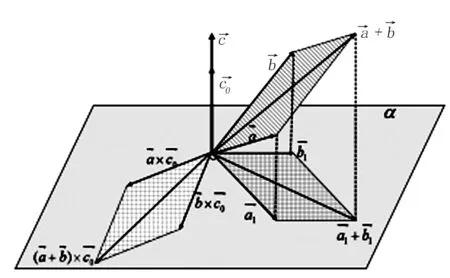
图6 向量积分配律构造平行四边形示意图(1)Fig.6 schematic diagram of parallelogram constructed by vector integral collocation(1)

再次利用向量的平行四边形法则得:

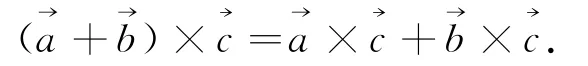
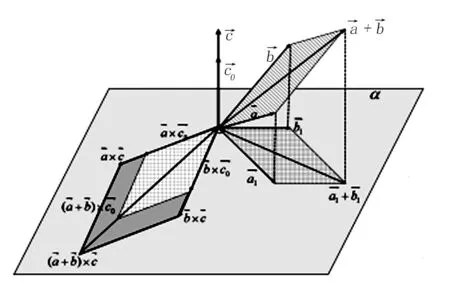
图7 向量积分配律构造平行四边形示意图(2)Fig.7 Schematic diagram of parallelogram constructed by vector integral collocation(2)

2 结语

通过翻阅大量的常规教材和教辅资料,发现对于向量积的分配律只是给出了一个简单的公式,对其为何恒成立并没有过多深入的探析.本文的四种证明方法,各有千秋,从代数角度考虑,一是从向量积的基本概念出发,严格推导,证明了分配律表达式,此外,从向量的代数特征入手,结合行列式运算推导出分配律表达式.从几何角度出发,一是通过向量叉积的几何意义构造出分配律表达式,充分诠释了转化与化归的数学思想;另外,通过旋转投影的方法顺其自然地得出分配律表达式,进而增加了新的证明视角,真正使得向量成为代数与几何之间的一座天然的桥梁.