基于智能模糊神经网络的压力机PID 控制器设计与实现*
杨 娟,龚建新
(1.百色职业学院,广西 百色 533000;2.柳州城市职业学院,广西 柳州 545036)
0 引言
压力机是一个强时变性、非线性的大型液压系统,由模拟通道输入输出元件、速度位移传感器、液压缸、先导阀、主阀等构成,系统图如图1所示.它的原理是模拟通道采集传感器传过来的速度及位置信息,传输给CPU,CPU 通过各种算法并通过D/A 模块控制比例先导阀的比例电磁铁从而控制主阀的开度,控制液压系统的液压油压力,同样的道理控制方向阀的比例电磁铁控制液压缸的速度及位置.[1-2]利用电液比例控制系统可以输出精确的控制系统流量及压力,能够自行设置速度、加速度、行程等参数,较传统的压力机控制系统能够实现更快速更高效的控制.一般采用PID 闭环控制对其进行控制,但系统的非线性、电磁阀的磁滞饱和性、液压油的压缩性等等,使得传统的PID 控制难以达到预期的理想控制效果.[3-4]近年来,专家学者对该领域进行了大量研究.其中,自正定控制算法的应用研究由于需要大量的数据支持,并对系统参数进行优化才能获得较好的控制效果,因此产生的废品量大,机器性能及评价差.自适应控制算法的利用要求对系统进行精确建模,通过完善数学推理方可实现系统模型化,但如此下来,实现难度太大.首先是不同系统对不同工艺的控制要求不同,其次是系统本身的耦合性及非线性,使得建模往往不太现实.本文提出一种智能模糊神经网络算法,利用神经网络的记忆特点自动选择各个控制阶段的控制策略,其中模糊算法降低系统的时变性与耦合性,神经网络的自学习功能可以实时对PID 参数进行快速准确的调整.[5]

图1 压力机电液比例控制系统图Fig.1 Hydraulic-electronic control system diagram of press
1 压力机液压控制系统模型描述
液压缸、液压阀和负载,决定了电液比例液压缸的动力学状态,由于系统是非线性的,这里考虑用瞬时微量状态下的动力学方程,系统在瞬时下的状态基本呈线性状态.假定液压阀是一个零开口四边滑阀,四角对称分布四个节流阀;假定在液压缸与阀之间的液压油管道尺寸足够大且对称分布,这样液压管道基本呈理想状态,内部的压力及瞬时动态基本可以忽略;液压缸只与负载产生力平衡.这样得到3个流体学及动力学方程:
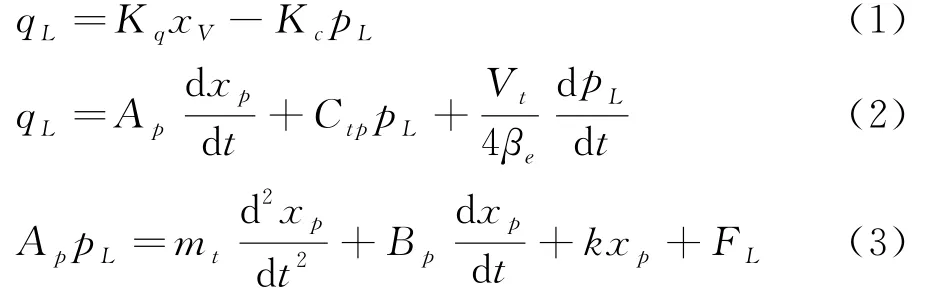
其中q L为四边滑阀的流量;K c为不同流量的压力系数;K q为四边滑阀的增益流量;P L为压力机带负载压降;A p为液压系统的液压缸的截面积;x p为液压缸内活塞的位移量;C tp为液压缸内部的泄漏系数;βe为活塞的弹性模量;V t为液压缸的总压缩容积;m t为液压缸活塞及负载在活塞上的质量;B p为黏性系数;K为负载弹簧的胡克系数;F L为外界干扰产生的额外负载力.
2 智能模糊神经网络算法
图2所示为结合RBF神经网络与模糊系统T-S模型建立的四阶神经网络系统.
整个系统由输入层、第一隐含层、第二隐含层、输出层组成.在及时获得流量控制参数情况下,电液比例控制系统的首要目的是输出平稳准确的液压油压力,关于液压压力的控制的计算方法,可以通过下面公式来表示,其中e表示压力的控制偏差,ec表示压力的变化率.
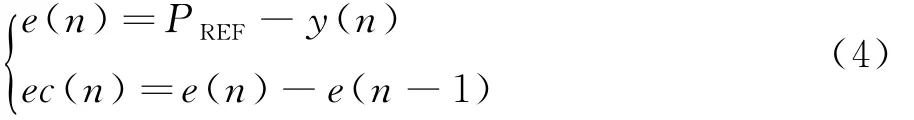
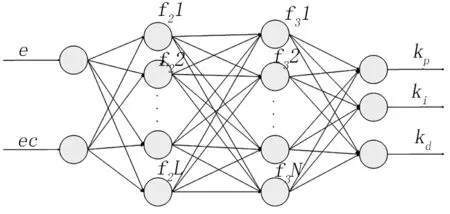
图2 RBF模糊神经网络结构Fig.2 Structure of RBF Fuzzy Neural Network
液压系统在n T时刻的压力为e(n),控制偏差即输出设定量P REF与反馈量的偏差为ec(n).[6-7]利用模糊系统优化参数,首先要将输入量进行模糊化,这里将输入量的量化等级定义为7,将其描述成模糊语言为:E的论域为[-1,1];EC的论域为[-1,1];E的模糊规则可以表示为{NB,NM,NS,ZO,PS,PM,PB};EC的模糊规则可以表示为{NB,NM,NS,ZO,PS,PM,PB}.按这个推算方法,第三层结点个数N为49个(N=7×7=49).由于节点与模糊语言一一对应,在模糊处理层,可以利用高斯型函数作为评价标准,以计算各语言变量作为隶属度程度的输入变量,从而达到模糊推理目的,公式表示如下:
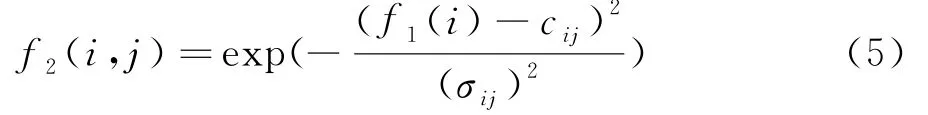
其中,σij表示第i个输入变量隶属于第j个模糊集合函数的宽度,c ij表示i个输入变量隶属于第j个模糊集合函数的中心位置.i=1,2,…,n;j=1,2,…,L.在模糊推理层中,节点与模糊推理规则也是一一对应,为了获取每个规则对于各自节点的适应度,模糊规则进行配对如下.

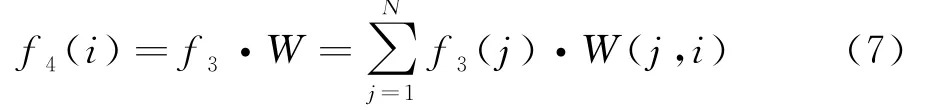
式中,W为连接权矩阵,在第四层输出层与第三层模糊推理层之间,i=1,2,3.控制器为:
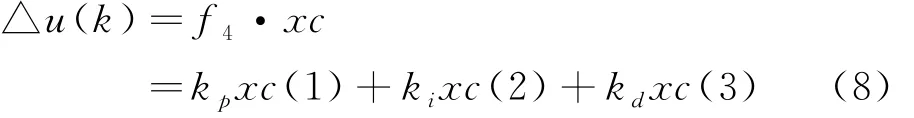
其中:k p=f4(1),k i=f4(2),k d=f4(3),xc(1)=e(k),xc(2)=e(k)-e(k-1),xc(3)=e(k)-2e(k-1)+e(k-2).以增量式PID算法作为本文液压控制系统的算法:
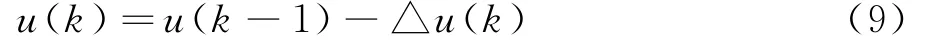
选取评价函数来对控制效果进行打分,一般可以选择控制量偏差的累积作为评价标准:

ec(t)为液压系统压力变化率;t为积分时间变量;t c为算法结束时的时间也就是积分上限时间.得到连接权W ij、中心函数c ij和宽度函数σij为:
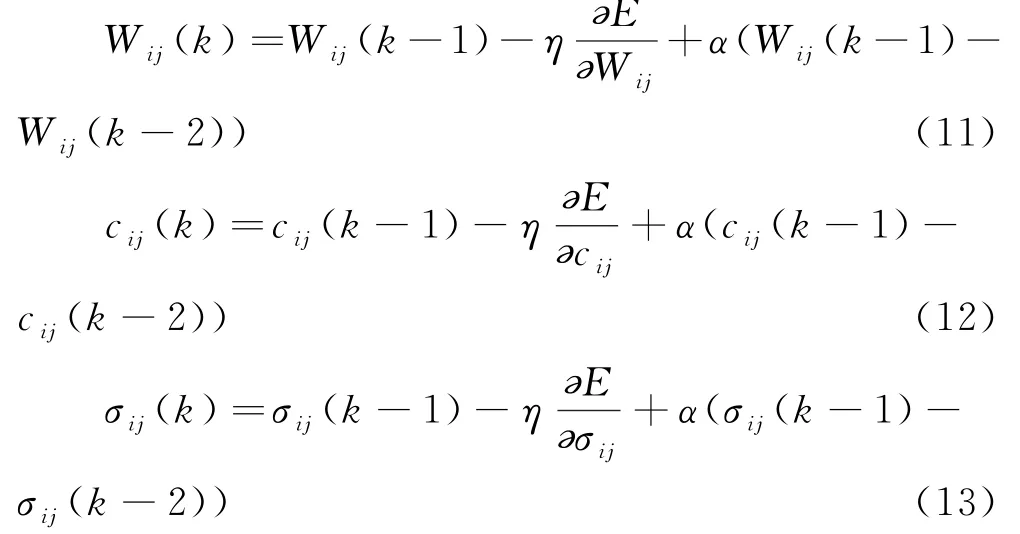
其中η为模糊神经网络算法的学习速率;α为惯性系数,0<α<1.
基于电液比例控制系统的压力机非线性和耦合性比较强,仅仅依靠模糊神经网络化PID参数优不会取得很好的效果.基于这个特殊的情况,我们引入粒子群算法对模糊神经网络的c ij、σij以及η、α参数进行再次优化.与传统的粒子群速度及位移公式不同,本文提出的速度及位移公式为:
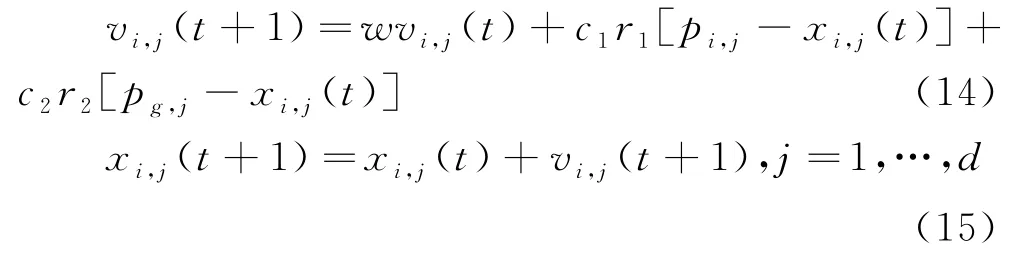
r1、r2表示随机数,取值在(0,1)之间;i表示编号为i的粒子;t表示种群的迭代次数;d表示要优化的参数,算法中为解空间的维数;c1、c2分别表示单个粒子和整个种群的加速度;w表示改良的下降幂指数惯性权重:
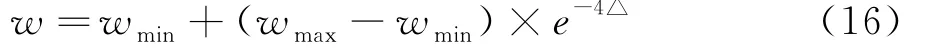
由于适应度目标函数的选取对粒子群算法的惯性权重影响较大,系统的输入包括压力变化和压力变化率,上述构建的模糊规则为7个,因此,对应的种群解空间维数为14个,每个维解都有自己的隶属度中心值和宽度,f3为中心函数c ij和宽度函数σij的适应度评价函数,由于只对中心函数和宽度函数进行优化,除了输入层到模糊化层的输入量模糊化受到影响外,其他没有变化过程,不会出现过拟合现象.
对于输出层的学习速率η和惯性系数α,由随机数产生,通过子群算法优化这两项参数,其中,E为他们的适应度评价函数.
为了验证快速收敛粒子群算的收敛速度,引入广义评价函数Griewank函数对这种改进惯性权重的算法进行收敛验证,迭代50次,得到收敛效果图如图3所示.从图中的实线与虚线可以分别观察到普通粒子群收敛情况与粒子群算法收敛速度的快慢情况.为了便于观察,我们构建如表1所示的方式计算最低收敛值情况下不同评价函数收敛次数.结合图3和表1,我们可以知道改进惯性权重后算法收敛非常明显,压力机控制的实时性大大提高.
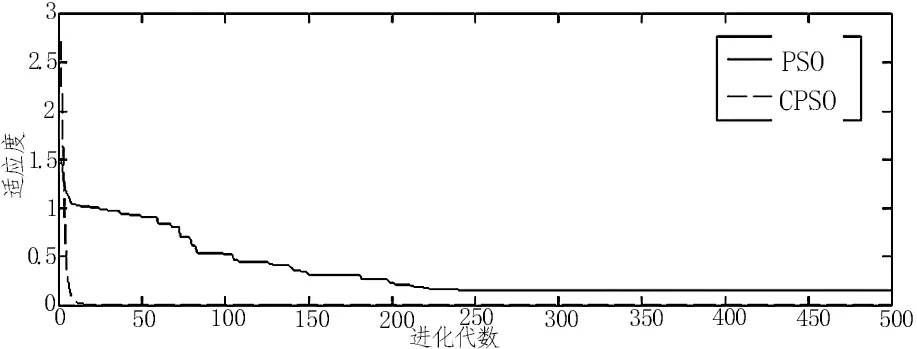
图3 Griewank 函数适应度-进化代数曲线对比图Fig.3 Fitness of Griewank function

表1 收敛迭代次数Tab.1 Number of convergence iterations
3 智能模糊神经网络压力机PID控制器设计
步骤1 对算法进行初始化,14维粒子赋予各自的初始值,算法开始没有迭代,没有办法获取全局极值,把14维空间分为e与ec两个7维.随机初始化中心函数c0和宽度函数σ0两个高斯隶属度函数,选取[0,0.5]之间的随机数赋值给η和α.
步骤2 运行算法,根据(5)~(9)式和(11)~(13)式迭代算法,在线进行优化,得到模糊神经网络的输出PID 优化结果u;
步骤3 计算每一维粒子对应的中心函数c0与宽度函数σ0适应度评价函数f3;
步骤4 对全局最优解与个体最优解进行最优化选取,得到适应度评价函数最小的粒子,用这个粒子的速度及位移替换原来公式中的速度及位移;
步骤5 利用(14)~(15)式对模糊神经网络中的中心值c ij和宽度σij进行实时优化.
步骤6 该步骤主要是通过计算系统的评价函数E获取目标函数最小的η和α,然后返回步骤2,重复该算法,直到完成规定的迭代次数为止.
4 仿真实验及结果分析
对(1)~(3)式取拉普拉斯变换,以无模多点成型压力机YAM 实际仿真模型,可以得到系统的开环传递函数为:
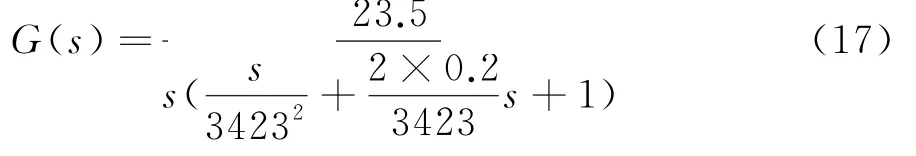
将(17)式在MATLAB平台进行仿真,压力机在初始设定的控制效果对比去曲线如图4表示,可以发现,系统的控制效果要比文献[8]提出的自校正PID控制器效果要好很多,调整时间与超调量明显减小.
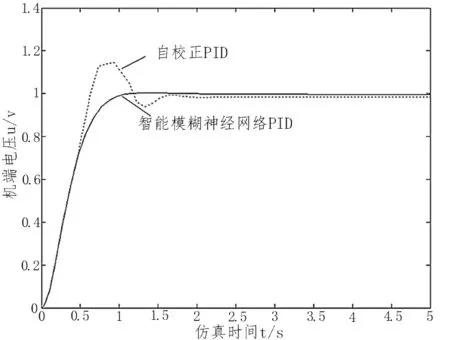
图4 智能神经网络与常规PID 定压边力初始控制曲线Fig.4 Initial control curve of intelligent neural network and conventional PID constant blank holder pressure
相对传统PID 控制算法,从表2 可以看出压力机进行定压边力的控制效果,响应时间快,控制精度高.由于压力机在压边工作过程中处于小扰动状态,系统会根据实际情况自动做出的反馈控制,通过智能模糊神经网络PID 控制器明对时间与超调量进行调整,确保响应时间小于自校正PID 闭环控制,从而可以确保压力机的稳定输出效果.
5 结语
闭式压力机液压系统的控制系统时变性、非线性比较强,在具体应用过程中,构建数学模型难度大,准确度不高.长期以来,人们基于传统PID 控制算法的控制虽然有一定突破,但达不到理想的控制效果.本文在继承传统PID 控制算法的同时,结合智能模糊神经网络算法的优势,提出一种压力机的PID 闭环控制新方法,该方法通过对快速粒子群算法改进,来对模糊神经网络算法的参数进行优化,在确保系统功能实现的同时,大大提高系统的整体性能,达到预期的控制效果,为压力机的系统性能改进与优化提供了一种新的思路.
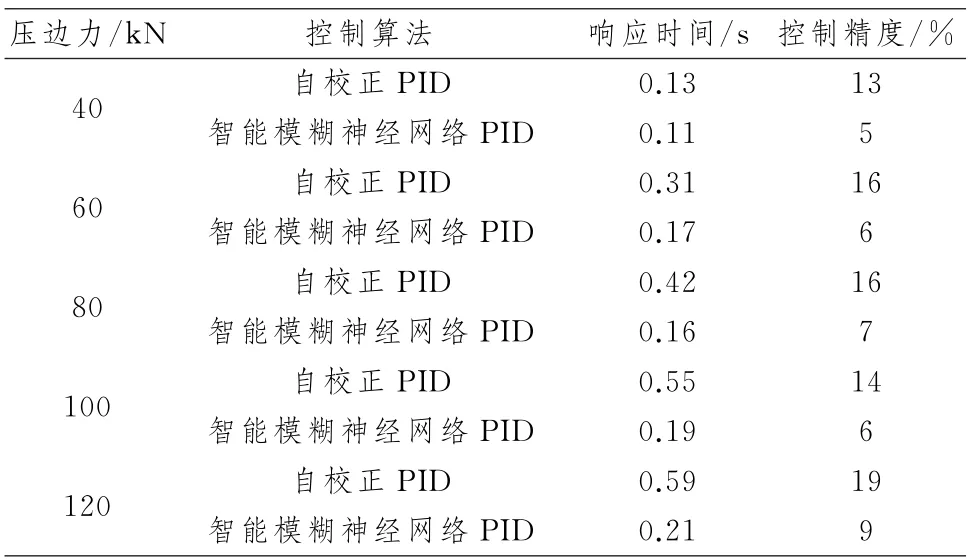
表2 系统实际控制效果对比Tab.2 Comparison of actual control effect of the system

