具有可选服务的M/G/1重试反馈排队模型的稳定性
程慧慧, 田中连
(华北水利水电大学 数学与统计学院,河南 郑州 450046)
0 引言
重试排队模型是排队论发展过程中衍生出的一类重要排队系统。近年来,具有一个阶段服务的一般重试排队模型得到广泛的关注,但在一些分布式系统控制中,服务台可能分两个阶段进行服务。在第一个阶段对传入的作业进行初步处理,如果符合某种标准,则进行第二阶段的服务。此外,两阶段服务的排队模型在计算机和通信网络中也有广泛的应用。对具有第二阶段可选服务的重试排队模型关注,KUMAR B K等[1]研究了带有优先权和两阶段服务的M/G/1重试排队模型,陈佩树等[2]研究了具有Bernoulli休假和可选服务的M/G/1重试反馈排队模型。近年来,ARIVUDAINAMBI D等[3]考虑了二次可选服务和休假的重试排队,JAIN M等[4]研究了具有两阶段服务、不耐烦顾客和阶段性修理的Mx/G/1重试休假排队,其中第二阶段有多重服务可以选择。除了对连续时间两阶段重试模型的研究,具有离散时间两阶段重试排队模型也有一些成果。WANG J等[5]研究了具有启动失败和可选服务的Geo/G/1重试排队模型,WEI C M等[6]讨论了具有不耐烦顾客和二次可选服务的离散时间的Geom/G/1重试队列。
在经过长时间的服务后,服务台可能会出现故障,从而导致启动失败,进入修理期。对于具有启动失败的重试排队模型的研究,KUMAR B K等[7]讨论了带有反馈、启动失败的M/G/1重试排队模型的性能指标。高珊等[8]考虑了有启动失败和负顾客的M~X/G/1重试排队模型。WANG J等[9]研究了具有启动失败、反馈和准入策略的M~X/G/1重试排队模型。
本文在启动失败和第二阶段可选服务的基础上,引入反馈排队机制,考虑具有启动失败、第二阶段可选服务和反馈的M/G/1重试排队模型。具有反馈机制的重试排队最早出现在分时操作计算机中。在分时计算机操作系统中,系统任务分成很多时间间隔,如果所需的总处理时间超过间隔的长度之和,信息将反馈到系统中,系统根据反馈进行下一轮工作,直至达到所需的处理时间。此外,反馈机制在通信系统中也有广泛的应用。
1 模型描述

2 系统稳定状态分析
当系统处于稳定状态时,无论初始的分布是怎样的,系统将趋于不变的概率分布。在系统稳定状态的条件下,分析系统稳定状态的性质。
2.1 系统的遍历性
采用嵌入马尔科夫链的方法对系统稳定状态条件进行分析。嵌入马尔科夫链方法的关键是嵌入点的选择。对于模型,选择嵌入点为顾客服务完成时刻或修理结束时刻。令{tn;n∈N}为第n个顾客服务完成时刻或修理结束时刻,C(tn+)为第n个顾客离开后或修理结束后重试区域的顾客数,则Xn={C(tn+),X(tn+)}形成嵌入马尔科夫链。
引理1(Forster准则)[9]一个不可约、非周期的马尔科夫链Xn是遍历的,如果存在非负函数f(j)和ε>0,使得均值偏移量xj=E(f(Xn+1)-f(Xn)/Xn=j)是有限的,并且除有限个j外几乎所有j∈N都有xj<ε。
引理2[10]一个不可约、非周期的马尔科夫链Xn是非遍历的,如果xj满足Kaplan条件,xj<∞(j≥0)并且存在自然数j0∈N,当j≥j0时,有xj≥0。

证明(充分性)显而易见,{Xn;n≥1}是一个不可约、非周期的马尔科夫链。令f(j)=j,则


2.2 队长的平稳分布
系统在任意时刻t的状态可用马尔科夫过程{C(t),N(t),ξ0(t),ξ1(t),ξ2(t),ξ3(t),t≥0}表示,其中,C(t)表示t时刻系统所处的状态,N(t)表示在t时刻重试区域的顾客数。当C(t)=0,N(t)>0时,ξ0(t)表示逝去的重试时间;当C(t)=1,N(t)≥0时,ξ1(t)表示正在进行基本服务的顾客已经逝去的基本服务时间;当C(t)=2,N(t)≥0时,ξ2(t)表示正在进行可选服务的顾客已经逝去的可选服务时间;当C(t)=3,N(t)≥1时,ξ3(t)表示逝去的修理时间。令γ(x),μ(x),ν(x),η(x)分别为重试、基本服务、可选服务和修理的条件完成率函数,则

令
P0(t)=P{C(t)=0,N(t)=0};
Pn(x,t)dx=P{C(t)=0,N(t)=n,x≤ξ0(t) Qn(x,t)dx=P{C(t)=1,N(t)=n,x≤ξ1(t) Rn(x,t)dx=P{C(t)=2,N(t)=n,x≤ξ2(t) Sn(x,t)dx=P{C(t)=3,N(t)=n,x≤ξ3(t) 根据对状态转移概率动态分析可得到 (1) (2) (3) (4) (5) (6) (7) (8) 边界条件为 (9) (10) (11) (12) (13) (14) 正则条件为 (15) (16) (17) (18) (19) (20) 平稳状态重试区域的队长分布为 (21) 证明采用概率母函数的方法求解微分差分方程(1)~(14)。首先定义概率母函数 在方程(1)~(14)中,令t→∞,即 然后方程(2)~(14)两边同时乘zn,并对n求和,可得 (22) (23) (24) (25) 边界条件为 (26) (27) (28) (29) 解方程(22)~(25),可得 (30) (31) (32) (33) 将式(30)~(33)代入式(26)~(29),可得 P(0,z)=(θ1+θ0z)β*(λ(1-z))Q(0,z)+(pz+q)V*(λ(1-z))R(0,z)+ (34) (35) R(0,z)=θ2β*(λ(1-z))Q(0,z), (36) (37) 将式(34)~(37)联合,可解得P(0,z),Q(0,z),R(0,z)和S(0,z),并将其代回式(30)~(33),并对x进行积分,即可得到定理中的(16)~(19)。令z=1,运用洛必达法则,根据正则条件P0+P(1)+Q(1)+R(1)+S(1)=1,可以得到 P0如式(20)。 平稳状态重试区域中队长的概率母函数L(z)=P0+P(z)+Q(z)+R(z)+S(z),即 除了队长的分布外,还常用忙期分布、闲期分布和平均队长作为系统性能指标的测度。 令K(z)表示系统稳定状态时顾客总数的概率母函数,由于K(z)=P0+P(z)+zQ(z)+zR(z)+S(z),由(16)~(20)计算可得 (38) 服务台的忙期是从新到达顾客发现服务台空闲,成功启动服务台开始服务时刻起,到顾客离开服务台并且重试区域没有顾客为止。服务台忙期的概率H=P(1)+Q(1),计算可得 相对于忙期分布,服务台处于空闲状态或修理状态的概率为 其中, F′(1)=αA*(λ)(1-θ0-θ2p),F″(1)=-2αλA*(λ)((θ0+θ2p)β1+θ2pν1), G″(1)=αλ(2β1(A*(λ)-θ0-θ2p-1)+2θ2ν1(A*(λ)-λβ1-p-1)-λ(β2+θ2ν2))+ 其中, M′(1)=αA*(λ)(θ1+θ2q),M″(1)=2αλA*(λ)((θ1+θ2q)β1+θ2qν1), N″(1)=αλ(2β1(A*(λ)-θ0-θ2p-1)+2θ2ν1(A*(λ)-λβ1-p-1)-λ(β2+θ2ν2))+ 随机分解定理是休假排队系统的重要性质,广泛应用于休假随机排队系统中。在休假排队系统中,任意时刻顾客数的概率母函数可以分解为以下两部分的乘积:一个是无休假系统中处于稳定状态时顾客数的概率母函数;另一个是休假排队系统中服务台处于休假状态时顾客数的概率母函数[13]。 本文考虑的模型属于无休假的排队模型,为了研究其随机分解性质,引入广义休假状态的概念。广义休假期从服务台完成任意一次服务到成功启动服务台,则系统处于广义休假状态,即系统处于空闲或修理状态。令Π(z)表示无休假、第二阶段可选服务和反馈的M/G/1排队系统稳定状态时顾客总数的概率母函数;χ(z)表示本文所考虑系统处于广义休假状态时顾客总数的概率母函数。 定理3K(z)=Π(z)χ(z)。 由(16)式可知,A*(λ)=1,则可得到 根据式(38)计算可得K(z)=Π(z)χ(z),故本文所考虑模型符合随机分解性质。 研究具有启动失败、第二阶段可选服务和反馈的重试排队模型。在稳定状态的前提下,求得系统遍历性的充分必要条件。通过求解微分差分方程得到系统中重试区域队长分布,同时得到了系统中顾客总数、忙时分布和闲时分布等一些指标,最后验证所研究模型具有随机分解性质。












Φ*(λ(1-z))S(0,z)-λP0,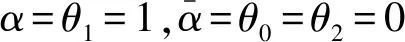
3 系统的性能指标
3.1 系统中顾客数的分布
3.2 服务台繁忙或空闲的概率
3.3 平均队长


4 随机分解定理


5 结论

