学员视角下一道第二类平面曲线积分题目的解法探讨

景慧丽, 方晓峰

(火箭军工程大学 基础部，陕西 西安 710025)

0 引言

第二类平面曲线积分[1]是多元函数积分学中一个很重要的概念，其物理意义是变力沿曲线做功，有很重要的实际应用价值[2]。计算第二类平面曲线积分常用的方法有：写出积分曲线的参数方程将其转化成定积分、利用格林公式将其转化成二重积分、利用曲线积分与路径无关的性质简化计算[3]等，当然每种方法都有自己的使用条件和适用范围。另外，有的题目可以用多种方法计算，所以第二类平面曲线积分的计算是比较开放的，当然这种开放性对培养学员的发散思维是很有帮助的。本文就一道第二类平面曲线积分题目的计算问题进行探讨，提出4种计算方法，进而培养学员的发散思维。

1 例题

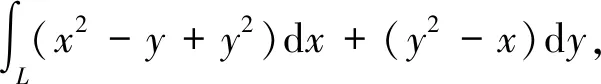
解法1先将积分路径补充成封闭曲线，再利用格林公式。

补充l1:y=0，x从-a变到a，令P=x2-y+y2，Q=y2-x，记L和l1所围区域为D，则

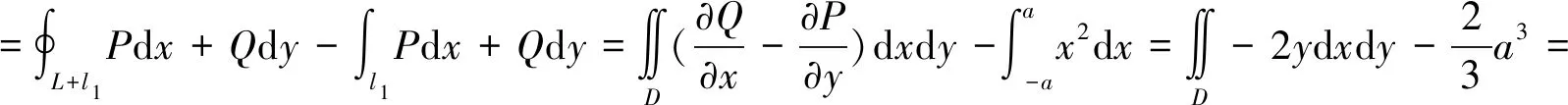
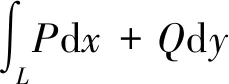
若转化为直角坐标系下先对y、后对x的二次积分，则

若转化为直角坐标系下先对x、后对y的二次积分，则

解法2先将积分曲线方程代入被积函数中，再利用曲线积分与路径无关的性质简化计算。

注3解法2利用了“可以把积分路径的方程代入被积函数中简化曲线积分的计算”这一特质，这一特质的应用把原本与积分路径有关的曲线积分转化成了与积分路径无关的曲线积分，大大简化了曲线积分的计算。计算曲线积分时可以首先考虑该特质，计算曲面积分时，也可以将积分曲面的方程代入被积函数中简化曲面积分的计算。

解法3先利用曲线积分关于被积函数的可加性,再分别利用曲线积分与路径无关的性质以及将曲线积分直接转化成定积分。因为

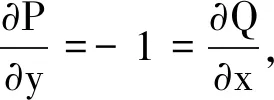
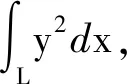
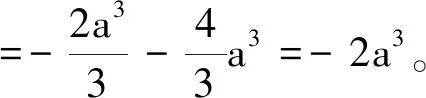
解法4写出积分路径L的参数方程，直接将曲线积分转化成定积分。

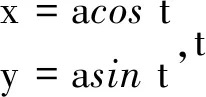
注5解法4的关键是对积分路径L的参数方程的选取，如果能巧妙地选择积分路径的参数方程，那么曲线积分的计算就会事半功倍。选取积分路径的参数方程的一般原则是：要结合被积函数的特点和积分路径的特征选取。

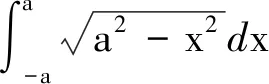
2 小结

此类第二类平面曲线积分题目的不同解法，其实很多极限、定积分、不定积分、重积分以及第二类曲面积分的题目都可以用多种思路和方法求解，在高等数学课程教学中，教员要适当地应用一题多解的题目组织教学，鼓励学员积极参与教学活动，敢于标新立异，勇于提出问题、开展交流和讨论，这样才有利于学员突破思维的局限性，培养学员的发散思维和综合能力[5-6]。