一道由积分给出的数列考研题的解法探究
王成强
(成都师范学院 数学学院,四川 成都 611130)
0 引言
数列的极限理论是大学数学的重难点内容之一。对数学领域自身而言,数列的极限理论是微积分理论的基础。在诸如生物数学、金融数学等应用领域,它往往用以建立研究对象的数学模型的数量表征[1-2]。为学好大学数学,大量的数列极限相关的问题练习必不可少[3-6]。本文旨在进一步研究2018年全国研究生入学考试数学(一)第19题,其内容完整表述如下:



1 问题1的解法探究
1.1 证明an > an+1
探究1证明不等式的常用方法是“先作差,再判断符号”。先作差,有





探究3因函数x是严格增函数,由第二型积分中值定理,故存在ξn∈(0,1),使得

注4前三种思路的共同特点是它们都依赖于Riemann积分的性质。事实上,在大学数学中,众所周知的结论是“非负函数的Riemann积分非负”,对“某Riemann积分大于零”这样的论断还是需要简单说明的。本文在引言部分给出了an基于Euler函数的表达式,这里还可尝试利用此表达式判断an与an+1之间的大小关系。


注5在探究方法4中,用到了Euler函数Γ(s)的“ln Γ(s)是严格凸函数”的这一性质:假设s1,s2>0满足s1≠s2,则对任何严格介于s1与s2之间的s,有Γ(s)<(Γ(s1))(s2-s)/(s2-s1)(Γ(s2))(s-s1)/(s2-s1)。
1.2 证明

探究6受探究5的启发,还可通过利用分部积分推导数列{an}的递推关系式。

探究7借助于分部积分法,有
注7探究5、6、7的思路都是先利用分部积分法对an作处理,再从处理之后的表达式中寻找思路。探究5的思路最为自然,但计算量稍大;探究6、7思路较“隐蔽”,但计算量较少。

探究9探究5、6、7、8都基于积分的运算。Euler函数具有丰富的性质,可尝试用来得到{an}的递推关系式。
1.3 计算极限
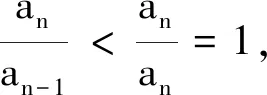

但
且
于是

探究12探究11实际上用到了Euler函数的性质。事实上,借助于Euler函数,还有下述推导过程

探究13借助于Hölder不等式,并利用数列{an}的递推关系式,有

探究14对∀ε>0,有
从而有

2 结论与思考
该结论具有推广价值。

证明利用Hölder不等式[7]可得

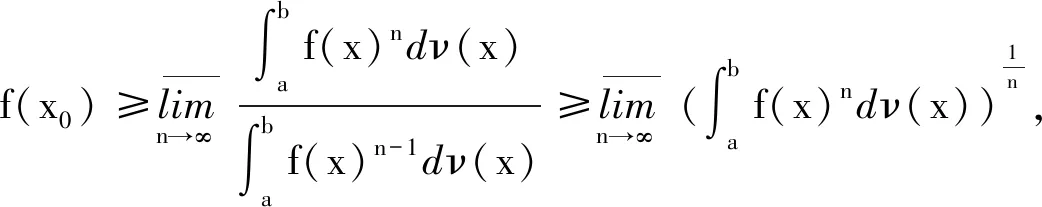
综上可知,命题1得证。

