基于运输经济模型的物流运输降本方法研究
王 昱, 石超峰
(1.重庆交通大学 交通运输学院,重庆 南岸 400074;2.重庆交通大学 经济与管理学院,重庆 南岸 400074)
0 引言
经济学理论模型已长久应用于交通运输领域,其中经典的规模经济、密度经济、网络经济模型方法更广泛适用于交通运输行业。从外文文献来看,三个经济学模型理论已经在交通规划发展指导、交通运输的优化问题研究、交通运输网路构建相关研究,以及交通经济性的评估等方面有了大量的实践应用,但研究者中却较少将其应用于交通运输相关企业的成本控制研究中[1]。企业成本控制本身就是企业经济性的体现,因此本文尝试以运输经济学模型方法进行运输企业成本控制研究。
平台型物流企业作为运输行业的一部分,运输经济学模型对其有天然的适用性,当下对物流企业的成本控制研究多采用作业成本法[2]。通过会计核算方式对企业成本的形成与企业降本增效进行决策分析,是对多数企业普适的成本控制研究方法[3]。本文通过运输经济学理论,使用对平台型物流企业降本增效相契合的经济学模型方法,即经济学经典理论,规模经济、密度经济、网络经济对涉及交通运输生产作业的物流企业通过全新视角进行降本增效研究。
1 物流运输降本的运输经济模型研究

图1 垂直降本层次示意图Fig.1 Vertical reduction hierarchy diagram
运输经济学中所阐述的规模经济、密度经济、网络经济模型,揭示了企业发展过程的客观规律[4],是对平台型物流企业降本方式选择的天然指导。以平台型物流企业运营过程中产生的数据指导企业生产运营中的降本方向,通过客观规律而非主观评价排除降本方向上的非理性因素,真实全面地展示企业成本管理中的优劣点[5]。选择规模经济、密度经济、网络经济三个模型理论,也期望从平台型物流企业的整体到局部再到企业基础层面都可以有相对应的降本模型理论进行指导,形成平台型物流企业的垂直降本体系[6],如图1所示。
如若对平台型物流企业降本模型的客观指标研究,规模经济这一展现企业生产成本变化过程的模型指标是对企业把控宏观成本的适合模型,因此本文提出第一个模型指标M1:规模经济指标是对平台型物流企业成本控制的方向把控。
使用模型为规模经济模型
C=C(Q),
(1)
AC=C(Q)/Q,
(2)
MC=dC(Q)/dQ,
(3)
Ks=AC/MC,
(4)
其中,Q:物流运输量,C:企业成本函数,AC:企业生产平均成本,MC:企业生产边际成本,Ks:规模经济指标系数。
新古典经济学派中规模经济是对企业生产过程中通过生产规模的扩大,引起的边际成本的改变而对当前生产规模产生指导性说明,边际收益是否会通过生产规模的改变而使边际成本产生有利于企业降本的方向前进。毫无疑问,边际成本是与当下生产规模(即平均成本)密不可分的,因此通过对生产数据的分析可以确定生产规模的合理性,在企业的降本决策中使降本抉择具有客观依据与说服力,对于需要降本的方式以直观结论展示,是否通过生产规模的改变达到降本目的,或通过非经营方式取得成本控制的目标。
因此规模经济通过企业自身经营数据反映企业营运的效果,在降本方式的选择中,更易于使决策者采取合适的降本方案,而不会无的放矢。从宏观层面对企业成本控制抉择提供必要的指导性信息与结论,使企业在降本过程中选择当前最有利、最高效的降本方式,避免南辕北辙而带来非必要性人力、物力的投入与大量时间的浪费。但仅有宏观降本方向的结论是不足以为平台型物流企业降本提供全部支持的。因此本文提出第二个模型指标M2:密度经济指标是对平台型物流企业成本控制的具体指导。
使用模型为密度经济模型
(5)
C2=L2·P1·Q2,
(6)
C3=L3·P2·Q3,
(7)
(8)

密度经济诞生于规模经济之后,运输经济学中的密度经济理论是通过运输生产或服务数量的重复增加对运输企业固有生产成本的摊薄,从而达到平均成本下降的目的。在企业降本增效的过程中,既有非消耗性资产、资源作为成本的一部分,无论以何种手段都无法直接消除其对企业营运成本的影响,唯有通过增加生产、服务过程频率进行均摊,才能使运输企业达到密度经济性。以平台型物流企业为例,密度经济所体现的区域站点间物流活动的频率增加,使仓库、人员开支、损耗等作为时间价值的一部分进行均摊,同时密度经济中对外包运输过程的直接费用,即运量与运输产生的时间价值,平均消耗时间组成的运输费用,直观表现出企业成本控制的重要部分——直接成本。
因此对于确定降本方向下的成本构成,密度经济模型反映了主要支出,但仍无法具体到每一个细枝末节,对于平台型物流企业而言,不同的线路、趟次、搭运货物,需要具体指出,从而提出第三个模型指标M3:网络经济指标是对平台型物流企业成本控制的细微优化。
使用模型为网络经济模型
(9)
Vr≥0,
(10)
(11)
δrm=1,
(12)
其中,Vm:起讫点OD需求,Vr:路径需求,Vl:路段需求,δrm=1:r路径流量,dlr=1:路段l在路径r上,dm(Vm):价格与成本的逆需求函数,Cl:路径阻抗函数。
网络经济原为计算机网络产生后提出以互联网为基础的经济理论,本文引申为网络的泛化概念,以交通网络下所蕴含的经济因素作为物流服务网络的网络经济模型[7]。在物流网络中,不同起讫点所组成的网络,因平台型物流企业外包物流的运输无组织性与经济学中的“理性人”特质,企业在外包物流运输网络中产生不平衡性,使物流网络中各项交通因素影响下的运输线网配流未达最优[8],在企业的基层中,产生部分成本浪费,对物流线网均衡优化达到网络均衡后,可以从基础层面达到降本效果,从而令物流运输网络的经济性达到最高[9]。
2 物流运输降本的运输经济模型研究方法设计
2.1 样本来源与数据选取
本文的降本模型研究针对平台型物流企业,在数据样本的选择中需要具有较强的针对性,同时规模经济、密度经济、网络经济的三重指标对企业的数据所包含的方面应足够全面以满足计算需求。因此选取某样本公司2013—2017年的全部运输及财务相关数据,如表1所示,以这些数据为节点进行统计及计算(用于检验模型指标M1),以细化的各业务区域数据计算(用于检验模型指标M2),以物流网络实际情况的线网优化(用于检验模型指标M3)。

表1 某物流公司样本数据/万台Tab.1 Sample data of a logistics company/10 thousand units
本文选取的数据样本应具有代表性与可利用性,在与相关公司取得联系后,使用该公司内部物流外包运输数据与相关财务数据进行统计计算,在剔除部分无效数据后,利用Excel 2010软件进行数据的处理与统计分析,使用MATLAB 7软件进行数据计算,最后以TransCAD对物流网络进行线网优化。
2.2 方法变量设定
物流作业涉及大量的经济与交通运输活动,在构建物流企业降本模型的研究中,无法刨除某一专业因素而构建模型,在降本模型的相关选择上,从与物流企业营运联系紧密的规模经济模型、密度经济模型、交通网络平衡模型、网络经济模型等着手,搭建从宏观到微观的垂直式降本分析模型,其体系应由规模经济、密度经济、网络经济等判断模型依次构成。
2.2.1 规模经济判断模型
规模经济最早由亚当·斯密在《国民财富的性质和原因的研究》进行了阐述,作为古典规模经济理论,后经马歇尔《经济学原理》的发展,在卡尔·马克思的《资本论》中总结了规模经济的实现目的:1)产供销的联合与资本的扩张;2)降低生产成本。
在对样本企业整体的经营生产状况进行评估确认的过程中使用规模经济判断模型可以确定企业生产、服务规模的合理性,反映出企业降本的潜在途径。因此使用M2规模经济判断模型,结合(1)、(2)、(3)、(4)可得
(13)
当规模经济指标Ks大于1时,即平均成本高于边际成本,企业生产、作业规模平均成本高于边际成本存在规模经济,此时,降本决策可通过扩大生产规模进行;由(13)可知,当规模经济指标Ks小于1时,即平均成本低于边际成本,企业生产、作业规模不经济,不能再扩大企业生产规模达到降本目的,应转变策略,提升管理能力、提高效率等其他措施达到降本目的。
2.2.2 密度经济判断模型
在平台型物流企业中,多将整体业务按地理区域进行划分,从而针对局部区域有效地制定区域经营策略,为区域内物流运输业务创造良好基础。在物流区域降本与密度经济理论相结合的过程中,通过密度经济的核心理念,增加既有资源的使用频率使企业成本得到下降。平台型物流企业在沟通托运方与承运方的过程中,依据目的地的不同,采用多种交通方式运输,以多式联运等方法构建区域运输模式,在降本空间中利用现有运输时间价值(value of time,VOT)对当前区域物流运输的经济性进行评估,制定降本方式方法。因此选取M2密度经济判断模型,带入(5)、(6)、(7)、(8)可得
(14)
当规模经济指标Kd高于1时,实际成本高于数据挖掘的计算成本,业务片区作业规模不经济,存在降本空间;而当规模经济指标Kd小于1时,业务片区作业规模经济,应通过管理手段产生降本空间。
模型中的时间价值是对物流企业公路运输成本的一个平均度量,通过考虑运输中驾驶人员开支和燃油消耗的直接成本与企业的延误成本,直观反映物流企业公路运输经济性,采用的时间价值构成为
VOT=Vw+Vf+Vd,
(15)
其中,Vw:驾驶人员平均小时工资水平,Vf:公路小时平均油耗折算成本,Vd:企业小时运行延误成本,其构成为
Vd=(NeW)/(Nc/24),
(16)
Ne:企业非运输雇员数量,W:企业非运输雇员平均薪金水平,Nc:物流企业公路运输载具数量。
2.2.3 网络经济判断模型
本文通过引申网络的泛化定义,在物流网络上通过网络平衡理论所达到的运输均衡的目标,实现网络的经济性,为平台型物流企业构建基层的作业指导,以此达到降本的效果。所以使用M3网络经济判断模型中(9)、(10)、(11)、(12)公式。
同时,在网络经济模型中,应通过不断地迭代达到网络的均衡性,是多因子下寻找最优解的过程,通过多次迭代使结果满足物流企业的期望值,从而达到网络经济性,产生物流网络的降本空间。
对于物流网络中的成本函数这一主要参数,选择的是美国联邦公路局使用的BPR(Bureau of Public Road)阻抗函数,反映道路运行阻抗,物流运输过程中出现在物流网中的成本是以公路运行畅顺度为依据的,因此在网络经济模型中用BPR阻抗函数作为成本函数,BPR路阻函数为
C(Q)=t0(1+α(Q/Cb)β),
(17)
其中,t0表示自由流行驶时间,Q表示实际单位小时流量,Cb表示道路设计最大小时通行能力,α和β为模型待定参数,本文取α=2.62,β=4。
本文所构建的三个模型,其中规模经济模型从平台型物流企业整体出发,以宏观视角寻找降本增效的方向;密度经济从企业内部中层出发,对局部片区的主要运输成本核算、校验,以中观的角度确定实际降本可行区域;网络经济以物流运输的基层着手,通过对既有不均衡物流网络的重新均衡,从微观视角达到降本成效。
3 物流运输降本的运输经济模型的实证与应用
3.1 规模经济判断模型
在进行规模经济判断过程中,需首先对相应数据进行拟合处理,求解出目标样本作业成本C、平均成本AC、边际成本MC,通过解析式对样本整体分析,确定样本数据呈现的态势。
表2是通过某物流公司财务及运输数据,数据的最值点于2015年产生,达到最高,而在首尾的2013年、2017年呈现较低的业务总量;同时通过业务成本的数据分析,存在成本与运输业务量的正相关变化态势。因此,这5年的运输业务总量及总成本金额上呈现的先上升后降低的变化形式与二次型函数联系密切。

表2 某物流公司业务数据量与业务成本Tab.2 Business data volume and business cost of a logistics company
在规模经济判断模型Ks下对这5年的外包业务量及其成本进行拟合,得到作业成本C、平均成本AC、边际成本MC的拟合函数结果,业务成本
C(Q)=592.241 7Q2-116 675.9Q+6 208 270.4,
(18)
业务平均成本
AC(Q)=592.241 7Q-116 675.9+6 208 270.4/Q,
(19)
业务边际成本
MC(Q)=1 184.483 4Q-116 675.9。
(20)
根据规模经济指标判断模型可得5年的业务与成本的规模经济指标系数Ks,其解析式为
(21)
规模经济指标系数Ks,在Ks>1时,即企业平均成本高于边际成本时,企业规模未达到最优,扩大生产、作业规模可以显著降低成本;而Ks<1时,即企业平均成本小于边际成本时,企业规模超过了最优节点,继续扩大生产、作用规模并不能降低成本,而会出现规模与成本同时增加的正相关态势。在此,以样本企业5年作业与成本数据拟合结果Ks,由于使用拟合解析式与原始数据有一定误差,非直接求解规模经济系数Ks,而是逆函数解析出基于5年的企业发展水平,其最佳业务规模值102.38(万台/年),即Qs≈102.38(万台/年),因此将拟合结果与5年企业的样本业务数据进行比对,如表3所示。

表3 样本业务数据与最佳规模业务量Tab.3 Sample business data and optimal size business volume
在2014至2015年企业业务扩展过快带来边际成本的显著增加,造成作业成本提升,2016年着手降本,同时控制企业自身业务规模,在2017年回归经济规模,实际样本数据部分支持了M1模型指标的可行性。
3.2 密度经济判断模型


表4 片区运输方式成本表/百万元Tab.4 Transportation mode cost/million yuan
从计算的结果中,可以发现华北与华东地区的密度经济性较低,其Kd值高于1;而其他地区均满足密度经济性,其Kd值均低于1。这个现象与地区经济活动关联密切,易发现,在中国最为发达的两个经济地区,京津冀与长三角中,由于其公路网发达,交通运输活动频繁,使公路网络的交通流运行情况长期接近于饱和流状态。公路的高度负载,造成了行程速度、燃油情况的增加,经济发达地区的人员消费水平高于其他地区,由此产生了物流运输成本的增加,反映在区域密度经济模型中即为Kd高于1的密度不经济性,而在样本企业其他业务地区由于经济及交通水平低于长三角与京津冀两个区域,使实际成本低于数据计算成本,验证了M2模型指标的可适用性。

表5 样本企业片区经营成本密度经济Tab.5 Sample enterprise area operating cost density economic
3.3 网络经济判断模型
物流运输本质是交通运输,利用公路、铁路、水路作为物流企业大量使用的运输方式[2],铁路与水路有其固有线网,只有公路运输网络可以通过优化达到降本的目的。在本文引申出的泛化网络经济中,通过对物流运输网络的优化,达到物流网络的流量均衡性,以此形成网络经济。
根据样本物流企业既有线网中的8个物流基地与9个地区中转站组成的运输网络,对其8条主要线网进行优化,通过网络经济判定模型达到网络均衡的目标,在第一轮迭代循环后达到的均衡值,如表6所示。

表6 第一次迭代运量结果Tab.6 Results of the first iteration of traffic
通过模型迭代后,原始运量在物流网络中的不均衡性,使物流运输成本增高,经过对网络的优化与均衡迭代,样本企业的运输网络达到均衡效果,实现网络的经济性,但均衡流量的下降,未达到均衡前流量值。分析发现,现有物流网络的节点与边数量较少,部分目的地的联通度低,网络径路少[10],尝试性地在网络中增加4个二级中转站M、N、O、P,并辅助现有网络进行流量均衡迭代,通过新增的4个二级中转站与原有的17个基地、目的地所构成的新的物流网络进行第二轮迭代过程预期达到Wardrop第一网络均衡值,如表7所示。

表7 第二次迭代运量结果Tab.7 Second iteration of traffic results
在加入新的网络节点后,均衡运量增加,网络经济性提高,进一步对第二次均衡后的物流网络运输时间进行计算,结果如表8所示。
第一次均衡迭代后,运输量下降,而第二次迭代,通过加入新的节点,网络的运输量相应增加,这说明,样本企业原有物流运输网络合理性较低,存在相应优化空间,以四个节点增加物流网络运量,如果深入分析,对网络全面增加细化节点[11],可以更进一步优化样本企业的物流网络,达到更优的网络经济性。
因此,在网络经济判断模型下,网络经济性不以具体数值作为标准,而是通过均衡优化使网络达到更优的经济性,第一、第二次迭代后的优化结果对比也验证了M3理论的可行性。
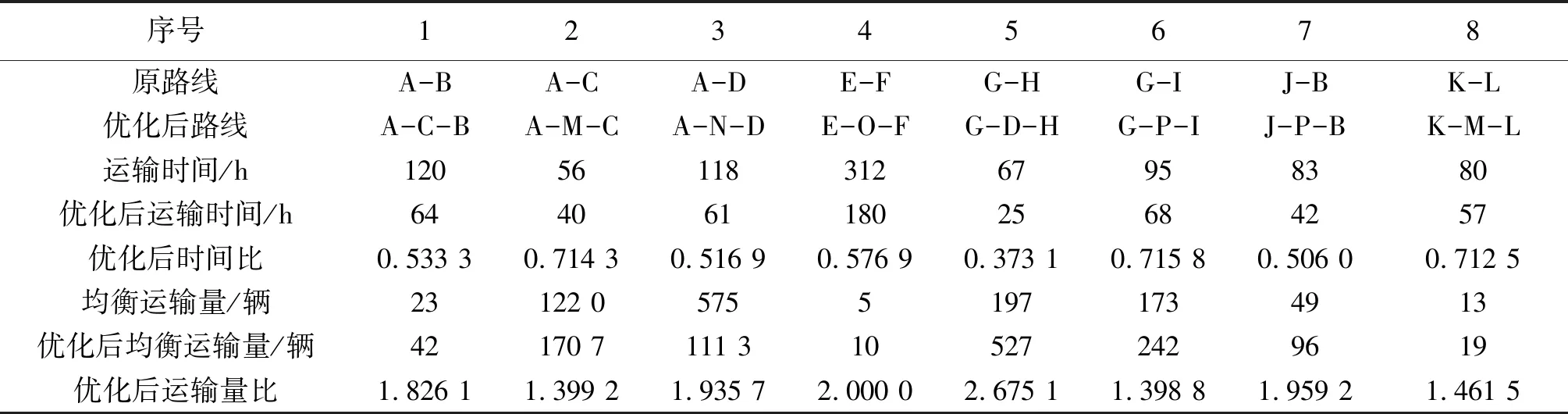
表8 第二次迭代运量、时间结果Tab.8 The second iteration of traffic and time results
4 研究结论与启示
4.1 结论
本文基于运输经济学中规模经济、密度经济、网络经济的相关理论,通过样本企业的运输与财务数据,利用规模经济模型、密度经济模型与网络均衡模型对样本企业的整体运营、片区运输成本、运输线网优化,从决策层到基础层的多维降本模型进行了分析,通过算例对研究结论进行了检验。
主要研究结论如下:
1)通过确立规模经济降本判断模型及模型指标Ks的确定方法,利用样本企业实际数据实证M1规模经济模型及Ks物流企业成本判断方法的有效性与可行性。企业整体营运数据在规模经济判定模型下可以反映企业生产、作业规模的经济性,对企业宏观降本方向的选择进行指导,判断企业是通过生产、作业的规模管控方式,还是通过企业管理效率的提升方式进行降本。
2)建立密度经济判断模型及模型指标Kd判断方法,通过样本企业片区数据验证M2密度经济模型。密度经济模型通过对片区运输数据的计算成本和实际统计成本的对比,反映区域物流运输成本控制的效果,对物流企业业务区域的运输降本方式、方法具有指导意义。
3)通过网络经济理论与网络均衡模型的优化,使物流网络整体水平、效率得到提升,验证M3网络经济模型指标。通过对样本企业现有物流网络的分析,以增加节点,多次迭代达到均衡的方式,使物流网络的运输量与运输时间相较于原始网络得到了相应的优化,达到网络经济性,在平台型物流企业降本的细枝末节上取得效果。
4.2 启示
平台型物流企业在降本的实现上,仅通过企业财务数据,可以得到需要降本的结论,但在降本的方向及降本的具体区域上无法有效把控,如能通过企业运营过程中产生的客观数据,基于相关模型,通过数据挖掘的方式,帮助相关企业在自身经营过程中找到合适的降本增效方向,对相关研究及企业自身都具有重要意义[12]。据此本文总结三点启示。
1)平台型物流企业具有相当的降本潜力。在利用样本物流企业数据进行模型计算的过程中,从整体的运输、财务数据到片区的计算成本及最后的物流线网的优化过程,都具有一定的降本潜力,尤其在物流企业的基础线网运输过程中,大量点对点的直接运输,在引入部分中转和相近目的地联合运输后,运输量与运输时间都有了较大的提升,如若能对平台型物流企业物流具体线网进行全面优化,企业的降本潜力将被完全挖掘出来。
2)从宏观到微观的垂直降本体系。平台型物流企业在进行降本的过程中,从企业决策层到片区负责人及至具体的运输者,基于规模经济、密度经济、网络经济从宏观到微观的逐步深入、细化的理论模型。
平台型物流企业通过不同理论模型对应的内部层级,使用合适的模型,达到不同层面同时进行降本;多层次的降本规划,对各个层级的工作人员都能起到有效的指导作用,基础层面的具体线路优化、片区的成本核算以及总部高层的降本方向确定,以形成多维一体的降本体系。
3)平台型物流企业降本的可持续性。对于物流企业,其生产、作业是持续的、不间断的,形成的企业营运数据也是连续性的。依据近年数据,通过模型计算所得到的结论是对过去的总结,对现今的指导,历史数据并不与企业实时运行密切相关,所以笔者希望通过构建起平台型物流企业的降本模型方法体系,为相关企业实施降本提供理论支撑与参考依据,在企业的运作中,通过不断地使用更新的相关数据,进行降本的相关计算,持续为平台型物流企业提供其降本的最新变化,同时直观地反馈已得到的降本效果,从而形成降本的持续性。

