正定矩阵的性质研究及应用

李绍刚, 迟晓妮

(1.桂林电子科技大学 数学与计算科学学院，广西 桂林 541004;2.广西高校数据分析与计算重点实验室，广西 桂林 541004)

0 引言

正定矩阵是一类特殊且重要的矩阵类型，在最优化控制、几何学、概率论、计算机图形学等学科中有着广泛的应用，文献[1-5]对正定矩阵在单调性、凸性、等价性以及合同对角化方面做了研究和探讨，文献[6]对正定矩阵的行列式的不等式进行了研究。

本文对正定二次型的判定方法进行研究，并对其性质进行了推广, 利用同时合同对角化的结论对正定性的相关命题进行了研究，并给出正定性的不等式应用，举例说明了应用的情况。

1 基本引理

首先给出正定矩阵证明中常用的几个基本结论，这些结论在定理证明中有重要应用。

引理1[7]已知x≠0∈Rn，

1)若A是n阶矩阵，且|A|≠0，则Ax≠0;

2)若B是m×n的实矩阵，且r(B)=n,则Bx≠0。

引理2设A是m阶正定矩阵，B是m×n的实矩阵，证明：BTAB正定的充要条件是r(B)=n。

证明因为 (BTAB)T=BTATB=BTAB，故BTAB是实对称矩阵。

(充分性)对任意x≠0∈Rn，因为r(B)=n，由引理1 可知Bx≠0， 注意到A是m阶正定矩阵，则有(Bx)TA(Bx)=xTBTABx>0,故BTAB正定。

(必要性)因为BTAB正定， 所以对任意x≠0∈Rn，有xTBTABx=(Bx)TA(Bx)>0, 又依题设，A为正定矩阵，则由正定的定义要求可知Bx≠0，即除非x=0才有Bx=0，故r(B)=n。 必要性也可这样证明：由BTAB正定可知r(BTAB)=n, 从而可得

n=r(BTAB)≤r(B)≤n,

即证r(B)=n。

由该引理不难得到下列结论成立。

1)若A为n阶实矩阵，则A可逆的充要条件是矩阵ATA正定。

2)设Am×n为实矩阵, 则线性方程组Am×nx=0只有零解的充要条件是矩阵ATA为正定矩阵。

引理3设A为n阶实对称矩阵，B为n阶正定矩阵，则存在n阶可逆矩阵P使得

PTBP=E,PTAP=Λ。

其中Λ为对角形矩阵。

PTBP=E,PTAP=Λ。

引理4[7]设A∈Rn×n, 则下列结论互相等价：1)A为正定矩阵； 2)A与单位矩阵E合同；3) 存在可逆矩阵P，使得A=PTP;4) 存在列满秩矩阵B∈Rm×n,使得A=BTB;5) 存在正定矩阵B,使得A=B2;6) 存在正定矩阵B与k≥1，使得A=Bk;7)A的特征值全为正数。

引理51)若A为n阶正定矩阵，B为n阶实对称矩阵，则AB的特征值为实数；

2)若A为n阶正定矩阵，B为n阶半正定矩阵，则AB的特征值为非负实数。

证明1)由A正定矩阵和引理4可知A=C2，其中C为正定矩阵。于是

AB=C2B=C(CTBC)C-1,

B为实对称矩阵和引理2可知CTBC也为实对称，从而特征值为实数。上式表明AB与CTBC相似, 从而有相同的特征值，所以AB的特征值为实数。

2)接上面，当A为n阶正定矩阵，B为n阶半正定矩阵，CTBC也为半正定，从而特征值为非负实数，进一步得AB的特征值为非负实数。

2 正定性质的推广

定理1设A,B均为n阶正定阵，证明：AB正定的充要条件是AB=BA。

证明(必要性)因为AB为正定矩阵，则AB=(AB)T=BTAT=BA。

(充分性)因为AB=BA，故(AB)T=(BA)T=ATBT=AB，故AB为对称矩阵。因为A为n阶正定阵，故可令A=C2，其中C为n阶正定阵，于是C-1ABC=C-1C2BC=CBC=CTBC，从而AB与CTBC相似，具有相同的特征值，又因为B为n阶正定阵，故CTBC为n阶正定阵，其特征值全为正数，所以AB的所有特征值全为正数，故AB正定。

定理2设A,B,A-B均为n阶正定矩阵，且AB=BA，证明：矩阵A2-B2为正定矩阵。

证明(方法1) 依题意知AT=A,BT=B,而A,B均为n阶正定阵，则A+B为正定矩阵，又因A-B为正定矩阵，且AB=BA，从而A2-B2=(A+B)(A-B)=(A-B)(A+B) ，从而由定理1可知矩阵A2-B2为正定矩阵。

(方法2) 因A,B为正定矩阵，所以A+B正定，因此存在可逆矩阵C，使得A+B=CTC，又因AB=BA，故A2-B2=(A-B)(A+B)=C-1C(A-B)CTC, 因此A2-B2与C(A-B)CT的特征值相同，且后者与A-B的特征值同号，又A-B正定，因此A2-B2的所有特征值全大于零，而A2-B2是对称阵，故A2-B2正定。

定理3设A为n阶可逆实对称矩阵，证明：矩阵A正定的充要条件是对于任意的n阶正定矩阵B，tr(AB)>0,其中tr(·)表示方阵的迹。

证明(必要性)因为A正定，由引理4可知存在正定矩阵C，使得A=C2, 故可得C-1ABC=C-1C2BC=CBC=CTBC,即AB与CTBC相似，而B正定，从而CTBC正定，即CTBC的特征值都大于零，从而AB特征值都大于零，即tr(AB)>0。

(充分性)由于存在正交矩阵P，使得PTAP=diag{λ1,λ2,…,λn}，其中λi≠0,i=1,2,…,n是A的特征值。令B=Pdiag{1,t,…,t}PT,00。 同理可证λi>0,i=2,3,…,n。 即A正定。

3 正定性的应用

3.1 特征值和方程根方面的应用

定理4设A为n阶实对称矩阵，其特征值满足λ1≤λ2≤…≤λn，则有∀X∈Rn，有λ1XTX≤XTAX≤λnXTX。

证明因为A为n阶实对称矩阵，故存在正交矩阵T，使得TTAT=T-1AT=diag{λ1,λ2,…,λn}=Λ,于是T-1AT-λ1E的特征值非负，故A-λ1E半正定，从而XT(A-λ1E)X≥0，即λ1XTX≤XTAX。 类似可证XTAX≤λnXTX。从而λ1XTX≤XTAX≤λnXTX。

推论1令c≥max{|λ1|,|λ2|,…,|λn|}>0，则∀X∈Rn有|XTAX|≤cXTX。

定理5设A,B均为n阶实对称矩阵且B为正定矩阵，则有

1)|λB-A|=0的根全是实数；

2)设|λB-A|=0的根为λi(i=1,2,…,n)且满足λ1≤λ2≤…≤λn，则

且f(X)=XTAX在约束条件XTBX=1下的最小值和最大值分别为λ1,λn。

证明1)因为B为n阶正定矩阵，A为n阶实对称矩阵，故由引理3可知存在n阶可逆矩阵P,使得

PTBP=E,PTAP=Λ=diag{λ1,λ2,…,λn},

且λi(i=1,2,…,n)是实数， 从而|λB-A|=0等价于|PT(λB-A)P|=0, 由 |P|≠0，可以约去|P|2，即得(λ-λ1)(λ-λ2)…(λ-λn)=0，故|λB-A|=0的根λ=λi(i=1,2,…,n)全是实数。

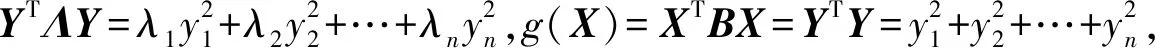
方法2由XTBX=1，故XT(PT)-1P-1X=1, 令P-1X=(y1,y2,…,yn)T，则

f(X)=XTAX=XT(PT)-1ΛP-1X=YTdiag{λ1,λ2,…,λn}Y=

同理可证f(X)≤λn。

推论2设A,B均为n阶正定矩阵，证明：1)|λB-A|=0的根全是正数；2)AB正定的充要条件是AB=BA。

证明1)类似于定理5的证明，从略。

2)充分性。因为A,B均为n阶正定矩阵，故AT=A,BT=B，又因为AB=BA, 所以(AB)T=BTAT=BA=AB，从而AB为对称矩阵；注意到A,B正定，所以A-1也正定，从而由1)可知|λA-1-B|=0的根全大于0，即|λE-AB|=0的根全大于0，这说明AB的特征根全大于0， 故AB为正定矩阵。 必要性与定理1相同。

例1设A,B均为n阶正定矩阵，且存在实可逆矩阵P，使得PTAP=E,PTBP=Λ=diag{λ1,λ2,…,λn}。证明：1)λ1,λ2,…，λn是矩阵BA-1的全部特征值；2)A-B正定的充要条件是对于BA-1的每一个特征值λ，有|λ|<1。

证明1)一方面，由已知条件可知，|λA-B|=0等价于|PT(λA-B)P|=0，即 |λE-Λ|=0 ；另一方面，|λA-B|=0等价于|(λA-B)A-1|=0，即 |λE-BA-1|=0，从而λ1,λ2,…，λn是矩阵BA-1的全部特征值，证毕。

2)PT(A-B)P=diag{1-λ1,1-λ2,…,1-λn}，即A-B合同于对角阵diag{1-λ1,1-λ2,…,1-λn}，由正定矩阵的特征值均大于零可得|λ|<1。

例2(北京化工大学2014年考研题)设A,B均为n阶实对称矩阵，且A为正定矩阵，B为负定矩阵，证明：多项式f(λ)=|B-λA|=0的根全是负实数。

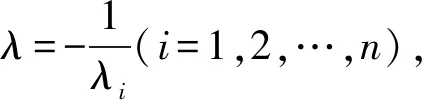
例3(上海大学2015年考研题)设A,B均为n阶实对称矩阵，且A为正定矩阵，多项式f(λ)=|λA+B|=0的根全是正数，证明：B为负定矩阵。

证明由A为正定矩阵，B为实对称矩阵 ，由引理3可知，存在可逆矩阵P，使得PTAP=E,PTBP=Λ，其中P=P1P2。

3.2 不等式方面的应用及推广

定理6设A,B均为n阶正定矩阵，证明：|A+B|>|A|+|B|。

推论3设A为n阶正定矩阵，B为n阶半正定矩阵，则|A+B|≥|A|+|B|。

利用上述推论易证下列结论成立。

1)设A为n阶正定矩阵，E为n阶单位矩阵，则有|A+E|>1;

2)设A为n阶正定矩阵，则有|A+2E|>2n;

3)设A为n阶半正定矩阵，则有|A+2019E|≥2019n，等号成立当且仅当A=0;

4)设A为n阶正定矩阵，B为实矩阵并且0不是B的特征值，则有|A+BTB|>|A|。

证明由引理3可知存在实可逆矩阵P使得A=PTEP,B=Λ=PTdiag{λ1,λ2,…,λn}P，|λB-A|=0的根λ1,λ2,…,λn全是正数。 从而可得

|A+B|=|P|2(1+λ1)(1+λ2)…(1+λn)， |A|=|P|2，|B|=|P|2λ1λ2…λn，

结论成立只需证明下列不等式成立

上述定理7和定理8的证明均由引理3进行转化为相关不等式的证明。

定理9(阿达玛定理1893)

定理10[6]若A=(aij)n是n阶正定矩阵，假设α,β是给定的指标集(是集合{1,2,…,n}的一个子集)，令A(α)表示A的一个子矩阵(A的行列取法由α确定)，如果α为空的，记A(α)=1，则有

1)Hadamard-Fischer不等式：|A(α∪β)|≤|A(α)||A(β)|。

正定矩阵的不等式也是现阶段的一个研究重点，可以结合Kantorovich、Jessen不等式和矩阵的谱理论进行深入研究。

4 结论

本文总结了正定矩阵的基本性质，并推广其部分性质，研究了这些性质在相关题目中的一些应用以及正定矩阵行列式的不等式公式及相应的推广。