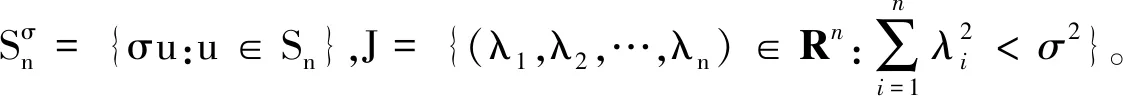一类四阶椭圆方程的无穷多个解的存在性
陈玉松, 李 晨
(商丘工学院 基础教学部,河南 商丘 476000)
1 预备知识和主要定理
考虑四阶椭圆方程
其中Δ2:=Δ(Δ)是双调和算子。
由于四阶椭圆方程在物理学和工程学的许多实际问题中,有着重要的意义,很多学者对这类方程的解的存在情况产生了浓厚的兴趣。起初,很多作者主要研究的是在有界光滑区域上该系统的解的存在情况,类似的文章可见文献[1-3]。许多学者把有界光滑区域扩展到了空间RN,陆续得到了很多好的结果[4-6]。对于整个空间RN的情景,索伯列夫紧嵌入的丢失导致问题变得困难。为了克服这个困难,很多学者对势能V做了适当的假设[4-5]。特别地,文献[6]在势能泛函满足局部紧的条件下,利用变分原理得到了超线性四阶椭圆方程的非平凡解的存在性和多重性。对于次线性的情况,文献[5]利用临界点理论中的对称山路定理得到了无穷多个非平凡解的存在性。受前人的启发,本文主要考虑的是一类次线性四阶椭圆方程的无穷多个非平凡解的存在性。为了简化讨论,作如下假设:
(V1)V(x)在RN中是连续的,且V(x)≥0。
(V2) 至少存在正常数b,满足集合Vb:={x∈RN|V(x) 定理1假设条件(V1,V2)和(F1,F2)都成立,则至少存在一个非平凡解。则在H2(RN)中该方程至少存在一个非零周期解。 定理2假设条件(V1,V2)和(F1,F2)都成立,且泛函f满足下列条件: (F3) 对于任意的(x,u)∈RN×R,有f(x,-u)=-f(x,u), 则方程存在无穷多个非平凡解。 更多地, 设泛函 (1) 通过一般的讨论,很容易验证I(u)∈C1(E,R),且 (2) 更多地,泛函I在E上的临界点恰是该系统的解。为了得到我们的结论,给出以下引理。 为了得到泛函I的非平凡临界点的多重性,在下面的证明中将用到临界点理论中的“属”属性。设X是一个巴拿赫空间,I∈C′(X,R),C∈R。集合∑={A⊂X-{0}:A是闭集且关于0对称},Kc={u∈X:I(u)=c,I′(u)=0},Ic={u∈X:I(u)≤c}。 定义[8]对任意的A∈∑,若在C(A,Rn{0})上存在一个奇函数,且n是这个属性中的最小整数。 第一步:验证I是下方有界的。由(2),(F1)以及Hölder不等式,可得 (3) 由于1 第二步:验证I满足(PS)条件。 (4) (5) 由(5)式可知,存在n0∈N,满足 (6) 因此,由(F1)、(3)式、(6)式以及Hölder不等式,可得 (7) 另外,由条件(3)、(4)以及(F1),可得 (8) 由于ε是任意的,结合(7)和(8),当n→∞时可得 (9) 由(4)和(9)可知,当n→∞时有 成立,从而在空间E中有un→u0成立。因此验证了泛函I满足(PS)条件。 其中,1 由定理1的证明可知,I∈C1(E,R)是下方有界且满足(PS)条件的。另外由条件(F3)和(3),可验证I是偶函数,且I(0)=0。为了利用引理2, 下面证明对于任意的n∈N,存在ε>0,满足 γ(I-ε)≥n。 (10) (11) 因此 (12) 且 (13) 故存在一常数C2>0,对于任意的u∈En满足 C2‖u‖E≤‖u‖r3。 (14) 由(3),(11)~(14)和(F3)对于u∈Sn,有 (15) 由1 I(σu)<-ε。 (16) (17)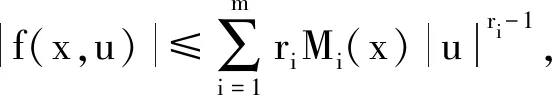
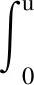
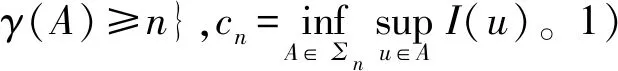
2 定理1的证明

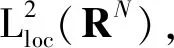
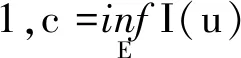
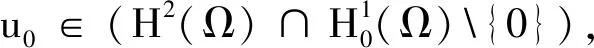
3 定理2的证明