具有两个备用服务台的异步限制休假排队
,,
(1.安徽信息工程学院,安徽 芜湖 241000;2.江苏大学,江苏 镇江 212013)
现实生活中,休假期间也会有顾客到达,鉴于工作休假的研究[1,2],在休假期内引入备用服务台上岗工作,会更好地兼顾系统服务及休假期内设置辅助工作两者的效益.马金旺,胡彬等[3,4]将备用服务台引入单服务台休假排队系统中,具有很好的实际效果.而服务台同步休假[5,6]要求所有服务台需在空闲一定数量的条件下同步进入休假,从而造成资源的浪费,故异步休假[7,8]更适合实际应用.基于此,提出了具有两个备用服务台的异步限制休假排队.
1 具有两个备用服务台的异步限制休假排队
1.1 模型描述
1) 顾客到达均为泊松到达,到达率为λ,服务机制为FCFS.
2) 系统设有5个标准服务台和2个备用服务台.服务时间均服从负指数分布,服务率分别为u1和u2,u2 3) 标准服务台完成某项服务,若遇系统中有顾客等待,则继续为下个顾客服务;若遇系统中无顾客等待,可能出现两种情形: i.系统中处于休假的标准服务台数小于2 h,该标准服务台休假,由一个备用服务台替换工作. ii.系统中处于休假的标准服务台达到2 h,该标准服务台不能休假进入空闲状态. 4) 若一个标准服务台结束休假时系统无顾客等待,就开始另一次独立同分布的休假,若系统有顾客等待则休假结束,若此时系统中有顾客正被备用服务台服务,则备用服务台立刻中止服务且已服务的时间无效,标准服务台对该顾客重新开始服务,备用服务台转为备用. 5) 标准服务台休假时间V服从参数为θ的指数分布,备用服务台不休假. 以上随机变量均相互独立. Lv(t)表示时刻t系统内顾客数,J(t)表示时刻t正在休假的标准服务台数(即工作的备用服务台数).{Lv(t),J(t)}是一个QBD(拟生灭过程),有状态空间 Ω={(k,2):0≤k≤3}∪{(4,j):2≥j≥1}∪{(k,j):k≥5,0≤j≤2} J(t)=0表示所有的服务台都是标准服务台,J(t)=2表示2个备用服务台全在工作. 系统的状态转移情况如图1所示. 图1 模型的状态转移图 将状态按字典排序,过程的无穷小生成元可写成以下三对角分块矩阵的形式 其中A0=-λ,A1=-(λ+u1),A2=-(λ+2u1),A3=-(λ+3u1), 引理1 代数方程 [(3+k)u1+(2-k)u2]z2-[λ+(3+k)u1+(2-k)u2+(2-k)θ]z+λ=0,0≤k≤2 (1) 证明:采用文献[9]的方法,设a=(3+k)u1+(2-k)u2,b=(2-k)θ, 由于方程根的判别式 Δ=(λ+a+b)2-4aλ=(λ-a)2+2λb+2ab+b2>0 当k=2时,5u1z2-(λ+5u1)z+λ=0,可得r22=λ(5u1)-1=ρ<1,r22*=1. 定理1ρ=λ(5u1)-1<1时,矩阵方程R2B+RA+C=0 (2) 有最小非负解 (3) 其中r00,r11,r22=ρ是方程(1)在(0,1)内的根. 证明:将A,B,C,R代入(2)式,整理后可得 {(3u1+2u2)r002-(λ+3u1+2u2+2θ)r00+λ=0 (4u1+u2)(r00r01+r01r11)+2θr00-(λ+4u1+u2+θ)r01=0 5u1(r00r02+r01r12+r02r22)+θr01-(λ+5u1)r02=0 (4u1+u2)r112-(λ+4u1+u2+θ)r11+λ=0 5u1(r11r12+r12r22)+θr11-(λ+5u1)r12=0 5u1r222-(λ+5u1)r22+λ=0 (4) 从而定理得证. 当ρ<1时,(Lv,J)表示过程(Lv(t),J(t))的稳态极限.记 定理2 当ρ<1时,(Lv,J)的分布可表为: (5) 其中β0,…,β5是方程组(π02,π12,π22,π32,(π42,π41),(π52,π51,π50))B[R]=0的正解,常数因子可表为: 证明:先求B[R]及正左不变向量(π02,π12,π22,π32,(π42,π41),(π52,π51,π50)), 代入方程组可 典无休假M/M/5的等待顾客数,附加队长Qd有PGF(概率母函数) 常数σ可表示为:σ=β50+δ(I-H)-1ξ. 证明:将R和β5的分块表示代入πk=Kβ5Rk-5,k≥5,可得: 于是,条件随机变量Qv(5)的分布可表示为: (6) 对(6)取PDF,我们有 定理4ρ<1时,对条件等待时间Wv(5)可随机分解为Wv(5)=W0(5)+Wd,其中W0(5)对应经 典无休假M/M/5的条件等待时间,附加延迟Wd有LST: 于是Wv(5)的LST可计算如下: 由定理3和定理4的随机分解结果,可给出下列均值公式: 取λ=0.7,θ=0.3,u1分别为0.5,0.6,0.7,得到平均附加队长和平均附加延迟随备用服务台的服务率的变化情况图2与图3所示. 图2 平均附加队长随备用服务员服务率的变化 图3 平均附加延迟随备用服务员服务率的变化 在5个服务台异步休假排队系统的基础上引入2个备用服务台,利用拟生灭过程和矩阵几何解得方法给出了在服务台全忙条件下队长和等待时间的条件随机分解,以及忙期的概率,平均附加队长的母函数和附加延迟的LST,并通过MATLAB刻画出备用服务率以及休假策略对系统的影响,为实际中出现此类模型的研究提供了理论依据.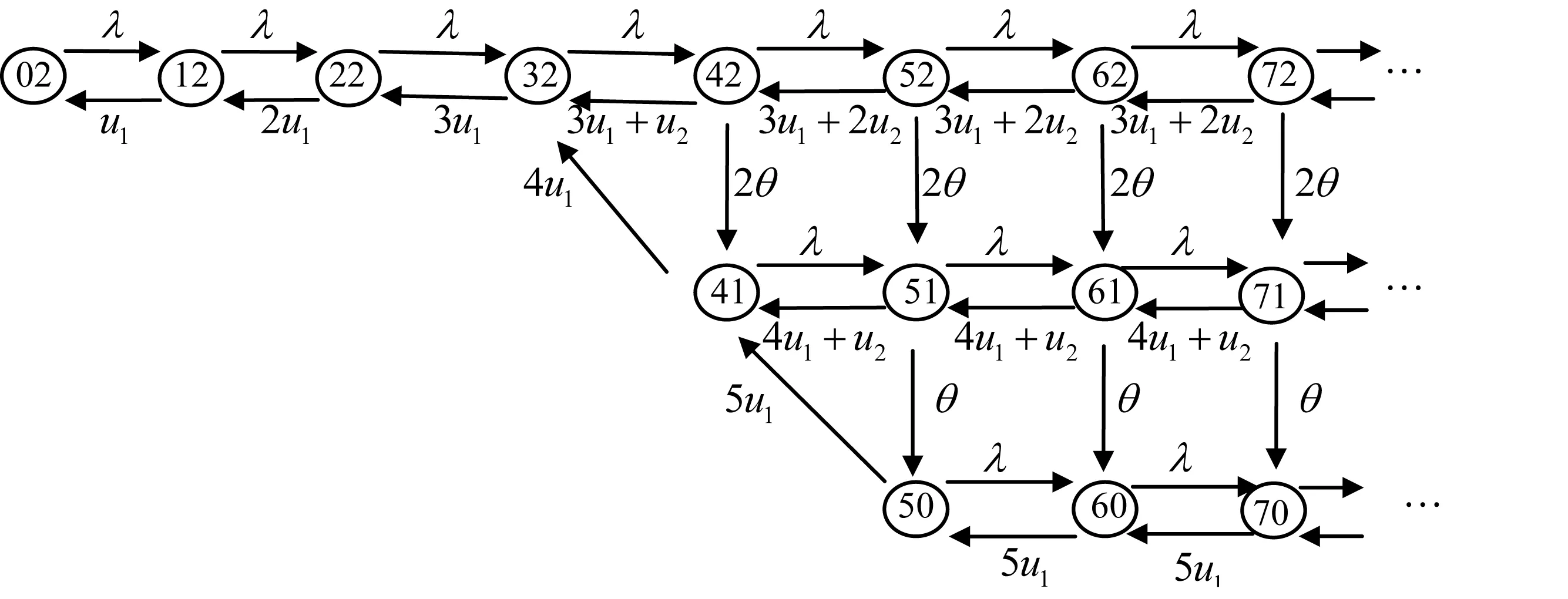
1.2 率阵R

1.3 系统的稳态性指标
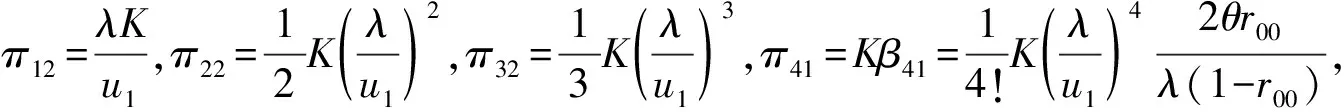

1.4 条件随机分解结果
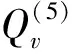

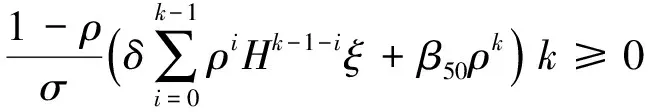





2 结束语
——国外课堂互动等待时间研究的现状与启示

