区间复模糊软集的距离测度及其应用

范建平，成 瑞，吴美琴

山西大学 经济与管理学院，太原030006

1 引言

为了适应系统的日益复杂性，更精确地描述并表示信息，Zadeh[1]于1965 年提出了模糊集理论，而后得到广泛关注。越来越多的学者对模糊理论进行了扩展，例如直觉模糊[2]、区间模糊集[3]、Vague 集[4]、区间直觉模糊集[5]、犹豫模糊集[6]、双犹豫模糊集[7]、Pythagorean 模糊集[8]、中智集[9]等。其中区间模糊集理论由Turksen[3]于1986 年提出，是对模糊集理论最为重要的拓展，其用隶属度上界和隶属度下界两个属性来描述模糊信息，比原有的模糊集理论更具有灵活性。

在某些情况下，上述模糊理论无法对研究对象进行分类，有学者开始考虑软集[10]理论。Maji等人[11]将软集理论与模糊集理论相结合，提出了模糊软集概念。随后有直觉模糊软集[12]、区间模糊软集[13]、区间直觉模糊软集[14]、Vague 软集[15]、犹豫模糊软集[16]、双犹豫模糊软集[17]、Pythagorean 模糊软集[18]、中智软集[19]等概念的提出。

上述模糊软集理论被广泛应用，但是它们只能处理数据的不确定性，但是无法处理某段时间内数据的波动性，生活中，可以经常看到随着时间的推移周期性变化的数据。为了解决适应这种情况，Ramot 等人[20]提出了复模糊集的概念，添加了描述信息周期性变动的相位项，复模糊集的隶属度取值不限于[0，1]，而是扩展到复平面中的单位圆，从而将隶属度由实数扩展到复数。Alkouri 和Salleh[21]将复模糊集概念扩展到复直觉模糊集。Greenfield 等人[22-23]提出了区间复模糊集概念并随后给出了区间复模糊集的相关运算。Selvachandran 等人[24]将区间复模糊集应用于马来西亚经济中。

随后，上述理论逐渐发展，Selvachandran 等人[25]将复模糊集、软集、Vague 集结合提出了复Vague 软集及其距离测度。随后，Selvachandran 等人[26]给出复Vague 软集的关系。Selvachandran 等人[27]提出了区间复模糊软集的概念。

在距离测度方面，Wang和Xin[28]提出了直觉模糊集的相似测度和距离测度。Zhang[29]提出了直觉模糊集和区间直觉模糊集的新距离测度方法。Yang和Hussain[30]基于Hausdorff 测度开发了犹豫模糊集的距离和相似性测度，并将这些测度应用于多准则决策和聚类分析。Singh[31]提出了双犹豫模糊情况下基于距离和相似性测度的多属性决策。Zeng 等人[32]提出了Pythagorean 模糊集和Pythagorean 模糊数的不同距离测度。Muharrem[33]为区间直觉模糊集开发了一种新的距离测度方法，并将其应用于具有不完全权重信息的群决策问题。Khalid和Abbas[34]提出了直觉模糊软集和区间直觉模糊软集的距离测度和运算。Peng 和Yang[35]提出了区间模糊软集的信息测度。Wang 和Qu[36]提出了模糊软集的熵，相似性测度和距离测度。

由Yoon 和Hwang[37]定义的TOPSIS 算法是一种被广泛使用的算法。TOPSIS 法通过最大化正理想解距离和最小化负理想解距离的决策规则来选择最佳目标。Chen[38]将TOPSIS 应用于模糊环境。Ashtiani 等人[39]提出了基于区间模糊集的TOPSIS算法。Kumar和Garg[40]在区间直觉模糊环境下提出了基于集对分析的TOPSIS算法。Peng 和Yang[41]提出了一种基于最大化偏差法和区间犹豫模糊软集的TOPSIS 的算法。Sun 等人[42]提出了基于犹豫模糊相关系数的TOPSIS算法并给出了相关应用。Tan 和Zhi[43]提出了直觉犹豫模糊集环境下的TOPSIS算法。

在现有文献中，没有关于区间复模糊软集距离测度的研究，并且没有基于区间复模糊软集的距离测度的TOPSIS 算法。因此，本文研究了区间复模糊软集的距离测度，以及区间复模糊软集的加法、乘法、部分隶属度和部分非隶属度的运算。本文还研究了区间复模糊软集的距离测度的运算性质，并给出了证明。此外，提出了基于区间复模糊软集距离测度的TOPSIS 算法。最后，将这种算法应用于经济分析中。

2 相关概念

定义1[3]给定论域U，A是U 上的区间值模糊集，定义为：

定义2[13]F( )

U 为给定论域U 上的幂集，E 为参数集且A ⊂E，F 是F:A →F(U )的映射，( F,A) 是U 上的区间模糊软集，定义为：

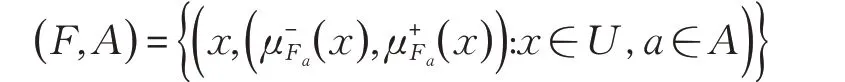
定义3[22]给定论域U，A是U 上的区间复模糊集，定义为：

定义4[27]给定论域U，E为参数集且A ⊂E，F(U )为给定论域U 上的幂集，F 是F:A →F(U )的映射，( F,A)为U 上的区间复模糊软集，定义为：

定义5[27]对于任意两个区间复模糊软集( F,A )和( G,B)，基本运算定义如下：

（1）对于任意x ∈U 满足下列 条件，则(F,A )⊆( G,B)：

定义6[27]区间复模糊软集( )

F,A 的补集定义为：( F,A)C=( FC,A)=

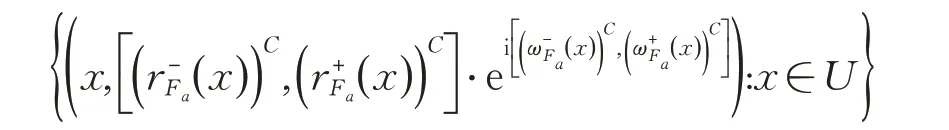
定义7[27]区间复模糊软集( F,A )和( G,B )的交运算（并运算）得到的集合为区间复模糊软集( H,C)，定义为：

其中，对于任意a ∈A,b ∈B,x ∈U 且C=A ⋃B。

定理1[27]区间复模糊软集( F,A),( G,B),( H,C )的运算定义为：

（1）( F,A )∨( G,B)=( G,B )∨( F,A)

（2）( F,A )∧( G,B)=( G,B )∧( F,A)

（3）( ( F, A) ∨( G,B ))∨( H,C )=( F,A) ∨(( G,B )∨ ( H ,C))

（4）( ( F, A) ∧( G,B ))∧( H,C )=( F,A) ∧( ( G, B )∧( H,C))

定理2[27]对于任意两个区间复模糊软集( F,A),( G,B )满足De Morgan定律：

（1）( ( F, A) ∨( G,B))C=( F,A)C∧( G,B)C

（2）( ( F, A) ∧( G,B))C=( F,A)C∨( G,B)C

3 区间复模糊软集的运算性质和距离测度

3.1 区间复模糊软集的运算性质

定义8 区间复模糊软集( F,A )和( G,B )之间的加法，乘法，部分隶属度，部分非隶属度的运算定义如下：

定 理3 给定区间复模糊软集( F,A)，2( F,A)=( F,A )⊕( F,A),3( F,A)=( F,A) ⊕( F,A )⊕( F,A) …可得：

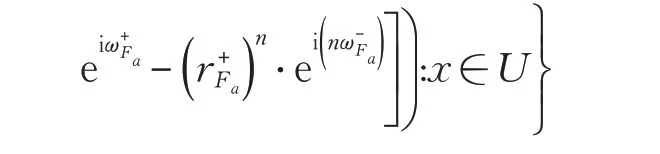
定理4 给定区间复模糊 软集( F,A) ，( F,A)2=( F,A )⊗( F,A),( F,A)3=( F,A) ⊗( F,A) ⊗( F,A )…可得：

3.2 区间复模糊软集的距离测度

定义9 对于任意两个区间复模糊软集( F,E),( G,E)之间的距离测度应当满足下列性质：

（1）0 ≤ |d( ( F, E),( G,E ))|≤1。

（2）d( ( F, E),( G,E ))=0 ⇔( F,E )=( G,E)。

（3）d( ( F, E),( G,E ))=1 ⇔对 于∀ei∈E,xj∈U，满足下列条件：

情形1

情形2

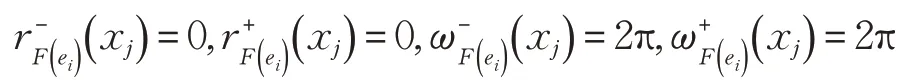
情形3

且

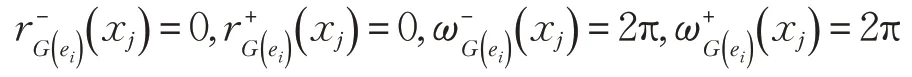
情形4

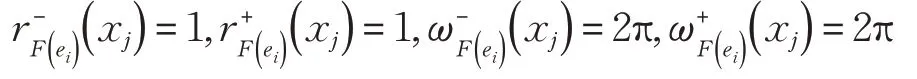
（4）d( ( F, E),( G,E ))=d( ( G, E),( F,E))

（5）( H, E )∈IV-CFSS(U ),若( F,E )⊆( G,E )⊆( H, E), 则d( ( F, E),( H, E ))≥max(d( ( F, E),( G,E )),d( ( G, E),( H, E)))

定理5 定义10 中的距离测度是区间复模糊软集之间的有效距离测度。

证明若定义10 中的区间复模糊软集Hausdorff 距离测度是有效距离测度，它需要满足定义9 中的性质（1）～（5）。 考 虑 两 个 区 间 复 模 糊 软 集( F,E )={F( ei)|i=1 ,2 ,… ,m },( G,E )={G (ei)|i=1,2,… ,m}则：

（1）因为

可得：

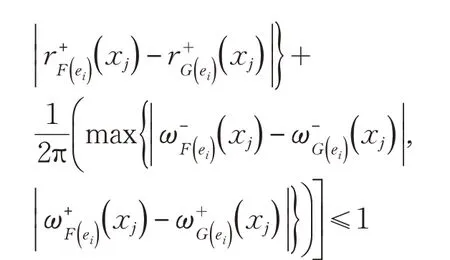
所以0 ≤ |d1( ( F, E),( G,E ))|≤1。

情形1

情形2

情形3

情形4

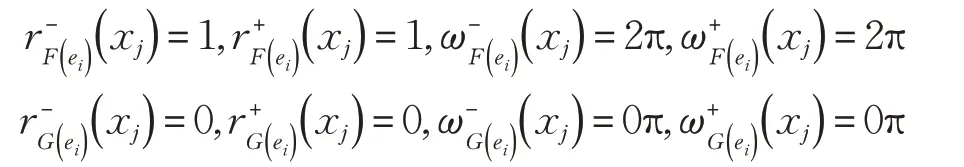
（5）若( F,E )⊆( G,E )⊆( H,E),则

因此

所以，d1( ( F, E),( H,E ))≥d1( ( F, E),( G,E))

同理可得，d1( ( F, E),( H,E ))≥d1( ( G, E),( H,E))

所以，d1( ( F, E),( H, E ))≥max(d1( ( F, E),( G,E )),d1( ( G, E),( H,E)))

证毕。

区间复模糊软集Euclidean 距离测度和区间复模糊软集Hamming距离测度的证明同上。

定义11 对以上三种距离测度进行拓展可以得到广义区间复模糊软集Hausdorff 距离测度、广义区间复模糊软集Euclidean距离测度：

同区间复模糊软集Hausdorff 距离测度的证明相同，以上区间复模糊软集距离测度为有效距离测度。

当λ=1时，广义区间复模糊软集Hausdorff 距离测度退化为区间复模糊软集Hausdorff 距离测度，广义区间复模糊软集Euclidean 距离测度退化为区间复模糊软集Hamming 距离测度；当λ=2时广义区间复模糊软集Euclidean 距离测度退化为区间复模糊软集Euclidean 距离测度。

定 义12 假 设ei∈E 的 权重 为wi，wi∈[0,1 ],i=1,2, … ,m，则可以得到广义区间复模糊软集加权Hausdorff 距离测度、广义区间复模糊软集加权Eu‐clidean距离测度：

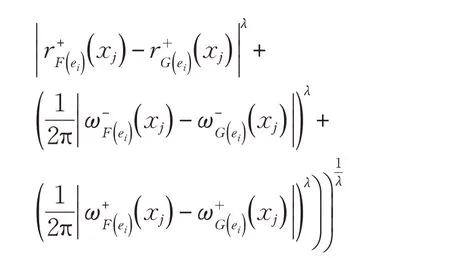
定义13 当定义12 中广义区间复模糊软集加权Hausdorff 距离测度和广义区间复模糊软集加权Euclid‐ean距离测度中λ=1时，得到区间复模糊软集加权Haus‐dorff 距离测度和区间复模糊软集加权Hamming 距离测度：

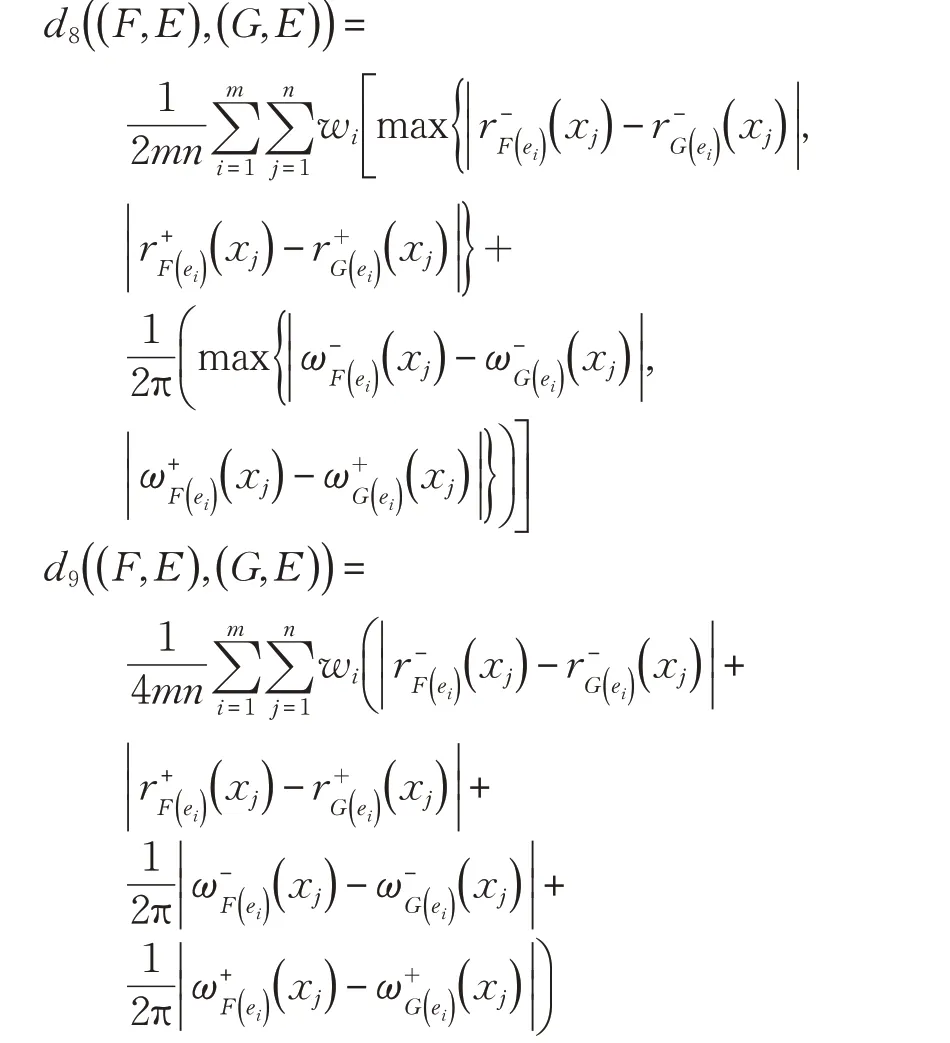
证明省略。

定义14 当定义12 中广义区间复模糊软集加权Euclidean 距离测度中λ=2时，广义区间复模糊软集加权Euclidean 距离测度退化为区间复模糊软集加权Euclidean距离测度：

证明省略。

3.3 距离测度的运算性质

本文提出了多种区间复模糊的距离测度公式，下面定理只给出区间复模糊软集Hausdorff 距离测度的证明，其他测度证明类似。

定理6(U ,E )上的区间复模糊软集：

（1）若( F,E )=∅,则d( ( F, E),( F,E)C)=1

（2）若( F,E )=1,则d( ( F, E),( F,E)C)=1

（3）若( F,E )=( F,E)C,则d( ( F, E),( F,E)C)=0

证 明（1）若 ( )F,E =∅，则 对于任 意，那么：

所以对于区间复模糊软集Hausdorff距离测度：

（2）性质（2）的证明同性质（1）的相同。

（3）性质（3）显然成立，证明省略。

定理7 区间复模糊软集之间的距离测度满足下列性质：

（1）d( ( F, E),( G,E)C)=d( ( F, E)C,( G,E))

（2）d( ( F, E),( G,E ))=d( ( F, E )∧( G,E),( F,E )∨( G,E))

（3）d( ( F, E),( F,E )∧( G,E ))=d( ( G, E),( F,E )∨( G,E))

（4）d( ( F, E),( F,E )∨( G,E ))=d( ( G, E),( G,E )∧( G,E))

证明

（2）性质（2）显然成立，证明省略。

（3）根据定义7可得：

那么

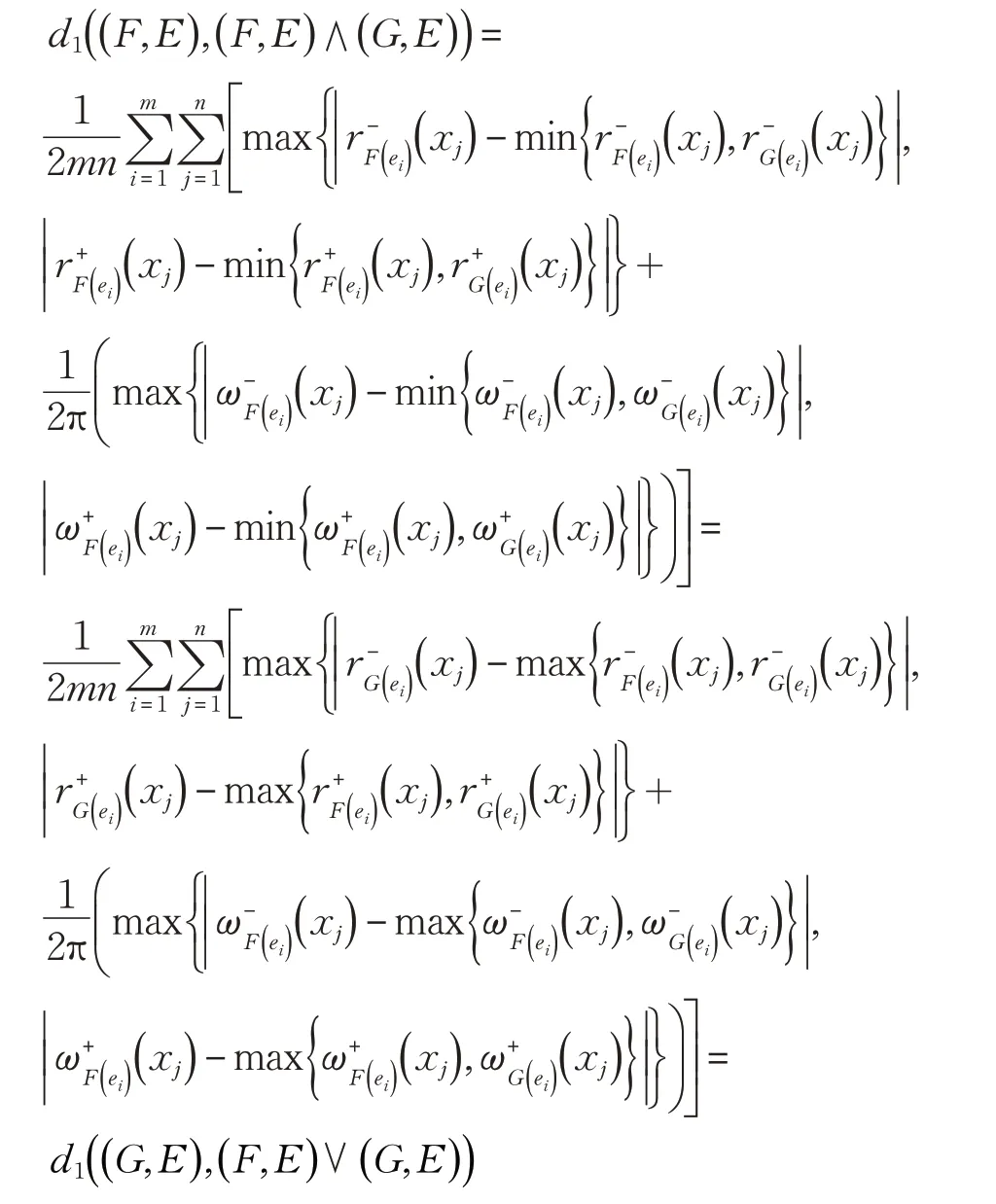
（4）性质（4）的证明同性质（3）相同。

定理8 区间复模糊软集之间的距离测度满足下列性质：

证明根据定义8可得：

所以

证毕。

同理，对于上述定义的其他区间复模糊软集的距离测度，上述定理仍然成立，所以d( ( G, E),( F,E )⊕( G,E ))。

定理9( F,E )为区间复模糊软集，可得：

证明因为

则

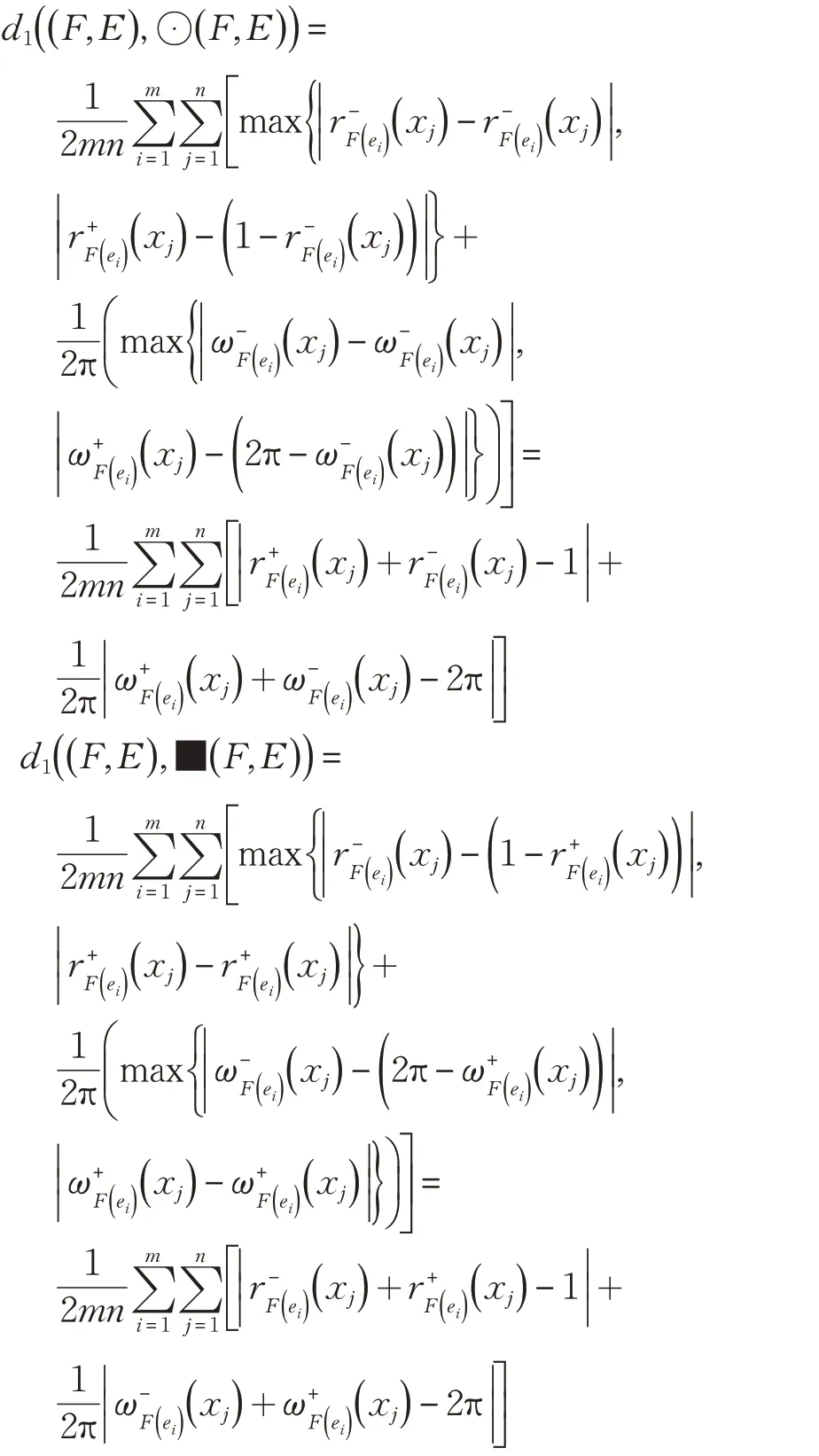
同理，在上述所定义的其他区间复模糊软集的距离

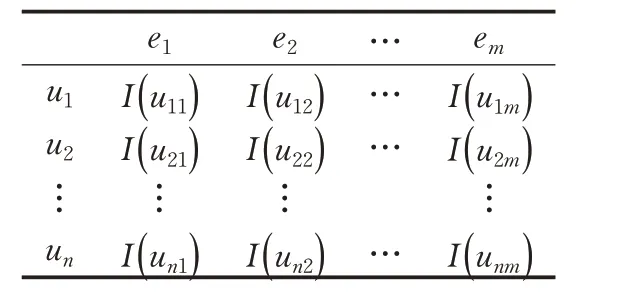
表1 区间复模糊软集( F,E)

4 基于区间复模糊软集距离测度的TOPSIS算法

步骤1 构建区间复模糊软集的决策矩阵，其表示所有的决策信息，如表1所示。

步骤2 基于最大偏差法，通过以下公式确定属性权重wi,i=1,2,… ,m：

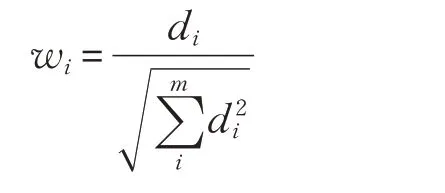
其中，di定义为区间复模糊软集Euclidean 距离测度：

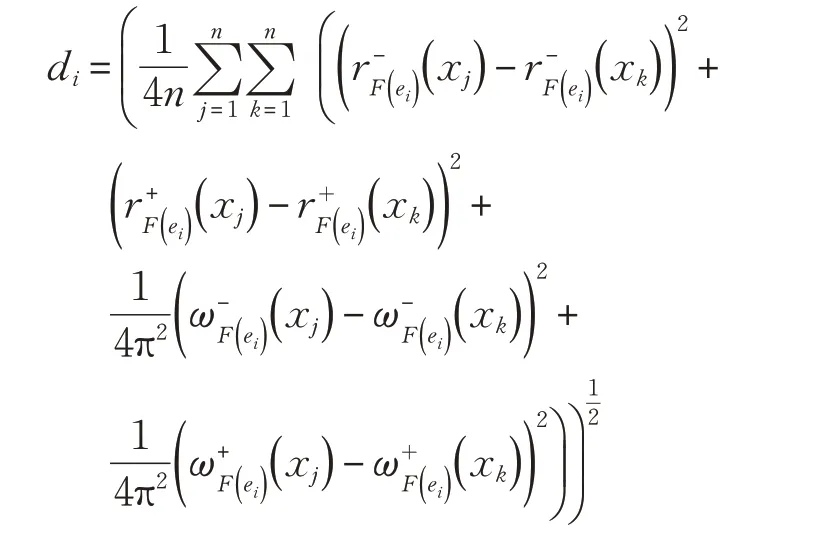
然后将wi标准化，得到：

步骤3 确定正理想解I+=( I1+,I2+, …,Im+)和负理想 解 I-=( I1-,I2-…, ,Im-)，其 中 Ii+( i= 1,2, …,m )是{ I( u1i),I( u2i),… ,I( uni)}中的正理想值，对成本型指标为最小值，对效益型指标为最大值。Ii-( i= 1,2,… ,m )是{ I( u1i),I( u2i), …,I( uni)}中的负理想值，对成本型指标为最大值，对效益型指标为最小值。

步骤4 本文定义计算区间复模糊软集Ij与正理想解I+=( I1+,I2+,… ,Im+)和 负 理想 解I-=( I1-,I2-,… ,Im-)的加权Euclidean距离d10( Ij,I+)和d10( Ij,I-)：

步骤5 通过下列公式计算与正理想解的贴近度：

其中，0 ≤Cj≤1,j=1,2, ,n。

步骤6 根据计算所得的贴近度，对方案进行降序排列，确定最理想目标。

5 算例

第4 章中给出的算法可以对国家经济政策对省份的影响作用进行排序。本章给出一个经济分析算例来说明第4章中所提出的算法的可行性。

表2 区间复模糊软集形式的M国经济政策对省份的影响信息

假设U={u1=A省,u2=B省,u3=C省,u4=D省,u5= E 省 }，表 示 M 国 的5 个 省 份 集 合，E={e1=政策A,e2=政 策 B,e3=政策C} 表示M 国的政策的参数集，本文运用区间复模糊数来表示经济政策对某一省份的影响程度。现在，要对M国的经济政策对于哪个省份影响最大，且产生作用周期最短进行排序，选择综合影响最大的省份。

步骤2 根据第4 章给出的公式计算属性权重得w1=0.23,w2=0.22,w3=0.54。

表3 和

表3 和

d10( Ij,I-)d10( Ij,I+)u11.485 21.722 0 u21.833 71.833 7 u33.462 60.646 4 u42.598 71.304 3 u51.256 82.800 3

表4 计算所得贴近度

表5 区间模糊软集形式的M国经济政策对省份的影响信息

步骤4 计算Ij与正理想解与负理 想 解的 加 权Euclidean 距 离d10( Ij,I+)和d10( Ij,I-)的结果如表3所示。

步骤5 计算贴近度，并对贴近度进行降序排列，如表4 所示，得到u5≻u1≻u2≻u4≻u3，所以M 国的综合经济政策对E省影响最突出。

由于区间复模糊软集为提出的新概念，在区间复模糊软集环境下，目前还没有与本文方法类似的多属性决策方法的研究。所以本文将邹斌等人[44]提出的基于区间模糊软集的多属性决策方法与本文提出的基于区间复模糊软集的TOPSIS多属性决策方法进行比较。将上述经济分析中的区间复模糊软集形式的数据转化为区间模糊软集形式，保留幅度项，舍去相位项，转化后的数据在表5 中给出。根据文献给出的决策方法，得到排序结果：u3≻u1≻u5≻u2≻u4。

显然，本文提出的方法的排序结果与邹斌等人[44]提出的方法的排序结果不同。最大不同在于经济政策对于E 省综合影响的排序，在本文提出的决策方法中经济政策对于E 省的综合影响排最后，而邹斌等人[44]提出的方法经济政策对于E 省的综合影响排第一。导致这种完全相反的排序结果的原因在于给定的数据舍弃了可以反映经济政策对经济影响的时间滞后的描述，即相位项，而经济政策对于E 省的影响的时间滞后明显短于其他省份，所以得到了相反的排序结果。不难发现，本文给定的决策方法对于数据的描述更为全面、客观，可以得到更为合理的排序结果。

6 结论

本文定义了区间复模糊软集之间的多种距离测度，包括Hausdorff 距离、Hamming 距离、Euclidean 距离、广义Hausdorff 距离、广义Euclidean 距离、广义加权Haus‐dorff 距离、广义加权Euclidean 距离、加权Hausdorff 距离、加权Hamming距离、加权Euclidean距离。并提出了区间复模糊软集的加法、乘法、部分隶属度和部分非隶属度运算以及区间复模糊软集距离测度的相关性质。此外，提出了一种基于区间复模糊软集距离测度的TOPSIS 算法。最后，通过算例说明了该算法在经济分析中的应用。本文还存在一些不足之处，如给定数据存在一定主观随机性。在以后的研究中，重点研究复模糊软集在其他模糊集中的推广和应用。