基于视觉感知的图像放大

杜宏伟，乔美丽，宋 刚，张云峰，包芳勋

1.山东财经大学 计算机科学与技术学院，济南250014

2.山东省数字媒体技术重点实验室，济南250014

3.山东省教育招生考试院，济南250011

4.山东大学 数学学院，济南250100

1 引言

图像放大是指由低分辨率（Low Resolution，LR）图像通过插值获得高分辨率（High Resolution，HR）图像的一种图像处理技术[1]。从信号角度来说，插值是一个离散采样点与插值核函数卷积的过程，如果一个信号是带限信号，则此信号可以完全由采样信号利用理想滤波器sinc 函数重建[2]，但是sinc 函数只能通过近似来实现。早期的插值算法如最近邻插值、双线性插值、双三次插值[3]和三次样条插值[4]等都是近似sinc 函数，它们相对简单且易于实现，但重建后的图像会出现不同程度的锯齿和模糊现象。

为此，学者们做了更深入的研究。一般来说，插值算法大致可分为离散方法和连续方法两类。离散方法是指利用已知像素点通过某种变换确定未知像素点。文献[5]提出一种新的边缘指导的图像插值方法（New Edge-Directed Interpolation，NEDI），该算法根据LR 与HR协方差系数的几何对偶性计算出插值函数中的权重系数，从而求出未知点的像素值。文献[6]提出一种基于多方向滤波和数据融合的图像插值方法（an edgeguided image interpolation algorithm via Directional Filtering and Data Fusion，DFDF），将每个待插点的邻域分成两个观测子集，并从正交的两个方向估计待插点的灰度值。文献[7]提出了一种基于软决策的图像插值方法，其参数和数值估计采用最小二乘法。文献[8]提出一种边缘指导图像插值方法，利用泰勒级数展开的近似方法，对于待插像素点沿其四个方向估计像素值。基于非局部几何相似性和方向梯度，文献[9]对周围像素点加权平均确定插值点像素值，根据正则化最小二乘法确定权重系数。以上这些算法能较好地保持插值图像的空间相关性，且具有良好的主观视觉质量和图像客观质量评价值。但是，这些图像插值算法主要基于离散思想，不能够对图像进行任意倍数的放大，而且与传统的方法相比，时间复杂度相对较高。虽然这些插值算法能够把图像边缘部分处理地较好，但是在细节部分会出现走样、噪声等现象。

连续方法是指将图像离散采样数据转换为连续的灰度曲面，然后确定未知像素点。文献[10]提出了一种基于分段常张力基样条的插值方法，与传统的三次样条方法相比，它可以有效避免图像出现振铃现象。文献[11]使用图像数据作为约束构造拟合曲面来还原采样过程。基于构造的有理插值函数，文献[12-15]提出的插值模型能够很好地刻画图像的结构，可以在插值数据不变的前提下通过调整参数获得更好的图像质量，此类方法能够有效保留图像的细节信息。

近年来，深度学习作为人工智能方面的一个重要分支，得到人们的广泛关注。目前基于学习的方法主要分为两类：一类是基于图像自身的学习，一类是利用图像外部信息的学习。前者根据图像的自相似性进行图像重建。将稀疏编码与深度学习方法相结合，文献[16]提出了一种基于深度卷积神经网络的图像超分辨重建算法（Cascaded Sparse Coding Network，CSCN）。此算法利用图像自身的相似冗余信息，避免了图像出现人工痕迹，但若LR中没有足够的冗余信息，此类算法会导致细节丢失。后者借助附加的图像库的信息进行图像重建。文献[17]通过端到端的方式学习LR 图像与HR 图像之间的映射关系，提出了一种基于全卷积神经网络的超分辨率算法（Super-Resolution Convolutional Neural Network，SRCNN），提高了重建效果。然而，该算法的重建效果取决于的训练的图像库，且训练时间较长。

图像插值实际上是一个主客观（人眼视觉感知和图像）相统一的过程。根据人眼视觉感知特性，人眼更关注于图像的边缘区域而非平滑区域。文献[18]提出了一种基于人眼对比敏感度的图像增强算法，通过单一参数对图像局部梯度的调节来增强局部图像对比度。将对比度增强视为最优化问题，通过感知约束最大化图像的平均局部对比度，文献[19]提出了一类新的人类视觉系统（Human Visual System，HVS）指导的以神经网络为技术支撑的自适应插值方法。根据HVS 的特征建立了一个模糊决策系统，把输入图像的像素分为人眼感知敏感类和非敏感类，不同的区域使用不同的插值手段。但此方法的局限性在于图像像素的划分方法与所用的插值方法不一致，这样可能导致图像内在的自然属性（非线性、多尺度特性、方向性）遭到破坏。在插值过程中，如果把人眼视觉特性、图像区域划分、图像插值等融合在一个模型中，最大化保护图像自然属性，具有重要的理论意义。

本文把图像插值与人眼视觉感知相结合，提出了一种自适应视觉感知的图像放大方法。根据图像结构，构造一类新的含有可调参数的有理函数插值模型，当形状参数都取1 时，此有理插值模型退化为多项式插值模型。该模型通过调节形状参数，可以获得最佳的插值曲面。基于本文构造的模型进行图像插值，首先利用等值线方法将输入图像自适应地划分为边缘区域和非边缘（平滑）区域。然后，在图像结构简单且人眼关注度低的平滑区域，采用多项式模型插值；在图像结构复杂且人眼关注度高的边缘区域，采用有理模型插值，其形状参数根据人眼视觉感知特性进行自适应调节。最后，获得高质量的插值图像。

2 插值模型

2.1 双变量有理插值函数

令f(x,y)为平面区域Ω:[a,b;c,d]上的双变量有理插值 函 数，{(xi,yj,fi,j),i=1,2, …, n, n+1j;=1,2,… ,m,m+1}为Ω 上给定数据点集，fi,j=f(xi,yj)。对xy 平面上任何点 (x,y)∈[xi,xi+1;yj,yj+1]，hi=xi+1-xi，θ=(x-xi)/hi，lj=yj+1-yj，η=y-yj/lj，对每个y=yj,j=1,2,… ,m+1，构造x方向的插值曲线：

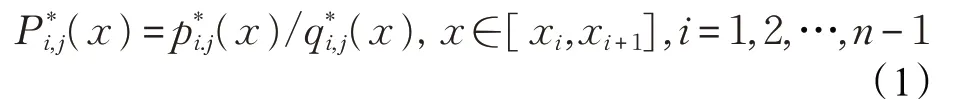
其中αi,j＞0，且

在节点x1和xn处，偏导数定义为：

对每个点对(i,j);i=1,2, …,n-1和j=1,2, ,m-1，使用x 方向的插值函数(x)来定义上的有理插值函数Pi,j(x,y)如下：

其中

该插值函数由插值数据和形状参数确定，形状参数取值不同，表达形式也不相同，特别地，当αi,j=βi,j=1时，该模型退化为多项式插值模型。

图像可视为二维平面上的等距节点数据。给定一幅m×n的图像Im,n，fi,j(0 ≤i ≤m-1,0 ≤j ≤n-1)是Im,n内坐标为(i,j)的像素值，目的是得到图1 中红色像素点所在面片的数学表达式，从而确定图像中的任一点fi,j的像素值。

图1 有理插值模型

如图1 所示，根据公式（5）定义的插值函数Pi,j(x,y)，给 定12 个 像 素 点 fi,j-1，fi+1,j-1，fi-1,j，fi,j，fi+1,j，fi+2,j，，fi,j+1，fi+1,j+1，fi+2,j+1，fi,j+2，fi+1,j+2，可以构造一个过4个像素点fi,j,fi+1,j,fi,j+1,fi+1,j+1的矩形面片。

2.2 插值函数的性质

性质1 设Pi,j(x,y)为定义在[xi,xi+1;yj,yj+1]上的有理插值函数，对于任意的正参数αi,j和βi,j，则

定理1 设为等距节点，即hi=(b-a)/n。若参数 βi,j满 足 βi,j=βi+1,j,i=1,2,… ,n-2，则 插 值 函 数Pi,j(x,y)在插值区间[x1,xn;y1,yn]上C2连续。

公式（5）定义的插值模型含有形状参数，插值曲面的形状可以通过形状参数来调节。但性质1 给出了曲面的有界性质，即无论参数如何调整，曲面的变化都被约束在边界内。考虑到图像灰度值[0，255]的限制，所以在调整曲面的过程中，曲面要同时满足边界约束和灰度范围限制。与C1连续的有理插值函数相比，本文构造的C2连续有理插值函数在插值面片的内部和拼接处光滑性更好，可有效保持插值图像清晰的边缘结构。

2.3 人眼视觉感知特性

人眼对于空间不同对比度的敏感度符合韦伯定理。韦伯定理是指感觉的差别阈限与标准的刺激强度之比是一个常数。令C 为局部对比度增强阈值，∂C 表示对比度感知变化，超出差别阈值，则∂C 和C 满足：

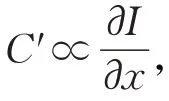
基于韦伯定理，通过自适应调整公式（5）中的参数α,β 来改变曲面的梯度。插值区域的平均梯度表示为δ，若插值区域像素变化剧烈，δ就越大，意味着图像梯度变化也越大。面片梯度grad( Pij( x,y ))表示为：

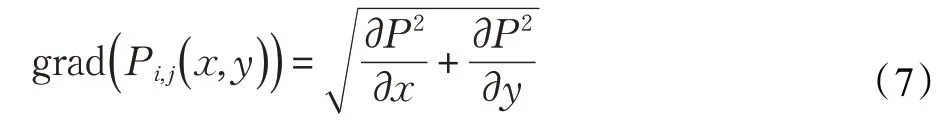
由以上公式可知，曲面的拉伸程度与曲面的梯度成正相关非线性关系。人类的视觉适应具有S 型非线性特点，通常用Sigmoid 函数来刻画[20]。Sigmoid 函数模型如下

其中，ϑ 为最大值和最小值的差值，μx为S函数在x轴上的偏移，k 表示边缘的倾斜程度，μy为S函数在y 轴上的偏移。如图2 所示，Sigmoid 函数满足人眼视觉特性且具有非线性[21]，用它来表示δ与grad(Pi,j(x,y))的非线性、正相关关系。

图2 Sigmoid型函数模型

3 本文算法

用等值线方法对图像进行边缘检测，检测出来的平滑区域结构相对简单，采用多项式模型插值；边缘区域结构复杂，基于人眼对比敏感度准则对公式（5）自适应调整αi,j和βi,j。

3.1 自适应区域划分

目前，经典的边缘检测方法如Roberts算子、Laplace算子等可以利用图像梯度将图像的边缘检测出来。但是，Roberts 算子对图像边缘附近的区域内产生较宽的响应，不能有效检测到图像的高频细节，处理后图像缺失细节信息；Laplace 算子对孤立像素的响应比对边缘或线的响应更强烈，所以处理后图像会产生很多孤立点。以上检测方法的结果不能很好地反映图像的自然属性。本文根据构造的插值模型来选择边缘检测方法，实现了图像划分与图像插值的有机统一，最大化保护图像的自然属性。

根据等值线绘制原理，对每个插值单元绘制等值线。插值单元指图1 中由[ ]i:i+1;j:j+1 围成的矩形（即红色像素点围成的矩形）。存在等值线的插值单元为边缘区域，否则为平滑区域。区域检测的阈值应能概括描述该插值单元的灰度信息，且信息相关性最大，所以选取插值单元上的4个像素点及其四邻域点共12个像素点的均值作为自适应区域检测的阈值，即自适应检测阈值为：

令Δxm,n=fm,n-λ,m,n=0,1，根据等值线绘制原理，若Δxm,n是同号，则此插值单元属于平滑区域，反之属于边缘区域。因此，可以利用等值线方法对图像进行区域划分。如图3 所示，若在一个插值单元中四个顶角符号不同，则该插值单元属于边缘区域。图3（a）中Δxm,n表示一个插值单元中对应的四个顶点。（b）～（e）表示在一个插值单元中四个顶点的符号不同时的边界检测结果。图4 为图像边缘检测结果。其中，（a）是原图像，（b）～（d）分别是图像用等值线方法、Laplace算子和Roberts算子的边缘检测结果。可以看出，等值线方法可以有效地检测到图像的纹理和边界。

图3 基于正负号的纹理检测

图4 图像边缘检测结果

3.2 图像插值

对于平滑区域，采用多项式插值模型。对于边缘区域，采用有理插值模型，形状参数根据人眼视觉敏感度自适应设置。

当α 和β 都等于1 时，公式（5）就变成了多项式插值，表达式如下：

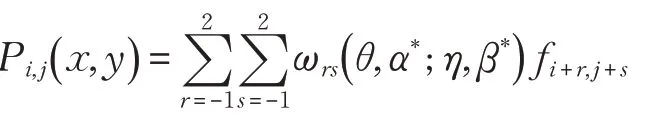
图5 图像插值示意图

单元周围12 个像素点构造出该插值单元的曲面，确定插值点的灰度值，右图为图像插值后的示意图。

3.3 基于人眼视觉感知的参数自适应调节

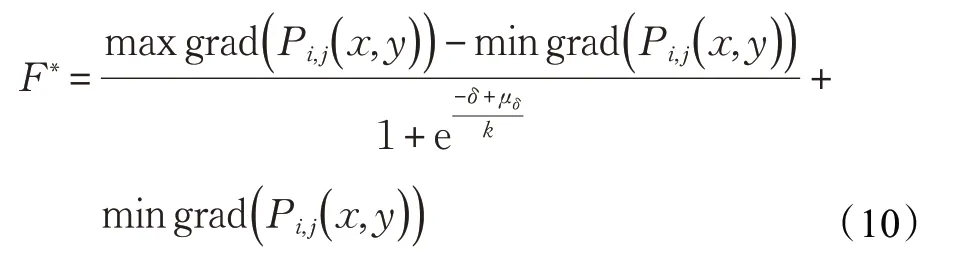
其中，k 代表此S 型函数的陡峭程度，μδ代表S 型函数向δ 轴 正 方 向 移 动 的 距 离，max grad( Pi,j( x,y ))和min grad( Pi,j( x,y ))分别表示梯度的最大值和最小值。在2×2 的面片上，数值计算每一个像素点的梯度值，由此确定对应最大、最小梯度值所在像素点的曲面坐标，将相应坐标代入插值函数，即可得到max grad( Pi,j( x,y ))、min grad( Pi,j( x,y ))。此时，F∗是一个关于α、β 的二次函数，其值是S型函数在梯度最大时的函数值。由曲面的有界性可知，一张面片的插值函数在闭区域上梯度有界。最后，根据F∗的值确定α∗、β∗的取值。2×2面片上四个像素点梯度的数值计算公式为：

其中，G(r,s),r=i,i+1,s=j,j+1为像素点在(r,s)处的梯度值。

若在点( x∗,y∗)处Pi,j( x,y )取得最大值Pi,j∗( x,y)，且要 重 新 定 义 为 ：

图像的信息熵反映了图像包含的信息量，图像的信息熵越大，图像的对比度就越高，图像的视觉效果就越好，从表1 中可以看出，基于人眼视觉感知对形状参数调节后，图像的信息熵变大，图像的视觉效果提高。

4 实验

实验选取9 幅标准测试图像，如图6 所示。采用隔行隔列下采样，选取具有代表性的算法bicubic、NEDI[5]、DFDF[6]、RSAI[7]、SRCNN[17]、CBI[22]、DCCI[23]、A+[24]与 本文算法进行比较。下面主要从主、客观效果和时间复杂度3个方面来测试本文算法的效果。

表2 给出了不同插值算法的客观评价数据：峰值信噪比（Peak Signal To Noise Ratio，PSNR）和结构相似性（Structural Similarity Index，SSIM）。从表1 可以看出，与其他方法相比，本文提出的方法拥有最高平均PSNR和SSIM值，具有较强的竞争力。

表1 形状参数自适应调节后图像信息熵值比较

图6 标准测试图像

图7 ～图11 提供了各插值算法的视觉效果比较，并将局部细节放大显示。其中，图7 和图8 突出显示了不同算法对图像边缘区域的重建效果，图9、图10 和图11展示了对图像纹理细节区域的刻画效果。如图7 所示，由bicubic、A+、SRCNN 重建的图像出现了严重的锯齿现象，RSAI、ICBI、DCCI和DFDF方法出现了模糊、锯齿现象，本文算法和NEDI有效保持了图像边缘的光滑性。如图8 所示，bicubic 出现了边缘模糊现象，NEDI 算法出现了斑点噪声，RSAI、A+和SRCNN 算法产生了不连续的条纹，ICBI 也出现了边缘失真现象，其余各算法保持了清晰的边缘。在处理图像纹理细节方面，如图9 所示，NEDI、RSAI、ICBI、DCCI 都出现了严重的扭曲变形、纹理错乱现象，DFDF 算法也丢失了图像细节信息，A+和SRCNN 出现了纹理变形、噪声现象，不能有效保持图像的结构特征，本文方法有效地保持了图像的结构特征。从图10 可以看出，本文算法较好地恢复了图像的细节，其余算法出现了不同程度的细节扭曲现象。图11 是Barbara 图像的局部细节展示（图6 红框标注的部分），从对桌布、桌腿等细节的重建效果来看，本文算法的视觉效果最好。因此，从图像细节的刻画效果来看，本文算法优于其他算法。

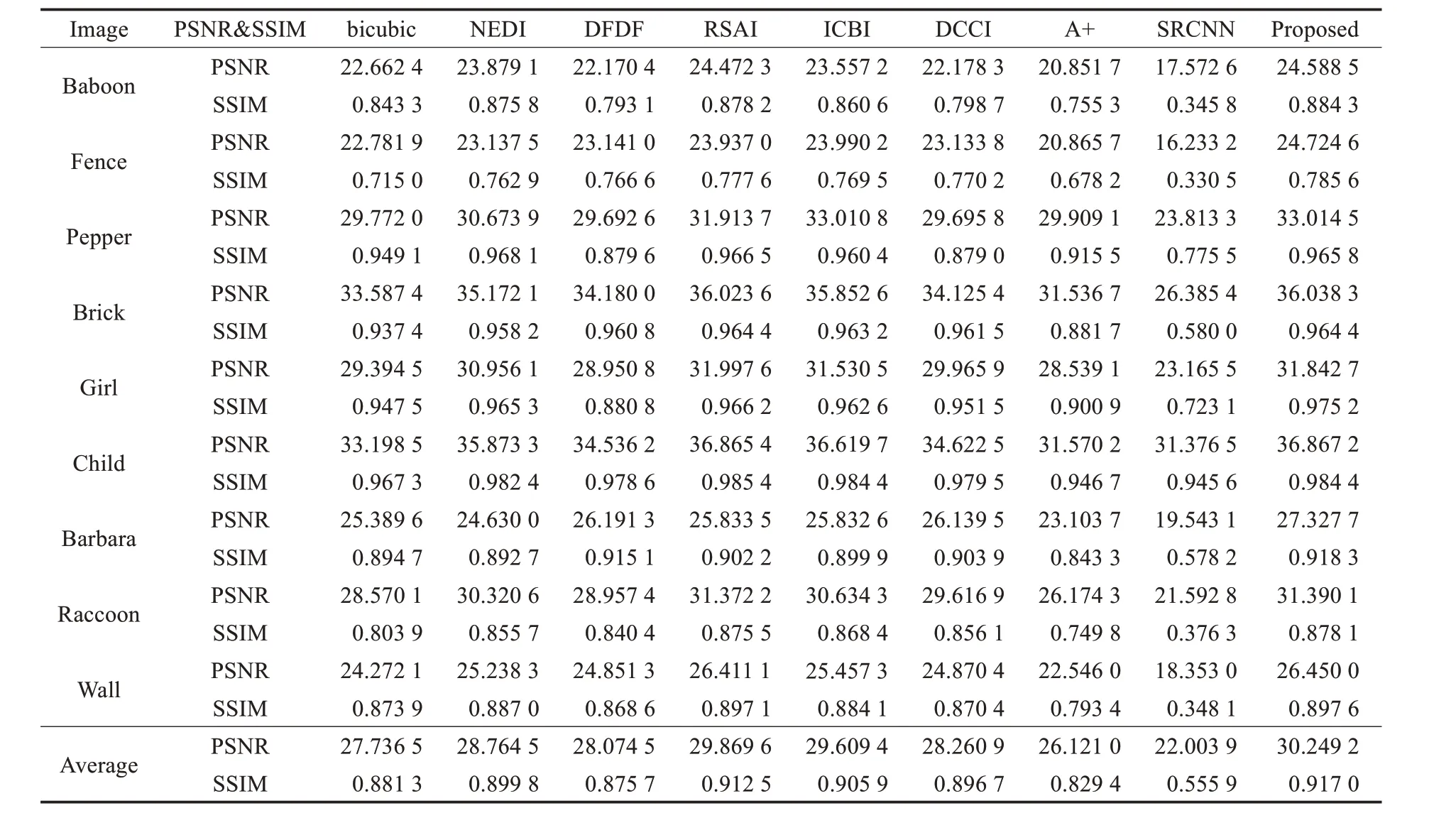
表2 不同方法的PSNR和SSIM值比较

图7 不同算法Girl对比图

图8 不同算法Fence对比图

图9 不同算法Wall对比图

图10 不同算法Raccoon对比图

在实际的应用中，不仅要求获得好的图像质量，同时，图像的处理速度也是非常重要的。从理论上分析，本文方法对一个插值面片进行插值包括自适应区域划分，构造插值模型，形状参数确定，它们都是简单的代数运算，时间复杂度是O(1)。对于一个m×n大小的图像，插值面片有(m-3)×(n-3)个，整幅图像遍历一遍时间复杂度是O(m×n-3m-3n+9)，所以本文算法总的时间复杂度是3×O(1)×O(m×n-3m-3n+9)≈O(m。×n)上述分析可以看出，本文算法的时间复杂度与多项式插值算法处于同一量级。如表3 所示，本文算法在保证图像质量的情况下，拥有较低的运行时间。

图11 不同算法Barbara对比图

表3 不同插值算法运行时间对比s

基于以上分析，bicubic总体上插值效果不及其他插值算法，尤其在图像的边缘区域。NEDI 算法是基于边缘指导的插值算法，此方法可以保持图像清晰的边缘结构，而在处理纹理细节较多的区域时，会导致纹理扭曲、变形或产生噪点。DFDF 算法不会使图像的纹理细节扭曲变形，但是视觉效果不理想，尤其在图像的非边缘区域容易出现细节信息丢失现象。RSAI算法在一定程度上保持了图像的细节信息，而在图像的边缘区域容易产生锯齿现象。ICBI 算法可以获得较高的客观评价数据，但在图像的纹理细节区域容易出现扭曲变形现象。DCCI 算法对图像边缘区域的重建效果较为理想，在图像的纹理细节区域也容易出现扭曲变形现象。A+和SRCNN 算法的重建效果依赖于训练图像库，当测试图像与训练图像不属于同一类图像库时，容易产生纹理失真，边缘锯齿现象。相对于上述算法，在视觉效果上，本文算法保持了图像原有的结构信息，在客观数据方面，PSNR提高了0.37～8.24 dB，且时间复杂度较低。

5 结束语

基于构造的双变量有理函数插值模型，本文提出了一种自适应视觉感知的图像放大算法。利用人眼视觉感知规律，对插值函数的形状参数进行适应性调节，实现最优插值。根据等值线绘制原理，提出等值线方法来检测图像的边缘信息，基于构造的插值模型选取边缘检测的阈值，将区域划分与图像插值融合在一个模型里，最大化保护图像的自然属性。因构造的插值模型具有简单的显性表达式，本文算法具有较低的时间复杂度。实验证明本文算法取得较好的主客观效果。