面向提升旅客出行效率的高速铁路列车停站方案优化

许若曦，聂 磊，付慧伶*

(1.北京宇恒未来规划设计有限公司，北京100022；2.北京交通大学交通运输学院，北京100044)

0 引言

我国高速铁路运营里程长，很多长距离列车的平均停站次数较多，增加了旅客(特别是长途旅客)的旅行时间；同时中小站的列车服务频率偏低，换乘旅客的等待时间也较长.这些问题可以通过优化列车停站方案解决，即减少部分列车的中小站停站次数，提高快车比例；并适当增加中小站的列车停站频率，确保中小站旅客获得足够的站间通达性和换乘便捷性.由于互为矛盾，如何平衡好这两者间的关系，是列车停站方案优化面临的一个问题.

对于列车停站优化问题，国内外有丰富的研究成果.Yu-Hern Chang[1]，Dung-Ying Lin[2]，Y.Ulusoy[3]针对台湾和北美铁路列车停站进行优化，以铁路和旅客出行的成本最低为目标；蒲松[4]基于客流需求波动建立列车开行方案鲁棒优化模型，可决策列车OD、开行对数和停站方案；牛丰[5]构建不确定客流条件下的高速列车停站方案机会约束规划模型，最小化区段内开行列车的总停站次数；J.Qi[6]同时优化列车开行区段、停站和客流分配，最小化列车空载席位和总停站次数；史峰[7]基于旅客时变需求优化高速列车开行方案，并设计停站方案确定方法；毕明凯[8]基于随机客流优化市郊铁路的停站方案，最小化列车总运行时间.

针对长距离高铁，既有研究在优化列车停站方案时，较少关注同时提升不同等级车站之间和不同出行距离旅客的出行效率.本文提出“减少部分列车的停站次数以提高大站间快车比例，同时增加相邻大站间站站停列车以保障中小站列车服务频率”的列车停站优化措施，兼顾大站旅客快速直达，中小站旅客直达与换乘相结合的多种需求，减少旅客总出行时间损失.

1 问题描述与建模

1.1 高速铁路列车停站方案优化问题

本文立足提升我国高速铁路旅客出行效率，旅客出行效率损失通过列车停站产生的旅客等待时间，以及旅客换乘的等待时间损失来衡量.结合现状列车停站方案(作为初始方案)，通过减少部分列车的中小站停站次数，提高大站间快车比例、吸引大站客流；同时增加相邻大站间站站停列车，确保中小站与邻近大站之间有足够的通达性和换乘便捷性.优化过程中，根据现状客流分布，将受停站调整影响的客流重新分配到其他列车上.问题的优化目标为最小化所有旅客的时间损失.

对研究对象做出如下假设：①不调整初始方案中列车的起讫点、频率和径路；②初始方案中的列车带流情况已知，由客票数据得出，仅对因取消停站不能被原列车服务的客流进行重新分配；③考虑旅客出行便捷性，规定旅客出行至多换乘1次；④列车停站时间设置为常数，旅客换乘时间假设为合理范围内的均值；⑤优化方案可能因列车旅行时间缩短而吸引更多旅客，也可能因中小站列车停站次数减少，部分旅客流失；假设短期内的客流量固定，暂不考虑客流诱增及流失情况.

1.2 优化模型

模型中使用的符号含义如表1所示.

列车停站优化模型为

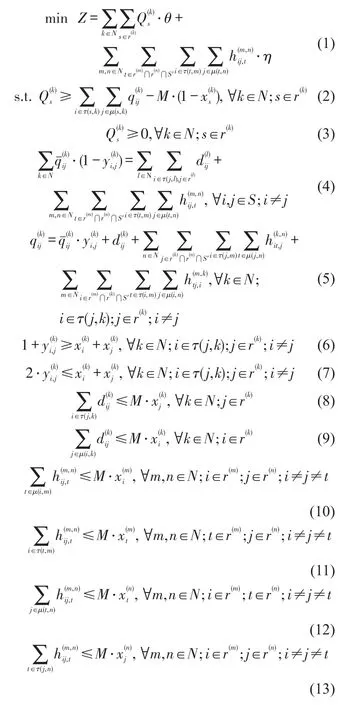
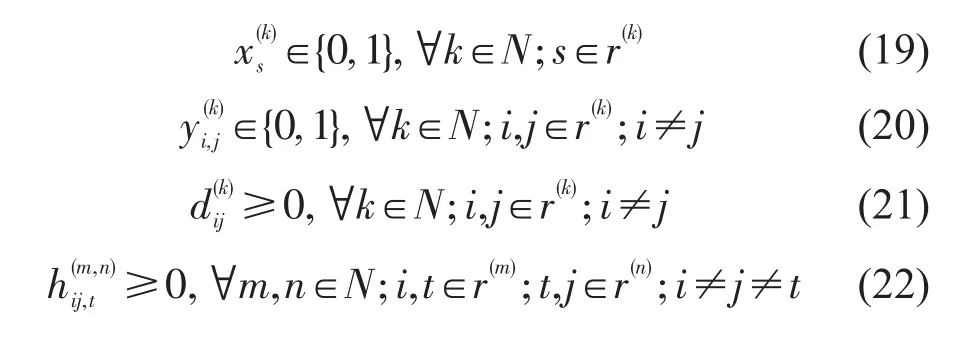
表1 模型符号说明Table 1 Notations of model

目标函数：式(1)最小化所有旅客的时间损失，第1项表示列车中途停站给列车上旅客带来的停站等待时间，第2项表示旅客由于换乘增加的等待时间.约束条件：式(2)和式(3)为目标函数线性化约束，作用是避免目标函数非线性化.式(4)～式(7)为客流守恒约束，当取消列车的某个停站时，与该停站相关的旅客既可以转移到其他直达列车，也可以转移到另外两趟列车换乘出行；转移客流量等于直达转移与换乘转移的客流之和，列车两个停站之间的客流量等于原客流量与直达、换乘转移来的客流量之和；其中，式(6)和式(7)为变量耦合约束.式(8)和式(9)为直达旅客上下车约束，当且仅当都等于1时，大于0，即列车能够服务车站i与j之间的旅客.式(10)～式(13)为旅客选择列车m、n换乘出行约束，当且仅当都等于1时，大于0，即列车能够服务车站i与j之间并在t站换乘的旅客.式(14)～式(17)为列车停站约束，其中，式(14)为列车k在经过的所有大站都必停(该约束也可以被松弛)；式(15)和式(16)表示列车k在其起讫点站必停；式(17)表示列车k在运行径路上未经过的车站不能停站.式(18)表示某列车经过的任一区段，列车上的客流量不能大于该列车定员.式(19)～式(22)限制决策变量取值范围.

2 遗传算法设计

上述模型为混合整数线性规划.当实例规模较大时，模型变量会急剧增加，直接求解难度很大.为提高求解效率，结合问题特点设计如下遗传算法，流程如图1所示.

图1 遗传算法求解流程Fig.1 Solving process of genetic algorithm

(1)编码及初始化.

染色体按路网车站和列车直接编码，将所有列车头尾相连编为一行，形成染色体，每列列车编码位数相同，为路网中车站个数.例如，给定5个车站和4趟列车的停站方案，对列车停站方案的染色体编码方式如图2所示，其中，1表示停站，0表示不停站.从图2可知，染色体长度为20位(4×5=20)，每条染色体为所有列车的一种停站组合.

图2 染色体编码形式Fig.2 Coding form of chromosome

将现状列车停站方案和列车带流情况作为初始解，利用邻域搜索法生成限定规模的初始种群.以图2染色体I为例，生成步骤如下：

Step 1将染色体随机分成n个基因片段，确定每个基因片段的基准点，如图3所示，n=3.

Step 2确定该点左右两边各m个点作为该基准点的邻域，图3中m=2.

Step 3通过随机数控制各邻域内的点是否发生改变，遍历邻域内每个点时生成0～1之间的随机数.若随机数小于等于0.5，则发生改变；否则，不改变.

Step 4改变n、m取值及基准点位置，Step 1～Step 3操作，得到更多种群个体.

(2)解的可行化修复.

求解模型时直接调用Gurobi对转移客流进行重新分配，保证不违背客流守恒、旅客上下车、变量取值等约束.故在遗传算法求解过程中，主要存在新个体违背列车定员及停站约束的问题.

对于违背列车停站约束的个体，强制转换列车停站状态，使其满足式(14)～式(17).对于违背列车定员约束的个体：一种可行化方法为放弃该染色体，继续搜索其他可行方案；另一种方法为适当调低遗传参数变异概率取值，防止某一车站多数列车的停站被取消，降低不可行解出现的概率.

图3 邻域搜索法生成初始种群Fig.3 Generation of original population using neighborhood search method

(3)适应度评估.

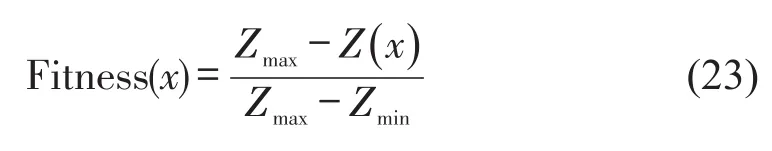
式中：Fitness(x)为种群中个体x的适应度值；Zmax为初始种群中目标函数值最大的个体的目标函数值；Zmin为预估的目标函数值下界；Z(x)为每代种群中个体x的目标函数值.式(23)为选取的适应度函数.

迭代过程中，若个体x1目标函数值Z(x1)大于Zmax，将该个体舍弃；若个体x2目标函数值Z(x2)小于Zmin，令Zmin=Z(x2)，重新计算当代种群中各个体的适应度值.

(4)遗传操作.

实例中，选择操作采用轮盘赌方式，交叉操作选择多点交叉算子，变异操作采用基本位变异法.

3 实例分析

选取京广高铁作为实例研究对象，总里程2 298 km，共36个车站，本文对下行方向(北京至广州)的列车停站方案进行优化.

3.1 数据准备

案例基于某年度11月某平峰日(周三)09:00-12:00时段内的列车运行图及客流数据，共有本线与跨线列车42列(跨线列车及其客流被预处理为本线区段列车和客流).车站按下行方向顺序编号为1～36.列车停站时间损失θ=7 min(含起停车附加时分)，旅客换乘等待时间损失η=60 min，各列车定员按运行图中列车的实际定员取值.

遗传参数(种群规模、迭代次数、变异概率)取值对求解结果有较大影响.本文通过测试大量遗传参数组合，平衡考虑求解效率与解的质量，确定种群规模取10，迭代次数取100，变异概率取0.015.

3.2 模型求解

考虑是否松弛模型约束式(14)，以及是否增加相邻大站间站站停列车，设计3个不同的列车停站调整方案，如表2所示，以便于进行方案优化效果的对比.表中“相邻大站间站站停列车”不是由算法产生的，是根据列车的起讫点设置条件与合理运距范围预先指定的列车.

表2 列车停站调整方案Table 2 Strategies of adjusting train stops

应用Python 2.7与Gurobi 7.5执行遗传算法，计算机配置为Intel(R)Core(TM)i7-6500U CPU(2.60 GHz)、8.00 GB.基于表2中的3个方案，对应求解得到3个列车停站方案；限于篇幅仅展示方案3，如图4所示，其寻优收敛过程如图5所示.各方案指标如表3所示.

图4 优化的列车停站方案(方案3)Fig.4 Optimized train stop plan(plan 3)

图5 方案3寻优收敛过程Fig.5 Convergence of plan 3 in process of optimization

3.3 优化结果分析

与初始方案相比，3个优化方案的列车总停站次数减少，分别为258，230，247次(初始方案为323次)；旅客时间损失较初始方案均显著降低.方案3在增加相邻大站间站站停列车(图4中的“L”列车)后，与方案1相比，目标函数值进一步优化，比初始方案旅客时间损失减少了40.08%.由于不限制列车在大站必停，方案2的优化幅度最大，比初始方案旅客时间损失减少40.14%.

由于减少列车停站次数，约30%客流需转移至其他列车.但换乘客流量并未增加很多(表3)，约占总客流的1%～4%；其中，方案3增加的站站停列车使中小站旅客换乘出行更便捷，所产生的换乘客流最多.

定义“大站间快车”为除大站外，在中小站总停站次数不超过设定数值σ的列车(如北京至广州σ≤6的列车为大站间快车，σ取值与列车运距正相关)，以此统计优化方案的大站间快车数.与初始方案相比，方案1和方案3中的“大站间快车”数分别增加70.9%和94.4%，大站之间的旅客有更多快车可以选择.其中，方案3的列车停站时间损失最少，因此大站间快车数的增幅最高.

从模型目标函数值来看，方案2的优化程度最高，但大站列车服务频率被降低.方案3保证列车在大站都停站的基础上，与方案2的目标函数值相近；虽然换乘客流较多，但每3 h开行1列相邻大站间站站停列车，增加了中小站的列车停站频率，不仅提升了车站之间的通达性，也可以较大程度地缩短旅客的换乘等待时间.

综合上述分析，列车停站方案3具有较好的优化效果.

表 3 列车停站方案优化结果指标Table 3 Indicators of optimized train stop plans

4 结论

为提升我国长距离高速铁路旅客的出行效率，本文基于减少列车中小站停站次数，增加相邻大站间站站停列车策略，建立以最小化旅客时间损失为目标的列车停站方案优化混合整数规划模型，并设计了遗传算法.

在京广高铁实例研究中，通过对比3个不同的优化方案结果，验证了“增加相邻大站间站站停列车”策略最有助于减少长距离列车的停站次数，节省的列车停站时间最多且远超出换乘时间的增加，使旅客出行效率指标较实际方案得到了明显提升：增加大站间快车数，增幅达到94.4%，从旅行时间方面增强了高铁竞争力；由于每3 h在相邻大站之间增加开行站站停列车，中小站列车频率至少为1列/(3h)，有助于引导部分旅客便捷换乘出行；旅客总体时间损失减少40.08%.

下一步研究可同时优化列车起讫点、开行频率和停站，进一步提高列车开行方案质量；并通过铺画列车运行图验证方案的可实施性.