基于改进Copula的海上运输关键节点应急保障能力评估

李宝德，吕 靖，李 晶

(大连海事大学交通运输工程学院，辽宁大连116026)

0 引言

海上运输关键节点是指船舶在海上航行时经过的特殊地理位置的海上区域，主要包括海峡、运河等[1].海上运输关键节点应急保障能力是指在其所属区域发生突发险情时，海上运输关键节点能够实施应急处置的能力，故应急保障能力强弱对于损失的轻重具有重要影响.

针对海上应急的研究主要围绕海上应急资源调配、船舶应急等，较少对具体海上运输关键节点应急保障能力进行研究.AI等[2]研究了海上应急资源的选址分配问题，提出一种将选址和分配相结合的离散非线性整数规划模型.YANG等[3]对海上船舶应急能力评价模型进行了研究.朱乐群[4]就海上通道应急决策问题，提出一种两阶段相似度匹配的应急方案选择方法.高天航[5]基于两阶段DEA模型分析了海上通道关键节点的应急效率.

Copula函数由Sklar提出之后，在二十世纪九十年代得到迅速发展[6].随着Copula函数理论的不断成熟，利用Copula函数适用于边缘分布为任意形式的优越性构建联合分布函数，在多领域广泛应用于描述多种随机变量间的相关研究[7].在海运领域研究不是很多，王爽[8]采用Vine Copula对原油海运网络中节点连通可靠性进行了分析.当随机变量的维数增加时，Copula函数参数求解难度也随之增加.因此，一些学者采用降维的思想将多元随机变量转化为少数几个相互独立的变量，运用到Copula函数中，降低了Copula函数参数求解难度[9].

鉴于已有研究，本文以海上运输关键节点为视角，充分考虑影响海上运输关键节点应急保障能力的多种影响因素间的关联性及因素分布情况，利用构建的FA-Copula函数模型对主要的运输关键节点应急保障能力进行评估，该方法降低了Copula函数的参数求解难度，本文结果为相关部门的海上应急决策提供了依据.

1 应急保障能力评估指标体系构建

1.1 应急保障能力影响因素

海上运输关键节点突发事件应急保障一方面与可以实施的保障力量有关，另一方面与这些保障力量能否实施所受到的影响有关.

针对海上运输关键节点突发事件应急救援的主要部门是所属相关应急保障机构，如我国的海上搜救中心，美国的海岸警卫队等，是影响海上运输关键节点应急保障的主要方面；除了专门应急保障机构外，也有利益国之间的合作共同应对海上突发事故，如我国与美国签署的《中美海上搜救协定》，与朝鲜签署的《中朝海上搜救协定》等，共同实施相关区域的应急保障.另外，事故周围航行的船舶如果能第一时间实施救援，对提高应急保障能力具有重要的影响.

相关的法律协定是国际间合作的基础，针对海上应急国际海事部门也出台了一些法律法规，如《国际救助公约》《国际海上搜寻救助公约》等.此外，面对国际政局的不稳定，一些海上运输关键节点会出现被封锁的可能，故海上运输关键节点所属国政局稳定性也会影响相关应急机构的应急保障能力.

1.2 评估指标体系构建

根据指标体系建立原则，结合运输关键节点应急保障能力影响因素，建立评估指标体系，如表1所示.

表 1 海上运输关键节点应急保障能力评估指标体系Table 1 Evaluation index system of emergency guarantee capability of key nodes in maritime transportation

2 应急保障能力评估的FA-Copula模型构建

依据Copula理论，将一个联合分布函数分解为Copula函数和边缘分布函数的乘积来描述变量之间的依赖关系[10].因子分析充分考虑影响因素的相关性，利用降维思想将具有错综复杂关系的影响因素表示成对变量起解释作用的少数公共因子[11].运用因子分析，提取相互独立的公共因子，结合Copula函数构建联合分布，计算海上运输关键节点应急保障能力.

2.1 应急保障能力影响因素因子分析

2.1.1 标准化处理

原始数据量纲不同，使用标准化公式进行处理.

正向指标为

逆向指标为

2.1.2 因子分析

计算相关性矩阵R并进行KMO与Bartlett球形检验；然后计算累计方差贡献率及因子载荷，确定选取的因子，以及因子与各个因素之间的关系表达式.

式中：为公共因子得分；Fij为第i列第j个公共因子，共有n行m列；X为原始数据矩阵；R-1为相关矩阵的逆矩阵；B为旋转后的因子载荷矩阵.

2.2 应急保障能力评估的Copula函数模型构建

根据Sklar定理[6]，海上运输关键节点应急保障能力影响因素的Copula函数为

式中：F(x1,x2,…,xm)为m维影响因素变量的联合分布函数；m为变量个数；C为Copula函数；θ为Copula函数的参数 ；u1=F1(x1),u2=F2(x2),…,um=Fm(xm)为影响因素变量X1,X2,…,Xm的边缘分布函数.

基于对影响因素变量进行的因子分析，得到q个相互独立的公共因子，结合式(4)，海上运输关键节点应急保障能力评估的Copula函数为

式中：u1,u2,…,uq为得到的海上运输关键节点应急保障能力影响因素公共因子的边缘分布函数.

2.3 公共因子边缘分布函数确定

常用的分布线型有正态分布、Gamma分布、指数分布、对数分布、广义极值分布(GEV)等.FISHER[12]对GEV进行理论研究，提出了3种极值分布，其标准化分布函数为

式中：ε为形状参数；μ为位置参数；σ为尺度参数.ε=0为极值Ι型，又称Gumbel分布；ε＞0为极值 ΙΙ型，又称Frechet分布；ε＜0 为极值 ΙΙΙ型，又称Weibull分布.

以Kolmogorov-Smirnov(K-S)检验方法检验公用因子边缘分布的拟合效果，比较均方根误差(RMSE)的值ERMSE和信息准则(AIC)的值LAIC的大小优选边缘分布，边缘分布优选原则为ERMSE及LAIC越小拟合效果越好[13].

式中：dri为第r个公共因子对应第i个关键节点的理论频率值与经验频率值之差，经验频率值通过Gringorten[14]公式计算，即

式中：Ps表示大于或等于影响因素指标xs的经验频率值；s为计算得到的每个公共因子值从大到小排位的项数；α根据Gringorten取值为0.44.

式中：η为所选分布线型中参数的个数.

3 实例分析

3.1 研究对象选取及数据来源

根据之前的研究[1]，结合全球航线所经过的海上运输节点事故发生情况，筛选14个重要的海峡及运河进行实例研究分析，具体如图1所示，图中白点为发生的事故.

本文数据是针对各个关键节点隶属区域目前所设立的相关应急机构、保障性机构，签署的国际合作应急协议、制定及加入的应急公约进行统计得到的，主要来源于各个国家相关网站、国际海事组织网站、相关文献等；船舶流量是根据www.shipxy.com进行统计得到的.另外，数据选取的时间段是2010年1月1日～2018年12月31日.

图1 2018年海上事故分布图Fig.1 Distribution map of maritime accidents in 2018

3.2 计算结果及分析

3.2.1 因子分析结果

利用SPSS 22对标准化后的应急保障能力影响因素数据进行因子分析，计算得到KMO值为0.776，Bartlett检验值小于0.05，适合做因子分析.根据特征值大于1，提取3个累计方差贡献率达到83.926%的公共因子，如表2所示.具体因子载荷矩阵，公共因子与各影响因素之间的关系如表2和表3所示.

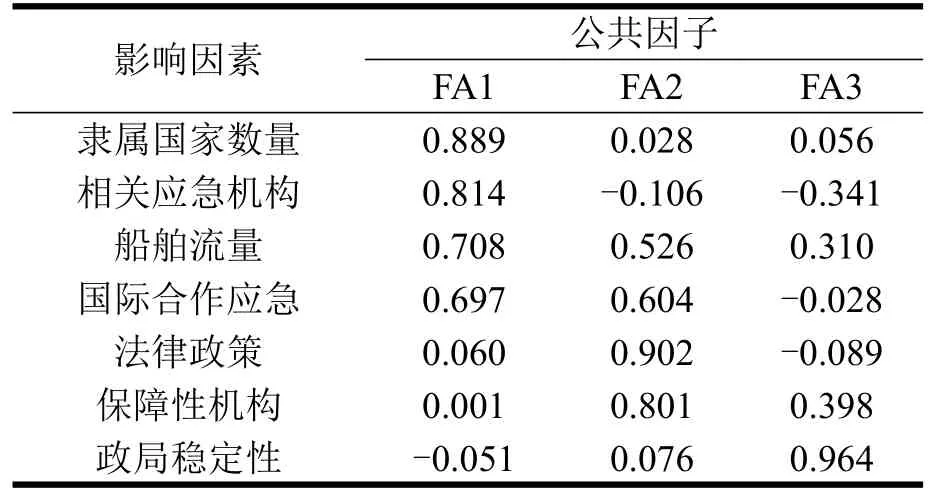
表2 旋转因子载荷矩阵Table 2 Rotation factor load matrix

从表2中可以看出，FA1在船舶流量、国际合作应急、隶属国家数量和法律政策4个因素的因子载荷较高，可以利用FA1来解释上述4个因素对海上运输关键节点应急保障能力的影响；同理，利用FA2来代表相关应急机构和保障性机构两个因素，利用FA3代表政局稳定性.

表3 公共因子得分系数Table 3 Score coefficient of common factors

表3中各个公共因子与影响因素关系式可以进行各个关键节点的应急能力计算，但缺乏考虑各个影响因素分布特征，Copula函数能够根据各公共因子的分布特征建立联合分布，且不受各单因子变量边缘分布的影响.

3.2.2 优选各个公共因子边缘分布

根据常见的分布线型分别对提取的3个公共因子进行分布拟合，并进行K-S检验，通过检验的各个公共因子边缘分布结果及对应的ERMSE和LAIC如表4所示.

从表4可以看出：FA1通过检验的分布为正态分布和Frechet分布，进一步比较ERMSE和LAIC，Frechet分布的ERMSE和LAIC最小，故FA1优选Frechet分布；基于Frechet分布FA2的ERMSE和LAIC也最小，故FA2也优选Frechet分布；FA3通过检验的分布为正态分布和Weibull分布，比较ERMSE和LAIC发现Weibull分布的ERMSE和LAIC最小，故FA3优选Weibull分布.

表 4 各个公共因子分布线型拟合效果Table 4 Distribution fitting results of common factors

3.2.3 海上运输关键节点应急保障能力评估

根据优选的公共因子分布并结合式(5)，关键节点应急保障能力评估值表述为

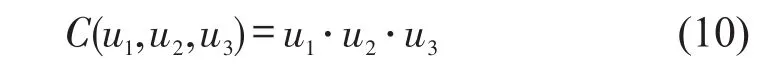
式中：u1,u2,u3分别表示公共因子FA1，FA2，FA3优选的边缘分布函数，值越大说明应急能力越强.

根据式(10)得到的关键节点应急保障能力如表5所示，3个公共因子影响计算结果如表6所示.

表 5 海上运输关键节点应急保障能力评估结果Table 5 Evaluation results of emergency guarantee capability of key nodes in maritime transport

从表5可以看出：14个关键节点应急保障能力综合对比较高的是直布罗陀海峡、马六甲海峡和巴拿马运河，较低的是苏伊士运河；重要的石油运输通道霍尔木兹海峡应急保障能力相对靠前；对于马六甲海峡可替代通道的巽他海峡和龙目海峡应急保障能力相对较弱.

表 6 公共因子的应急影响评估值Table 6 Emergency impact evaluation value of common factors

从表6可以看出：FA1对应急保障能力影响较大的是马六甲海峡，较小的是苏伊士运河；FA2影响比较大的是苏伊士运河，较小的是弗罗里达海峡；FA3影响比较大的是巴拿马运河，较小是龙目海峡.所以目前针对海上运输各个关键节点的应急保障侧重有所不同.

从图2和图3中看出：FA1分布应急保障能力值最大的是马六甲海峡，FA1和FA3联合分布应急保障能力值最大的朝鲜海峡；FA2分布和FA2与FA3联合分布也会出现类似情况，说明不同公共因子的联合分布与单个因子的分布对评估结果的变化影响是不同的.所以，要充分考虑各个影响因素的边缘分布及其联合分布情况，使评估结果更具可靠性.

图2 FA1及其联合分布比较图Fig.2 Comparison chart of FA1 and its joint distribution

图3 FA2及其联合分布比较图Fig.3 Comparison chart of FA2 and its joint distribution

4 结论

本文以海上运输关键节点为视角，考虑影响关键节点应急保障能力因素的相关性、分布情况及多维变量导致Copula函数求解困难的问题，基于构建的FA-Copula模型对14个重要海峡及运河的应急保障能力进行评估.结果表明，综合对比应急保障能力比较好的是直布罗陀海峡，比较差的是苏伊士运河.通过比较提取的公共因子及其联合分布的应急能力值变化情况，说明不同因子边缘分布的影响是不同的，评估时要充分考虑各个影响因素的分布情况.此方法为海上应急保障能力评估提供了新思路，结果为相关部门的应急决策提供了参考.

本文评估的是现存的应急保障能力，而这些保障能力机制的形成是管理者需要思考及下一步需要研究的.