基于复杂网络的中国出口集装箱运价指数波动规律

汤 霞，匡海波，郭媛媛，蓝贤钢

(1.大连海事大学综合交通运输协同创新中心，辽宁大连116026；2.珠海城市职业技术学院经济管理学院，广东珠海519000)

0 引言

运价变化是航运市场波动最直观的表现，受航运市场供需变化、世界经济、政治因素等多方面因素影响.中国出口集装箱运价指数(CCFI)自1998年发布以来，客观反映了集装箱班轮运输市场波动状况.准确把握CCFI波动规律，可为航运市场主体运营决策，以及政府政策制定提供一定的参考.

关于CCFI波动的研究，主要集中于CCFI波动特征及影响因素.研究发现，CCFI波动具有持续性、非对称性、集聚性、周期性等特征[1-2]，CCFI波动的影响因素主要包括船舶运力、货运需求、季节因素、宏观经济、重大事件影响等[2-3].研究方法主要采用计量经济学、人工智能、组合模型等，如ARCH、GARCH、AR-GARCH、模糊时间序列模型、EMDHT组合模型等[1-4].

现有研究取得了一定成果，但仍存在以下不足：一是，主要从运价序列的静态特征进行研究，难以描述运价波动的动态特征；二是，尚未从复杂性系统视角对集装箱运价市场进行分析.

已有研究表明，集装箱班轮市场呈现非线性、非平稳、多尺度的波动特征[2]，是一个典型的复杂性系统.复杂网络理论作为研究复杂性系统的重要理论之一，主要通过网络的形式模拟复杂性系统，通过分析网络的整体或部分的统计特性揭示复杂系统涌现的宏观规律，已成功应用于金融、能源、交通运输等领域的研究[5]，为CCFI波动的研究提供了一种新的思路.复杂网络模型实质是拥有复杂拓扑结构特征的图，其关键是确定网络中的点(系统主体)和边(主体间的联系).而符号动力学方法是对一般动力系统的粗粒化处理，为从复杂网络视角揭示时间序列的动态特征提供了有力的工具.如Chao Wang等[6]采用符号动力学方法构建了铜价波动网络.而利用符号动力学方法和复杂网络理论进行CCFI动态波动分析的文献相对较少.

本文采用符号动力学方法对CCFI波动幅度序列进行粗粒化处理，构建了CCFI波动有向加权复杂网络模型，通过计算模态强度及强度分布、加权聚集系数、平均路径长度、模态介数等网络拓扑结构指标，分析了CCFI波动的一般规律，为航运企业及港航管理部门准确把握集装箱运输市场发展、规避市场波动风险提供了一个新的视角.

1 CCFI波动复杂网络模型构建

1.1 CCFI波动符号化过程

选取2003年3月～2018年12月的CCFI月度数据(共190个数据)作为考察对象，数据来源clarkson.将相邻两月CCFI的差值定义为运价波动幅度，即时间t的CCFI值，得到CCFI波动幅度序列，如图1所示.

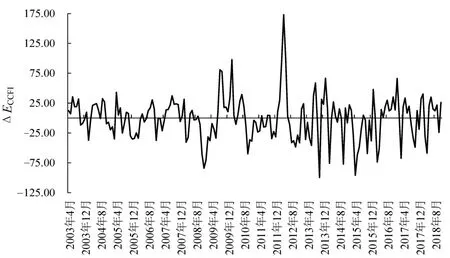
图1 CCFI波动幅度序列Fig.1 Time series of CCFI fluctuation range

时间序列符号化是指对时间序列(或差分等处理后的序列)进行粗粒化处理重构出与原序列长度相同的符号序列.对CCFI波动幅度数据进行粗粒化处理，粗粒化过程充分考虑控制图中“μ±3σ”原则，将运价波动状态划分为异常上涨(H)、正常上涨(h)、持平(m)、正常下跌(l)、异常下跌(L).令每一个波动状态对应一个符号sa，则

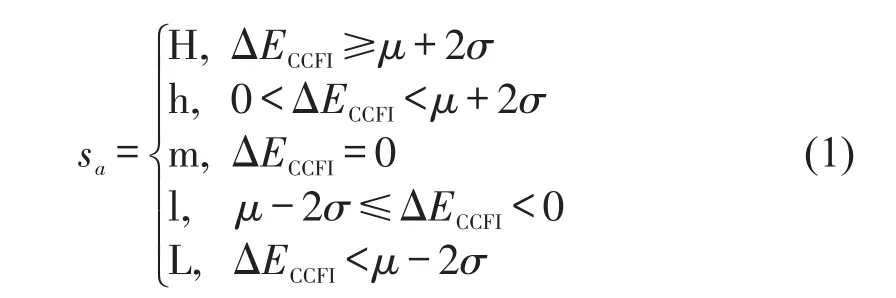
式中：μ为ΔECCFI的平均值，μ=-0.729；σ为ΔECCFI的标准差，σ=36.31；a表示波动序列第a个数值.

至此，CCFI波动幅度序列即转化为对应的符 号 时 间 序 列St={s1,s2,…,sa,…}，其 中 ，sa∈{H ,h,m,l,L}.

1.2 CCFI波动复杂网络构建

考虑到航运运价波动的季节性，以3个月CCFI波动符号作为一个符号序列(称为一个模态)，以1个月为步长作数据滑窗，对CCFI波动符号序列进行粗粒化处理，得到187个CCFI波动模态，如图2所示.理论上sa应组成53=125种模态，但实际共出现26种：{hhh,hhl,hll,lll,llh,lhl,lhh,hlh,llL,lLl,Lll,lhH,hHH,HHh,Hhh,hhH,hHh,Hhl,HHH,hlL,lLh,Lhh,hhL,hLl,Llh,Lhl}.异常上涨H与异常下跌L未同时出现在任一模态组合中，说明每3个月周期内，CCFI波动整体较为平稳，未出现大幅涨落.

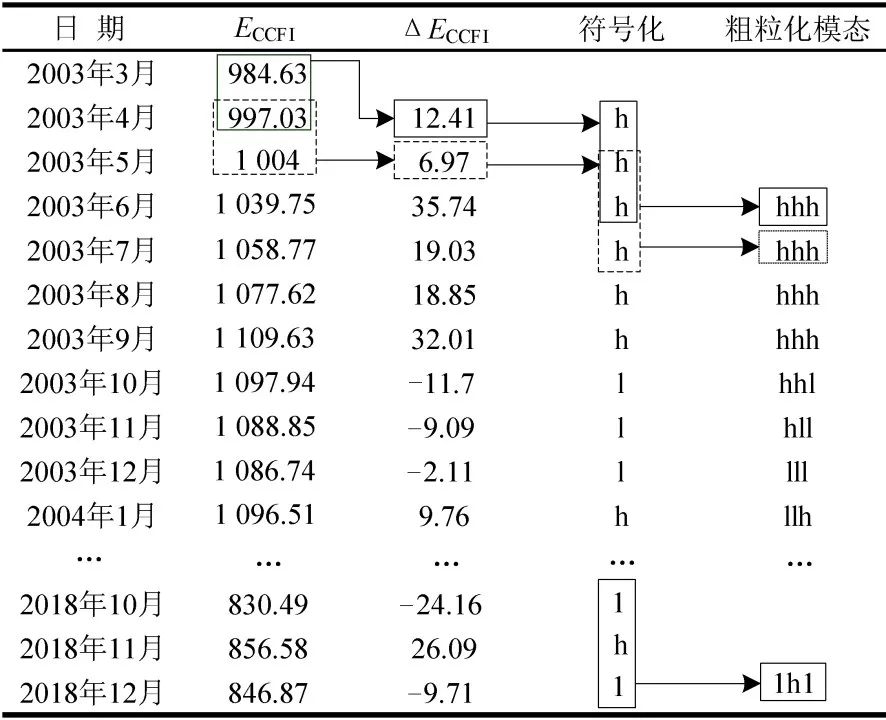
图2 CCFI波动粗粒化过程Fig.2 Coarse graining process of CCFI fluctuation

复杂网络由节点和边构成，以CCFI波动模态为网络节点(若相邻的两模态相同，则不作任何处理)，以模态间转换关系为边，转换次数为边的权重，构建有向加权复杂网络模型，如图3所示，图中节点大小代表模态强度分布数值大小，连线的粗细程度体现了两个模态间边的权重，模态间转换次数越多则连线越粗.由图3可知，关联度较强的6个 模 态 形 成 一 个 闭 环 lll→llh→lhh→lhh→hhl→hll→lll，表明CCFI波动的主要路径是个封闭的环路，经过6个滑动周期的波动又回到该模态，正常上涨、正常下跌是CCFI波动的常态，以逐渐推进的方式进行，即CCFI波动具有渐进性、持续性和周期性.

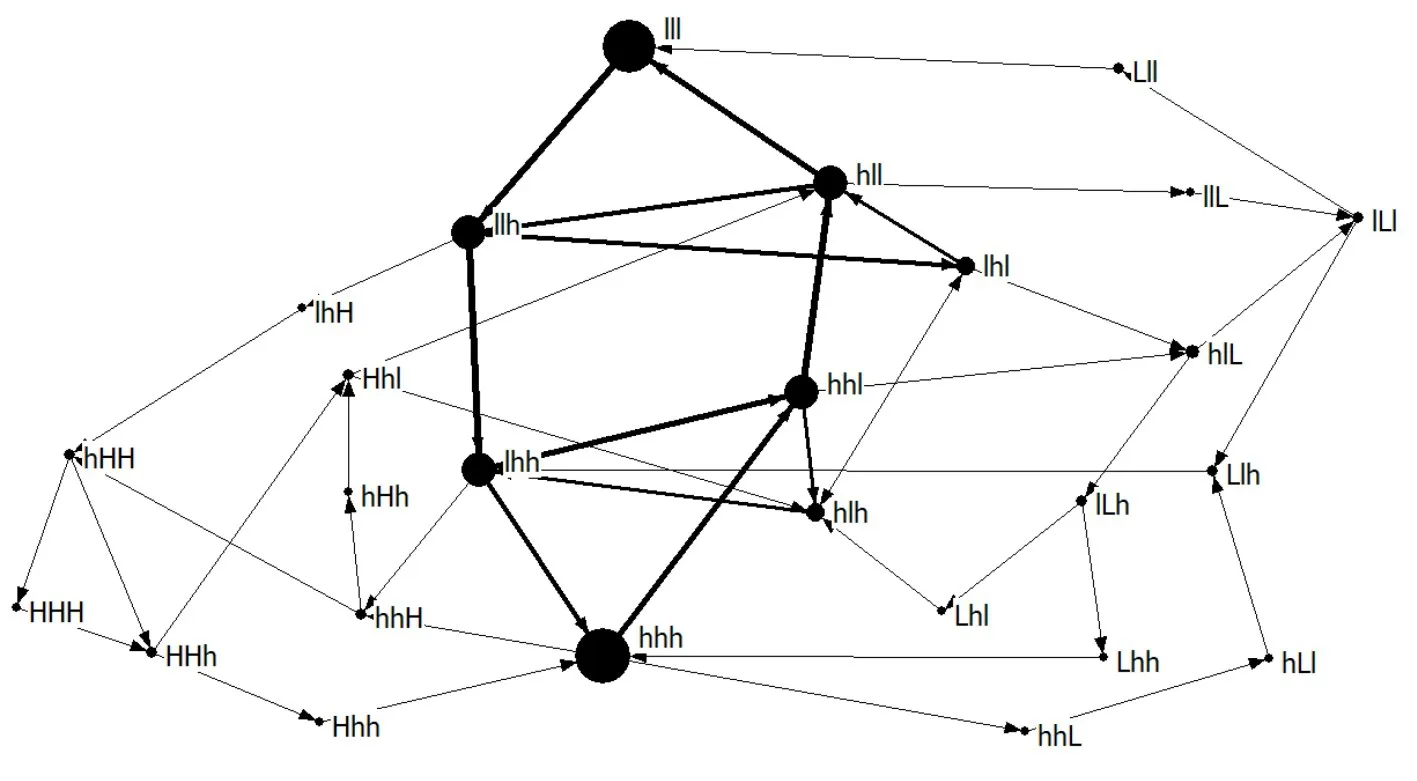
图3 CCFI波动复杂网络Fig.3 CCFI fluctuation complex network

2 CCFI波动规律分析

2.1 模态强度及强度分布

采用点强度对CCFI有向加权波动网络的模态重要性进行分析，既考虑了与该模态相连的邻近模态数，也考虑与邻近模态间边的权重.点强度定义为

式中：Ni为与模态i邻接的由i指向的模态集合；wij为模态i到j的权重.模态强度及强度分布越大，说明该模态在CCFI波动网络中越重要，出现概率及向邻近模态转换概率越大.若网络模态强度分布服从幂律分布，即P(k) ∝k-γ(k为点强度，γ为幂指数)，则为无标度网络.

CCFI波动网络模态强度及强度分布如表1所示.由表1可知：模态hhh、hhl、hll、lll、llh、lhh的点强度值远大于其他模态，累计强度分布达74.87%，说明其在CCFI波动网络中出现的次数及向其他模态转换次数较多，对运价波动传导有重要作用；模态hhh和lll的点强度最大，分别为33，32，表明CCFI连续3个月同向变动(正常上涨或正常下跌)的概率最大，在运价波动中具有最重要的作用；模态hhl、hll、llh、lhh的点强度也较大.相对而言，含有异常上涨(H)、异常下跌(L)的模态出现次数较少.可知，2003—2018年CCFI波动多呈现正常上涨、下跌.

表 1 CCFI模态强度及强度分布统计Table 1 Statistics of mode strength and strength distribution

对CCFI波动模态强度与其排序名次做双对数计算，得到线性回归方程y=-1.22x+3.77，回归系数为0.9，如图4所示.

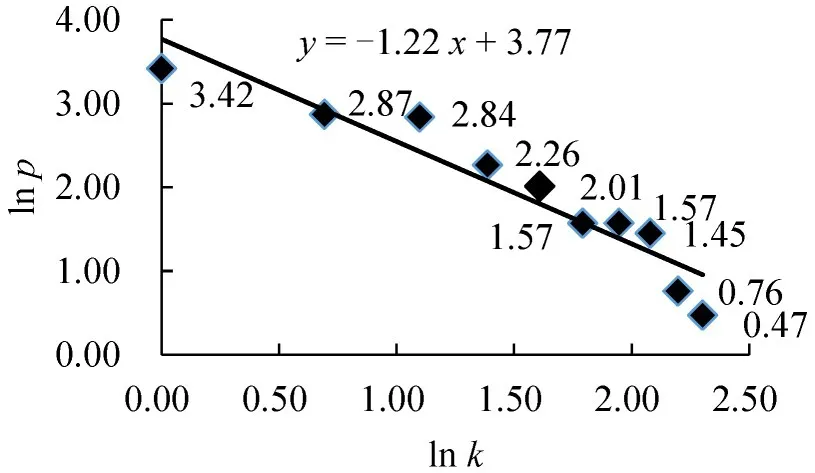
图4 模态强度分布及其排序名次对数关系Fig.4 Logarithmic relationship between mode strength distribution and its rank

由图4可知，CCFI波动模态强度分布具有幂律性，CCFI波动网络具有无标度特性，体现为CCFI波动网络中存在少数强度很高、大多数强度相对较低的模态，CCFI波动主要通过少数重要模态向多数其他模态传导.这可能是因为市场参与者对运价涨跌预判的从众心理，也说明利益驱动下的人为因素或外界突发事件等因素会影响运价波动，一定程度上反映了运价波动的内在动力学特征.

2.2 加权聚集系数

加权聚集系数主要衡量有向加权复杂网络中以模态为核心的局部小范围的关联紧密程度，用于分析模态转换中的核心模态.加权聚集系数越大，说明该模态在网络子群中发挥的作用越大，模态近邻间的关联程度越紧密，反之作用越小、关联度越松散.定义为

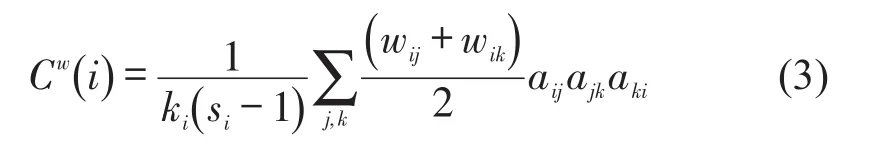
式中：ki、si为模态i的点强度、度值；wij为模态(i,j)间边的权重；aij、ajk、aki分别表示模态对(i,j)间、(j,k)间、(k,i)间是否有联系，有则值为1，无则值为0；aijajkaki表示三个模态间是否相互关联，值为0表示三者不同时相互关联，值为1表示相互关联，构成一个包含模态i的三角形.

CCFI波动网络26个模态的加权聚集系数如表2所示.由表2可知：12个模态的加权集聚系数不为0，前8个模态占比达84.5%；lll模态的加权聚集系数最大(1.167)，其次为llh、hhl、hhH、hll、lhl、lhh、hlh模态，这8种模态在波动网络中作用较大，与邻近模态间关联较紧密，是模态转换中的核心模态.

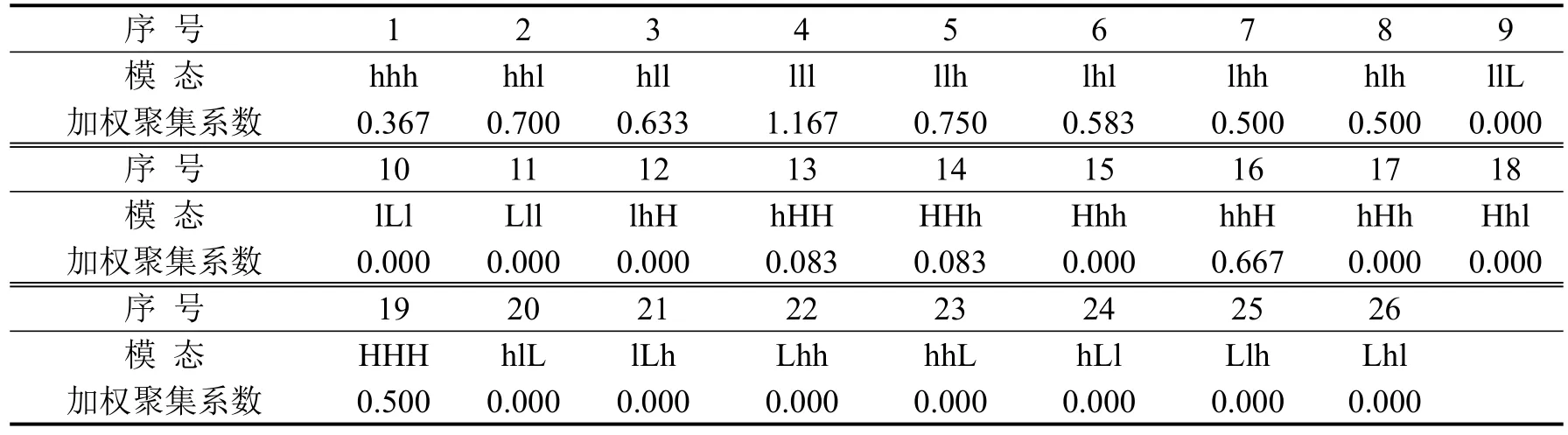
表 2 CCFI波动网络模态加权聚集系数Table 2 Mode weighted clustering coefficient of network

为进一步明确哪些模态之间进行了较多的相互转换，采用n-Cliques方法分析CCFI波动网络中的凝聚子群.当n=2，模态规模大于等于7时，CCFI波动网络共存在8个子群，如表3所示，子群内模态间相互转换的概率较高、转换较频繁，转换距离不超过2步.8个子群根据其模态可分为3类：1、2号子群h、l符号出现次数相当，属于正常上涨、下跌的子群集合；3～5、7子群h符号出现次数较多，属于正常上涨子群集合；6、8子群l符号出现频率较高，属于正常下跌子群集合.

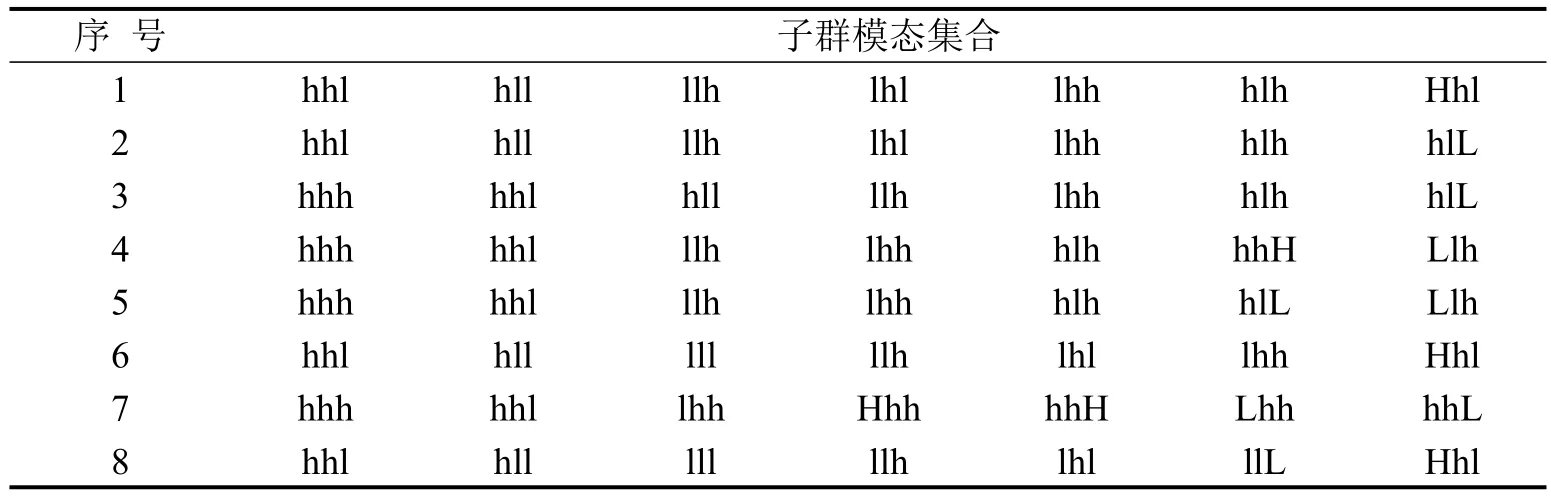
表 3 n-Cliques方法CCFI波动网络凝聚子群集合Table 3 Subgroup set of CCFI fluctuation complex network based onn-Cliques method

复杂网络中，若模态的聚集系数及点强度都较高，则其在网络中具有一定的主导地位.CCFI波动网络模态强度与聚集系数的相关关系分析如图5所示，由图5可知，两者并未呈现良好的相关性，网络表现出较高的复杂性.经济危机、政治事件等影响因素会导致一段时间内CCFI围绕某个模态变动，模态变化对不同影响因素的敏感度亦不同，故表现出复杂的动力学特性.相对而言，lll模态聚集系数与点强度值均较大，在CCFI波动网络中居于核心地位，与邻近模态联系紧密且转换频繁.hhH模态点强度较低、加权聚集系数较大，说明CCFI出现“正常上涨—正常上涨—异常上涨”模态时，波动状态改变的概率较大.

图5 模态聚集系数与强度的相关性分析Fig.5 Correlation analysis between mode clustering coefficient and strength

2.3 平均最短路径长度

平均路径长度L是指复杂网络任意两个节点之间距离的平均值，用于衡量CCFI波动网络模态转换的平均周期，定义为

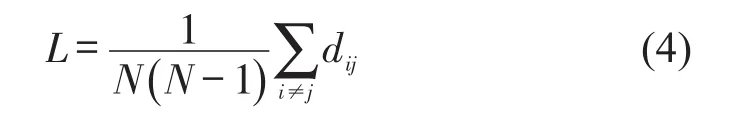
式中：N为网络模态数；dij为模态对(i,j)间的距离(模态对连接所要经过的连边数).

由Uncinet软件计算得到CCFI波动网络的平均路径长度为3.783，基于距离的聚集系数为0.334(范围从0～1，值越小代表聚集性越弱)，加权距离为0.666.较小的平均最短路径长度(3.783)和较大的聚集系数(0.334)，表明CCFI波动网络具有小世界性.CCFI波动模态转换距离概率分布如表4所示，模态转换距离2、3、4、5的概率合计占80.4%，说明模态转换周期较短也较频繁，平均3～4个月转换一次，表现出短程关联性，也为运价未来3～4月的预测提供了依据.

表 4 CCFI波动网络模态转换距离概率分布Table 4 Probability distribution of mode conversion cycle

结合子群分析知，子群内模态间转换周期不超过2个月，关联性较好；但子群外模态间平均转换周期为3.8个月，关联性较差.例如分属子群1的模态hlh(0.5)和子群6的模态lll(1.167)，聚集系数都相对较高，但若要实现转换至少需要3步(lll→llh→lhl→hlh).

2.4 模态介数

模态介数(Betweenness)用于分析复杂网络中模态的信息传递控制能力，衡量模态在网络拓扑结构中的枢纽程度，有利于识别CCFI波动的中间过程.模态k的介数测度wk定义为

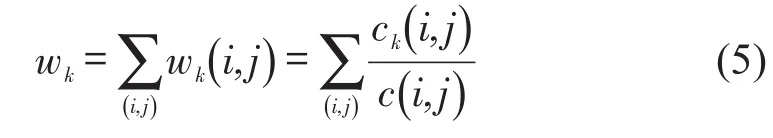
式中：c(i,j)为模态对(i,j)之间最短路径的总数；ck为这些最短路径中通过中间模态k的路径数.

CCFI波动网络的模态介数如表5所示，由表5可知，介数较高的前 8个模态(lhh、hhh、hhl、hlh、hll、hlL、hhH、llh，占模态总数的30.76%)对整个波动网络的介数贡献率达到53.58%，对CCFI波动信息传递具有一定的控制作用，任意两个模态间的转换经过其中转的概率较大.

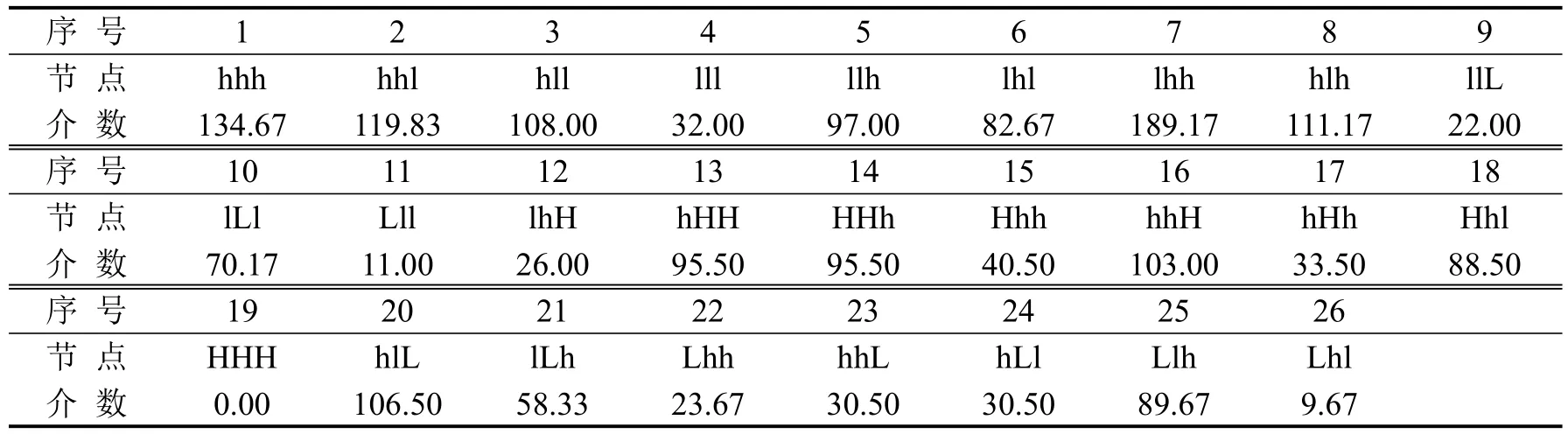
表 5 CCFI波动网络模态介数Table 5 Mode betweenness of CCFI fluctuation network

结合模态强度与介数知，有些点强度高的模态(hhh、hhl、hll、llh、lhh)介数也高，有些点强度较高的模态(lll)介数较低，有些点强度较低的模态(hlh、hlL、hhH)介数较高.点强度高介数低的模态(lll)，表明CCFI波动具有一定的持续性；点强度低介数高的模态(hlh、hlL或hhH)出现时，为CCFI波动的过渡时期，是点强度较高的模态(hhh、lll、hhl、llh等)群簇出现的前兆，可用于预测下一时期的波动模态.

3 结论

集装箱班轮市场作为复杂性系统，引入复杂网络理论构建CCFI波动网络并研究该网络的模态强度及强度分布、加权聚集系数、平均最短路径长度、模态介数等动力学拓扑结构指标，进一步揭示运价波动的动态特征及内在规律.研究表明，CCFI波动网络具有无标度和小世界特性，波动表现出群簇性、周期性、持续性和渐进性.航运企业可根据运价波动群簇性出现及子群内外波动转换周期不同等特点，及时调整市场投放运力规避运价波动风险.此外，应重点关注介数高强度低的波动模态这类市场变动的前兆特征，据此预测运价波动方向，及时采取措施调整市场经营策略.港航管理部门可根据波动规律建立集装箱运价暴涨暴跌预警机制，在集装箱运价异常上涨下跌时及时采取行业补贴、税费减免等调控策略，保障运价市场平稳运行.

本文只对CCFI波动的一般规律进行了初步研究和应用，如何运用复杂网络理论探讨CCFI波动的趋势预测、与外部影响因素的关联关系、传导路径等问题，有待于进一步研究.