城市轨道交通峰前折扣定价方案编制模型
邹庆茹,姚向明,赵 鹏
(1.重庆交通大学交通运输学院,重庆400074;2.北京交通大学交通运输学院,北京100044)
0 引言
高峰拥挤已成为大城市轨道交通面临的突出问题.当运力供给难以进一步提升时,从需求角度加强管理成为缓解客流拥挤的可行措施.差别定价作为需求管理典型策略,已被国外轨道交通广泛用于缓解高峰拥挤,如墨尔本地铁实施的“早起鸟儿票”,07:15前出行免费,约23%的通勤乘客转移至非高峰,有效缓解了高峰拥挤[1].Liu[2]从实践角度综述了各国轨道交通差别定价策略的实施现状.目前,我国北京、香港地铁初步试行了峰前折扣票价政策,但实施效果不明显.因此,有必要探究当前政策的限制因素,以便优化策略提高拥挤疏解效果.
政策实施效果取决于方案是否合理和科学.Douglas[3]等构建基于屋顶模型的高峰分流方法;Whelan[4]基于PRAISE方法研究了不同票价策略对客流拥挤的疏解作用;Lovric等[5]基于出行活动模型评价了低峰票价策略的实施效果;王静[6]对差别定价策略下乘客的出行行为进行了研究;张晓晴[7]构建了适于地铁的双层差异定价模型.相比道路交通,差别定价在轨道交通系统的应用较为滞后,对乘客出行影响机理、定价方案编制方法的研究仍存在很大不足.票价策略具有典型的地域差异性,我国轨道交通差别定价应用尚处探索阶段.本文以北京地铁实施的峰前折扣票价政策为背景,结合前期对乘客出发时间转移弹性的研究基础,进一步研究折扣定价方案编制方法,探究当前票价政策的限制因素,为政策推广提供决策支持.
1 折扣票价对客流的影响分析
揭示票价变动对客流的影响机制是票价方案制定的基础.峰前折扣票价对客流的影响体现在3个方面:影响乘客个体的出发时间;客流在时段间转移,表现为高峰客流向峰前转移;区间流变化,进站流变化间接导致区间流改变.
1.1 折扣票价对乘客出发时间的影响
峰前折扣票价的目的是诱导高峰客流转移,对乘客而言体现在出发时间的前移.ZOU Q.R.[8]以2017年北京地铁实施的峰前五折票价为背景,利用样本聚类、数据挖掘等方法量化测定了不同类型乘客的出发时间转移弹性,可简单理解为出发时间前移概率.这里简要给出本文所需的关键参数,详细研究方法及结果参见文献[8].政策实施6个月后,不同类型乘客的出发时间转移弹性统计结果如图1所示.定义乘客类型为k,类型集合为K,k∈K.为提高统计结果的普适性,假定乘客出发时间转移弹性服从负指数分布,拟合得到转移弹性函数的一般表达式,该弹性是高峰客流转移效果分析、票价方案制定的关键参数,参数拟合结果如表1所示.

图1 不同类型乘客的出发时间转移弹性[8]Fig.1 Departure time elasticities of different passengers
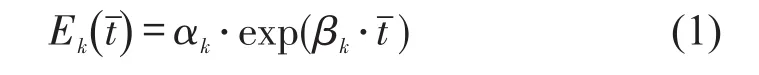
式中:Ek为转移时长为时第k类乘客的出发时间转移弹性;为转移时长,通过乘客出发时间与折扣票价截止时间的差值确定;αk、βk为拟合参数.

表 1 乘客出发时间转移弹性拟合参数[8]Table 1 Parameters for passenger's departure time elasticity function
1.2 折扣票价对车站进站流的影响
基于折扣票价对乘客个体出发时间的影响,从宏观层面分析客流的时变转移过程.图2给出峰前折扣票价实施后车站进站流的变化示意图.将研究时段离散化为子时段(长度为Δt),时段编号为t,时段集合为T,t∈T;折扣截止时段(截止时间紧邻的时段)编号为t*.假设高峰转移客流均转移至t*时段内(此时乘客所花费时间成本最小,与实际统计结果一致).根据时段不同,折扣票价对进站流的影响包含3种情形:①t>t*,客流降低;②t<t*,客流增长,源于票价降低带来的诱增客流;③t=t*,客流增长,包含诱增客流和高峰转移客流两部分.

图2 车站进站量变化示意图Fig.2 Changes of time-dependent station inflows
定义车站编号为i,j,I为车站集合,I={1,…,i,j,…};dit为车站i在时段t内的初始进站量(折扣票价实施前),dit为政策实施后的进站量;θitk为车站i在时段t内乘客类型k所占比例,用于刻画客流结构成分.
(1)情况1.
针对时段t,根据乘客出发时间转移弹性函数推算转移客流量为
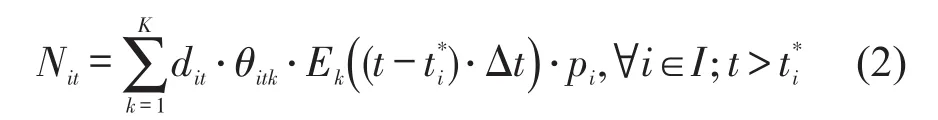
式中:Nit为转移客流量;为车站i实施折扣票价的截止时段;pi为票价折扣比例.
客流向峰前转移后,该时段内进站客流量降低,即
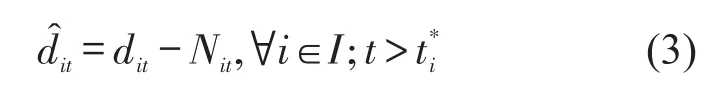
(2)情况2.
鉴于折扣时段较早,票价降低产生的诱增客流较少.在进行诱增客流推算时简化处理,不考虑乘客类型差异,利用宏观的需求票价弹性系数对客流变化进行估算,即
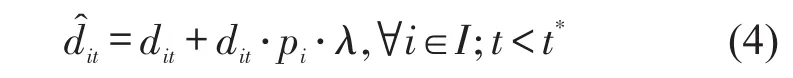
式中:λ为需求票价弹性系数,λ=-0.3[6],负号表示需求与票价的变动成反向关系,具体计算时忽略负号.
(3)情况3.
根据前述假设,高峰转移客流均叠加至折扣截止时段,那么t*时段内客流增量包含高峰转移客流和诱增客流两部分,即
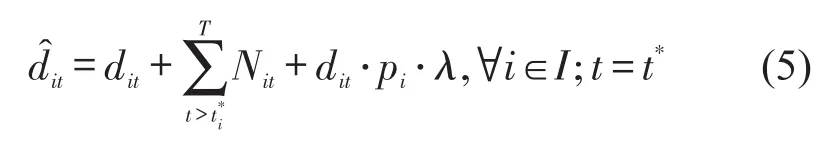
1.3 折扣票价对区间流的影响
在明确折扣票价对车站流影响的基础上,结合车站流—区间流时空映射关系,推算折扣票价对区间流的影响.m为区间编号,M为区间集合;dijt为时段t内由车站i出发去往车站j的流量;φijt为OD流dijt占总进站量dit的比例,刻画客流空间分布结构;qmt为时段t内流经区间m的客流量;用于刻画车站流与区间流的时空关联关系,指时段t′(t′<t)内由车站i出发的OD流dijt在时段t内是否流经(占用)区间m,表示流经,否则表示不流经.将区间m的通过客流看作各OD流dijt在时空上的聚合状态,可表示为
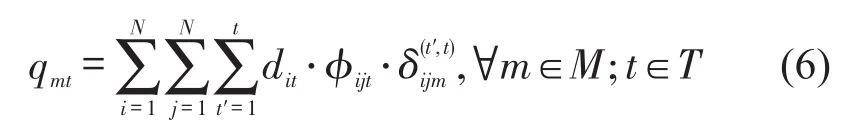
2 模型构建
峰前折扣定价方案包含3个基本要素:折扣时段、折扣比例和折扣车站.折扣时段通过折扣截止时段t*确定;折扣车站由折扣比例确定,若优化结果中折扣比例pi>0,则为折扣车站.因此,模型决策变量为和pi.为提高模型的普适性,假定可实现“一站一方案”精细化定价策略,实践中如需保证车站折扣时段或折扣比例相同,添加简单等式约束即可,可视为该模型的简化问题.
2.1 模型目标
价格策略作为一种柔性需求管理措施,很难完全疏解严峻的高峰拥挤.本文将政策目标定位为高峰拥挤的缓解,具体体现为区间客流拥挤压力降低.当折扣比例较小时,拥挤缓解程度有限;当折扣比例过大时(如免费),可能导致折扣截止时段内大量客流转移,出现峰前次高峰和短时运力虚糜现象.运营企业既希望高峰拥挤尽可能缓解,又希望客流平稳过渡,运力得到充分利用.为此,以一定服务水平下的期望满载率为标尺,以列车满载率与期望满载率偏离度最小化为优化目标(等价于运力运量匹配度最大化).
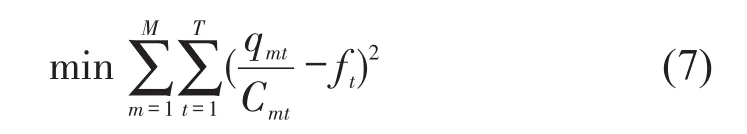
式中:Cmt为时段t内区间m的客运输送能力,可根据列车运行图及列车定员精确确定;ft为时段t内设定的期望满载率,不同时段可差异化设定,取决于乘客可接受服务水平及运营企业的期望.
2.2 模型约束
(1)收益损失约束.
运营企业能承受的收益损失及损失补贴机制是政策推行时考虑的关键因素.以北京地铁折扣票价政策为例,折扣票价实施时间较早(07:00前),诱增客流十分有限.诱增客流带来的票款收入难以弥补折扣票价损失,势造成企业总收益下降.轨道交通乘客边际成本可忽略不计,即增加一名乘客不会对运营成本造成大的影响,故计算收益损失时不考虑运营成本变化,将收益损失近似转换为票款收入损失.不同运营企业的营收现状、补贴机制存在较大差异,很难以固定额度作为限制条件,故以票款收入损失不超过应收票款的一定比例作为约束,即

式中:ζ为运营企业可接受收益损失的上限比例;为乘客出行平均票价.左侧第1部分为客流转移带来的票款损失,第2部分为诱增客流带来的票款收入.
(2)折扣截止时段约束.
折扣截止时段不宜超过车站进站流的尖峰时段,否则会加剧高峰拥挤.ˆ为车站i的尖峰客流时段,需满足
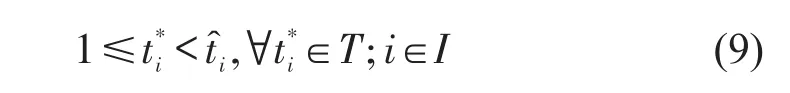
(3)折扣比例约束.
从乘客出行便捷性角度,折扣比例宜设为便于记忆的数值.设定折扣比例的取值范围为{0(无折扣),10%(九折),…,100%(免费)}.pi=1 表示折扣比例为10%,依此类推.折扣比例需满足
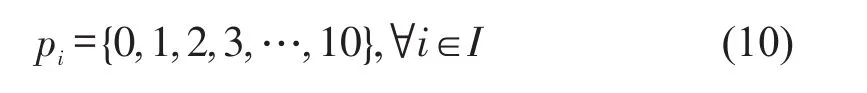
2.3 峰前折扣定价模型
峰前折扣定价方案编制模型完整形式为
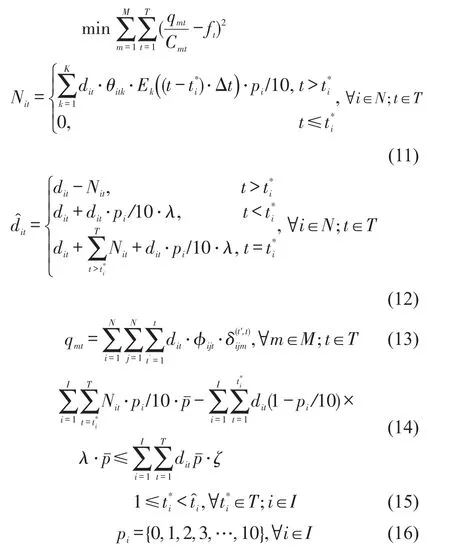
因折扣比例pi转化为0~10间的整数,对模型中相关表达进行了局部修正.式(11)为高峰转移客流量推算关系,式(12)为进站客流量变化关系,式(13)为区间客流量计算表达式,式(14)为收益损失约束,式(15)和式(16)分别为折扣时段和折扣比例约束.模型为非线性纯整数规划模型,但目标函数仅包含二次关系,通用型优化求解器即可快速求解.
3 实证分析
3.1 基本信息
为验证模型的准确性与有效性,以北京地铁八通线为对象进行实证分析.2015年末北京地铁试行折扣票价政策,八通线被选为试点线路(试点车站除四惠及四惠东站),07:00前进站乘客均享受折扣票价优惠.选取政策实施前某工作日自动售检票数据(AFC)为数据源,统计得到分时进站量及客流起讫信息(OD).八通线早高峰拥挤仅出现在上行方向(土桥至四惠),故仅对上行方向进行分析.将八通线换出客流归并至四惠站,得到上行方向完整的客流OD矩阵.
研究时段为06:30-08:30,以10 min为单位将其离散化为12个子时段,编号为1~12.图3给出进线量时间分布特征,可以看出,八通线的进站高峰位于07:40-07:50间(时段8).以实际列车运行图(表号PR1501)为依据计算客运输送能力,分时段运力分布如图4所示.
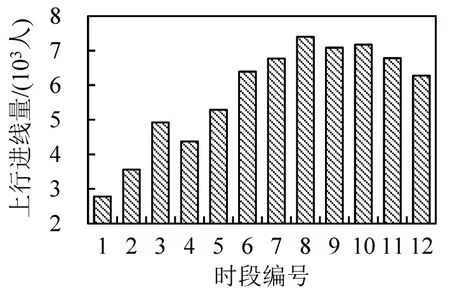
图3 分时进线量分布Fig.3 Time-dependent line inflows
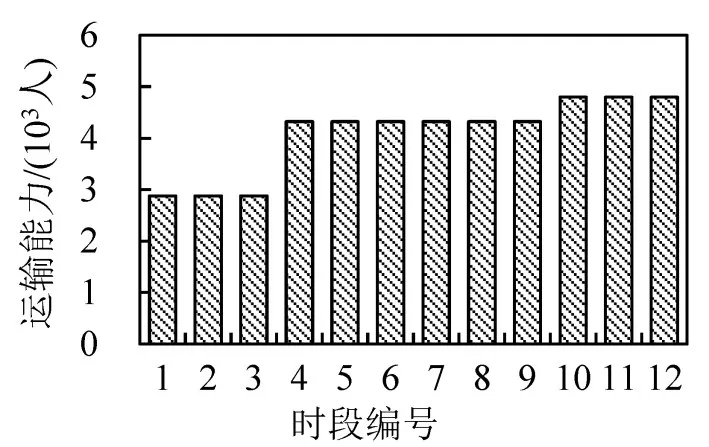
图4 分时客运输送能力Fig.4 Time-dependent transport capacities
模型主要参数取值或来源如表2所示.各站客流尖峰时段取值如表3所示,可以看出,各站客流尖峰均位于07:40以后.

表2 模型主要参数Table 2 Major parameters in model
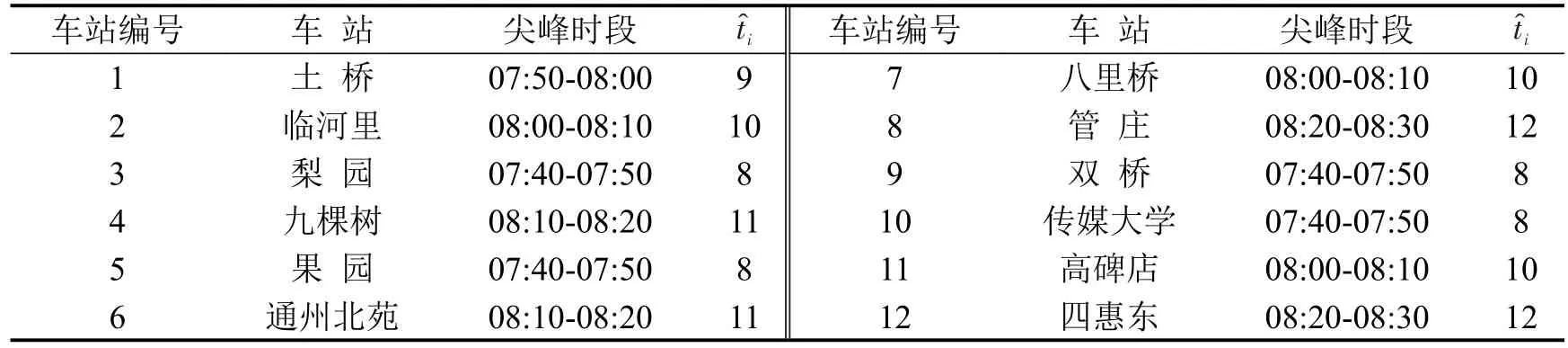
表 3 车站进站流尖峰时段Table 3 Super-peak time of inflows for each station
3.2 结果分析
使用LINGO进行模型求解.为更好地说明定价方案效果,设定5类场景对比分析,如表4所示.不同场景下的对比结果如表5所示,具体定价方案如表6所示.
根据模型目标值及具体定价方案,可以看出:
(1)定时段定折扣方案(场景2,即实际方案)对拥挤的缓解作用较小,与实际方案评估效果一致.
(2)对比场景2和场景3(差异在于折扣比例可变)可知,优化幅度有限,说明折扣比例对拥挤疏解并非关键要素;实际经验也印证这一结论,北京地铁2017年将折扣比例由30%提高至50%,效果仍不明显.
(3)对比场景3和场景4(差异在于折扣截止时段可变)可知,优化幅度明显提升,说明折扣时段是影响票价政策效果的关键因素;前期在进行乘客出发时间弹性研究时发现,乘客可接受的最大转移时长约为30 min,当折扣截止时间过早,将难以对真正的高峰客流产生影响[8];八通线客流高峰位于07:40-07:50,显然折扣票价政策的影响有限.

表4 场景设置Table 4 Information of analysis scenarios
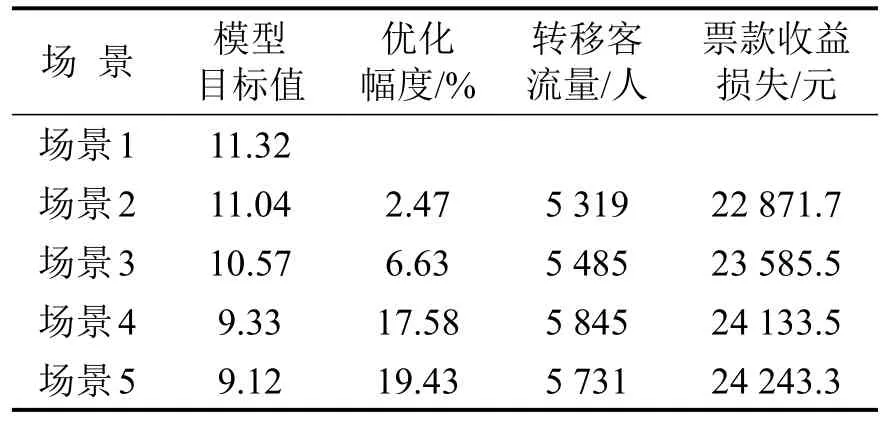
表5 优化结果对比Table 5 Results of analysis scenarios

表6 折扣定价方案Table 6 Pre-peak discount pricing schemes
(4)各场景对应的收益损失差异较小,表明收益损失约束是该模型的限制约束,在运营企业可承受的损失前提下,通过提高折扣比例势必能进一步提高拥挤疏解效果.
综上分析,限制当前政策效果的主要因素在于折扣截止时间过早,难以对真正的高峰需求产生影响,结论与前期乘客出发时间弹性研究结论一致.另外,虽然提高折扣比例能够转移更多的高峰客流,但结合运营企业的营收现状及国外轨道交通已实施的价格差异幅度,五折票价优惠已处于高位水平,建议不再提高折扣比例.
4 结论
本文以北京地铁峰前折扣票价政策为背景,系统研究了定价方案编制问题,构建基于非线性整数规划的峰前折扣定价方案编制模型,以期为定价方案优化提供方法支撑.通过北京地铁八通线实证分析,验证了模型的准确性与有效性,认为限制当前票价政策效果的关键在于折扣截止时间过早.后期政策推广时,应结合客流高峰到达特征合理确定折扣截止时间,不宜进一步提高折扣比例,进而提高高峰拥挤缓解效果.

