弹性工作制和动态停车收费组合策略研究
李 浩,宁煦棋,俞 璐,陈 浩
(同济大学道路与交通工程教育部重点实验室,上海201800)
0 引言
交通需求管理措施可以引导出行者出发时间、路径和方式的选择,实现出行在时间、空间和方式维度上的分散,以达到缓解通勤拥堵的目的[1].有效结合异质交通需求管理措施,统筹优化,治堵效果更显著.停车收费通过设置收费时段、区域和费率影响通勤者的行为选择.通过收集收费实施前后的交通状态数据[2]或通过仿真分析[3]发现,在高峰时段收取高昂的停车费用,会促使出行者调整出发时间.但受制于固定的工作时间,交通量无法在时间维度上充分分散,高峰拥堵仍严峻.弹性工作制则有助于在时间上分散交通流量.在早通勤[4]或早晚通勤链[5]中,通过分析弹性工作制[6]或弹性活动下出行机理[7],发现弹性工作制使交通量分散到更长的时间维度上,起到较好的拥堵缓解效果[8].因此,提出弹性工作制(FWA)和动态停车收费(TPC)的组合管理策略,探究两种策略在拥堵缓解上的耦合效应和组合策略的统筹制定.
1 组合管理策略
首先介绍FWA和TPC的形式及实施范围.选取由核心时段和弹性时段组成的FWA作为研究对象,如图1所示.该制度规定员工在核心时段必须在岗,在弹性时段可以根据自身需求选择在任意时刻抵达或离开单位,每天需保证工作时长.此种形式既能满足员工选择上班时间的自由,又能满足单位的运营要求,在实际应用中被广泛采用.

图1 核心和弹性工作时间组成的FWAFig.1 Working arrangement with core work time and flexible work time
图1中,TSO表示公司开始营业时间,TPA为公司规定必须在岗的开始时间,TPD为在岗时段的结束时间,TEO为公司停止营业时间.TSW表示高效工作的时刻.
为达到高效益,公司开始营业时间应满足TSO<TSW,规定必须在岗的开始时间满足TSW<TPA.同理,必须在岗的结束时间应满足TPD<TEO.Twork表示员工的工作时长,对于所有员工假设Twork固定且相等,另外还需满足:TSO+Twork<TEO,TPA+Twork≤TEO.
FWA在实施中,经常受限于员工单位和岗位性质,很难满足所有员工弹性出行.因此,考虑通勤者部分为弹性员工,其他为上班时间固定的非弹性员工.
TPC方面,考虑通勤者在工作日的停车时间较长,简化定义计费方式为一次性收费,停车费率是随到达停车场的时间变化的连续函数.
2 弹性工作制下动态停车费率优化模型
在FWA和TPC的组合策略下,通勤者通过调整出发时间来避免高峰拥堵和昂贵的停车费用.交通管理者依据出行流量分布情况,调整收费费率,引导通勤者出发时间选择,使得路网总延误最小.将该博弈问题构建为双层规划模型,下层模型描述组合策略下的多用户(弹性员工和非弹性员工)出发时间和路径选择,上层模型以路网总延误最小为目标进行TPC的费率优化.为简化模型,考虑以下假设:
(1)弹性员工与非弹性员工的出行决策相互独立.
(2)不考虑对停车场和出行方式选择的影响.
(3)不考虑出行者的停车巡游时间及停车场容量限制,出行者到达后立即停车并投入工作.
(4)若员工没有在规定的上班时段到达或离开公司,都将产生惩罚费用,且为早到(晚到)和早退(晚退)时长的线性函数.
2.1 多用户出发时间选择模型
选取典型的“家—公司—家”的出行模式构建工作日的活动链,由3个活动(早上居家、上班和晚上居家)和从家到公司的往返通勤组成.
2.1.1 弹性员工的效用方程
弹性员工在TSO之前到达会产生早到费用,迟于TPA到达会产生晚到费用,对于下班离开选择亦同.弹性员工的效用与早上出发时间td1、晚上离开时间td2和选择的路径有关,即

式中:U(1)(k,g,td1,td2)表示早上选择路径k、在时刻td1出发,晚上选择路径g、在时刻td2出发的弹性员工的总效用,由早上居家效用晚上居家效用,可能存在的早到/迟到、早退/晚走的惩罚效用,早晚通勤时间负效用车费用组成;为了区分员工类型,所有变量和参数以上标(1)表示弹性员工,上标(2)表示非弹性员工;分别为早、晚出行的行程时间,是出发时间和路径的函数,下标1表示早通勤,2表示晚通勤;ui(t)表示活动i在[t]时刻的边际效用,i=1表示早上居家,i=2表示工作,i=3表示晚上居家;tsi表示活动i的开始时间;tdj表示出行j的出发时间;η1和γ1分别为早上早到、晚到的效用损失系数;γ2和η2分别为晚上早离开、晚离开公司的效用损失系数;υ为早晚出行的效用损失系数;P(ts2)为ts2时刻的停车收费;βτ为各效用间的权重系数;〈a,b〉-为将a和b进行比较,取较小值.
效用方程描述的活动开始时间和出行的出发时间应满足
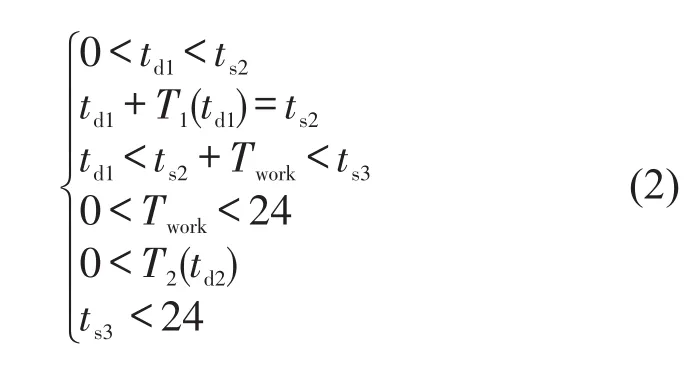
式(2)中依次描述了早上离家时刻应早于到达公司的时刻;早上离家后经过早通勤到达公司,即早通勤时间为正;经过一天的工作Twork和晚通勤后回到家;同时需保证工作时长和晚通勤时间为正.
2.1.2 非弹性员工的效用方程
非弹性员工效用方程与弹性员工相似.不同的是,非弹性员工上下班时间固定,早于或迟于TPA到达都会产生负效用,对于下班行为亦同.非弹性员工的效用同样与早上出发时间td1和晚上出发时间td2有关,表示为
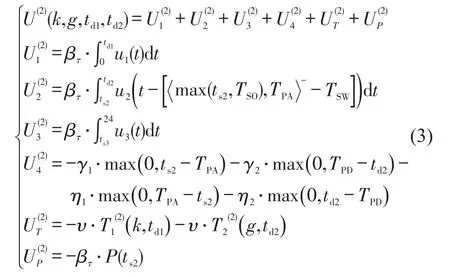
式中:U(2)(k,g,td1,td2)表示早上选择路径k、在时刻td1出发,晚上选择路径g、在时刻td2出发的非弹性员工的效用.
2.2 双层规划模型
在明确弹性和非弹性用户的效用方程后,构建双层规划模型.上层模型中,以路网总延误最小为目标函数;下层模型构建无限维连续时间的变分不等式,以描述用户均衡.
上层模型为

式(5)对弹性员工人数进行约束,将弹性员工所占的比例定义为弹性比例,用θ表示.类型m的员工在OD对(r,s)的总出行量为.当出行总量N为定值时,两类员工的人数和固定,非弹性员工的人数也同时得到约束.式(6)和式(7)分别约束了早、晚通勤中,每个OD对的出行流量全部出发并到达.式(8)约束选择任意路径、任意时刻出发的流量非负.式(10)为出发流量需满足在任意时刻非负的约束.式(11)和式(12)为流量守恒约束.式(13)约束停车收费非负,且不超过规定的最大停车收费Pmax.
根据用户均衡(User Equilibrium,UE)理论,出行者会日复一日的调整出发时刻,最终无法通过改变路径和出发时间而增加全天的活动效用.
综合式(5)~式(7),式(11)和式(12),可以推导出

3 动态费率优化问题求解
3.1 双层规划模型的求解算法
现实路网的停车费率优化问题较复杂,主要体现为多个OD对、多条路径,很难获得解析解,故采用仿真求解SO状态下的收费费率及出行模式,探究组合策略的实施对路网拥堵的缓解效果.相关研究中,缺少通用有效的算法求解双层规划模型.本文基于灵敏度分析的下降算法,将下层模型描述为上层决策变量的约束,将双层规划模型化简为非线性规划模型以便于求解.将上层模型离散并进一步描述为
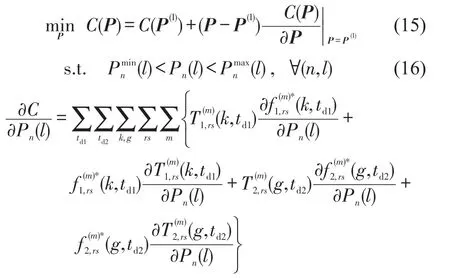

式中:n为停车场编号;h、l为收费时段编号;y为路径编号;分别为第n个停车场在时段l的收费费率、停车收费下限和上限.为了减小计算的复杂程度,假设行程时间不受费率变化影响,即行程时间对停车费率的偏导为0[9].
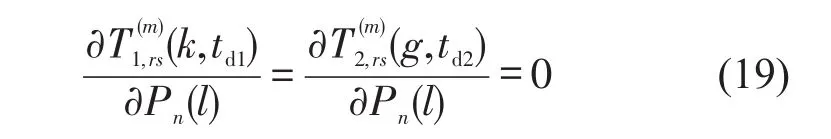
3.2 基于灵敏度分析的下降算法流程
基于灵敏度分析的下降算法流程如图2所示.在求解下层模型时,基于当前的停车费率P(k),采用动态交通分配算法求解UE状态时的出发流量f(k+1)和行程时间.求得f(k+1)后,代入式(17)和式(18)计算∂f∂P和∂C∂Ρ,通过目标函数式(15),得到上层模型中第i+1次迭代的最优停车费率P(i+1).每次迭代后,计算收敛指标G确定是否终止迭代.如满足收敛要求ε,则算法结束,得到最优的停车收费费率P(i+1);如不满足收敛要求,令i=i+1,返回迭代计算.
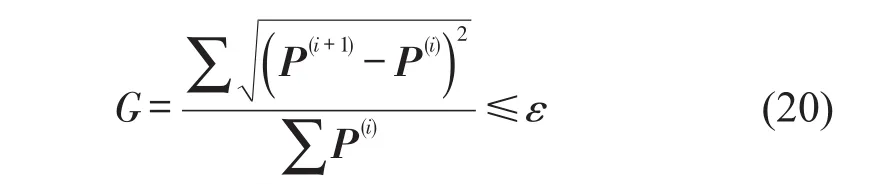
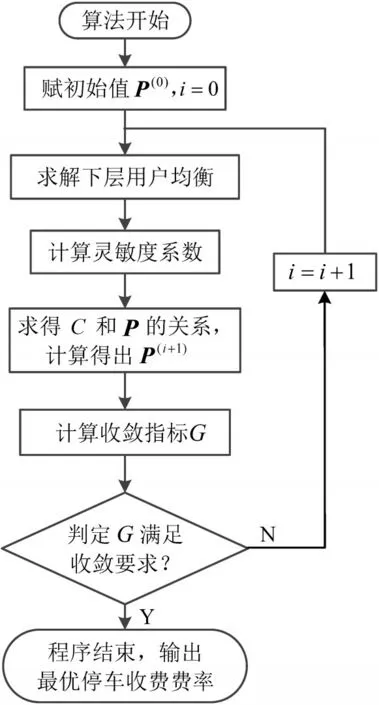
图2 算法流程图Fig.2 Flowchart of algorithm
4 案例分析
将本文双层规划模型和算法应用于图3所示的路网,对不同θ下的停车费率进行优化,对比路网总延误,分析组合策略对路网拥堵的缓解效用.
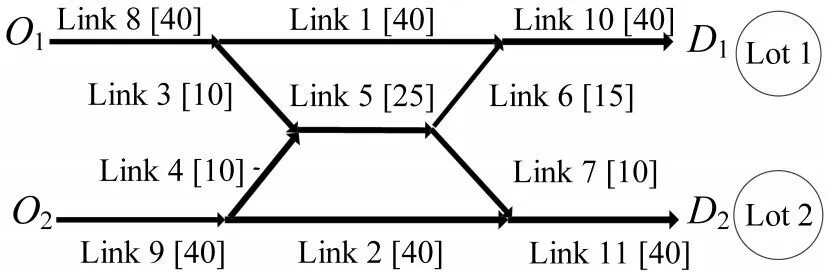
图3 应用路网Fig.3 Hypothetical road networks
案例中,到达D1、D2的员工分别使用停车场1、2.出行需求和路网属性如表1和表2所示.
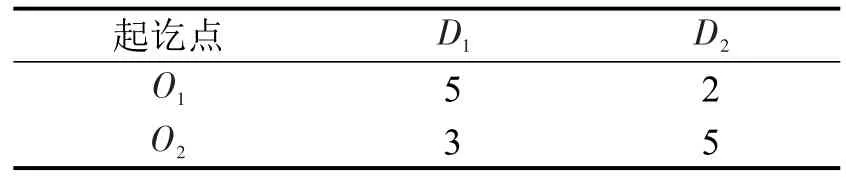
表 1 OD出行需求Table 1 Travel demand in OD (103veh)
晚通勤路网与早通勤路网对称,且通行能力、自由流车速均不变.参考国内外停车收费限制,假设停车收费范围为[0,30]元.

表2 路段通行能力Table 2 Link capacity
居民出行特征参数参考Tseng[10]的调查数据,依据算法流程,仿真模拟出组合策略下弹性员工、非弹性员工和整体路网平均行程时间随θ的变化,如表3所示,以及不同θ下的最优停车费率.可以看出:随着θ的增加,系统路网的人均延误逐渐降低;非弹性员工的延误下降明显,弹性员工的平均延误的降低效果稍弱;当弹性比例增加至50%~60%时,两类员工出行人数相近,员工的行为选择相互影响较大,员工的行程时间均小幅增加.

表 3 不同弹性比例与最优停车费率下的全天平均行程时间Table 3 Mean travel time with varied ratios of flexible workers with parking charges
为了对比组合策略的耦合效用,仿真计算出无、有收费情况下的路网延误作对比,如表4所示.可以看出,组合策略的实施对拥堵的改善效果远大于单独实施其中任意一种制度的效果.在本文的约束条件下(弹性工作时长和停车收费上限限制),单独实施FWA比单独实施TPC的效果好.

表 4 不同管理策略下的路网延误对比分析Table 4 Network delays with different strategies
同时,得出了不同θ下的最优动态停车收费费率和多用户均衡状态下的出行分布.图4列出了θ为20%、50%和80%时,均衡状态下早高峰流量分布和优化的停车收费费率的情况.

图4 不同θ下的早通勤出行分布及优化的动态停车收费费率Fig.4 Morning commute patterns and optimal parking charges with different ratios of flexible workers
对比流量分布图4(a)、(c)和(e)可以发现,两类员工有明显的错峰现象,非弹性员工较集中于中间出行,而弹性员工则更趋于在两侧出行,避开拥堵.结果证明,FWA的实施使得弹性员工调节其出发时间选择,更有利于交通流在时间维度上的分散.
对比停车费率图4(b)、(d)和(f)发现,在任意θ下,高峰时段的停车收费都最高.θ值越高,最优停车费率越低,且停车费率随时间变化更平缓.在弹性工作制规模较大时,较低的停车收费就可以较有效地引导出行,达到很好的分散出行效果.
对比相同弹性比例下的出发流量图和停车收费费率图,如图4(a)、(b),可以发现TPC费率的变化形式和出发流量形式相似,与TPC的优化原则相符合,即对拥挤时段出发的用户收取较高的费用引导通勤者避开高峰出行.
5 结论
提出由核心时段和弹性时段组成的FWA和TPC的组合管理策略,探究两种策略在缓解拥堵上的耦合效应,对动态停车费率和出行模式进行了优化.主要结论为:在FWA和TPC的组合策略下,弹性和非弹性用户有明显的错峰出行现象;FWA和TPC均有显著的分散出行效果,在本文的背景条件下,单独实施FWA的效果好于TPC;在任意弹性员工比例下,最优停车收费费率变化形式和出发流量形式相似,高峰时段的停车收费费率最高;弹性员工比例越高,最优停车费率就越低、费率变化越平缓,同时路网的人均延误越小,弹性工作制可以加强停车收费的拥堵缓解效果;两种管理策略的组合实施效果比单独实施其中一种措施的拥堵缓解效果更好,表明FWA的时间弹性有效释放了固定上班时间对TPC所造成的刚性约束,FWA与TPC的动态调整发生耦合效应,更有效地分散交通出行.
本文在构建模型中,仅考虑了两种管理措施对出发时刻和路径选择的影响,暂无考虑对出行方式选择的影响,同时受限于仿真平台,未能将算法应用于实际路网,后续研究可深入考虑组合管理措施对交通出行结构的影响,并将其拓展至实际路网等.

