对2019年高考数学全国Ⅱ卷理科21题的探究
江苏省灌南高级中学 (222500) 刘鑫钧安徽省淮北市第一中学 (235000) 周宗杰
一、考题再现

(1)求C的方程,并说明C是什么曲线;
(2)过坐标原点的直线交C于P,Q两点,点P在第一象限,PE⊥x轴,垂足为E,连接QE并延长交C于点G.
(ⅰ)证明:△PQG是直角三角形;
(ⅱ)求△PQG面积的最大值.
二、题源及分析
(一)题源
此题是由2011年江苏卷18题改编而来.
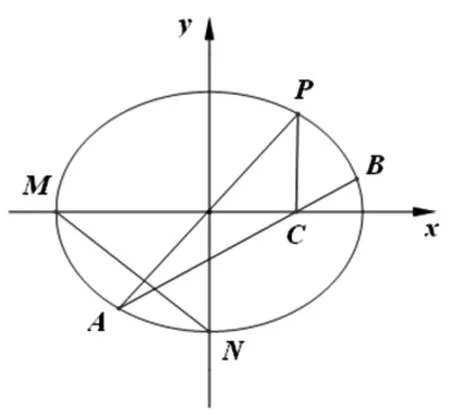
图1
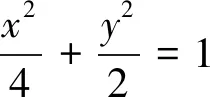
(1)当直线PA平分线段MN时,求k的值;
(2)当k=2时,求点P到直线AB的距离d;
(3)对任意k>0,求证:PA⊥PB.
(二)分析
1.两道高考题的共性主要有四个方面:
(1)两个椭圆方程是一样的.
(2)全国卷Ⅱ后两问的条件与江苏卷的的题干中条件是一致的.
(3)全国卷Ⅱ的第二问表面上是证明直角三角形,实际上只要证明PQ⊥PG,因此与江苏卷的第三问实质上是一样的.
(4)两个高考题均为三问.
2.两道高考题的异性主要有两个个方面:
(1)全国卷Ⅱ不是直接告知椭圆方程,而是以斜率的乘积为定值这一条件呈现,需先求轨迹方程.
(2)从难度上来看:全国卷Ⅱ增加了求△PQG的最值一问,难度增大.
三、解法探究
对于全国卷Ⅱ的三个问题,这里主要探究第二问的解法.
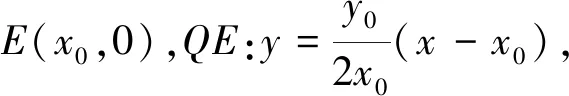
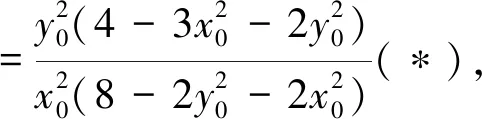
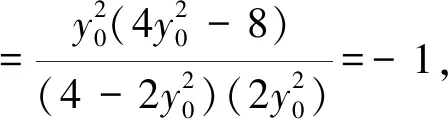
评析:△PQG是运动变化的,但是变化的源头在PQ,它是主动,其它因它而动,是被动的,进一步分析,发现P,Q两点关于原点对称,因此直线PQ动本质就是点P在动,因此可以假设点P(x0,y0).



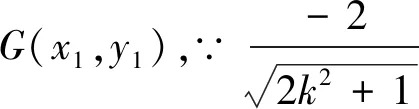


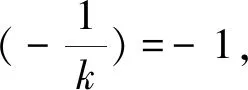
评析:△PQG的变化是由于直线PQ变化导致的,而刻画直线的变化的另一个视角就是通过直线斜率k来刻画,因此假设直线PQ的方程为y=kx是自然的,然后其它变化的点Q,G,E,及直线QG均可用k来表示,这样PQ,PG均能用k来表示,最后直接运算kPQkPG的值,从而获得问题的解答.
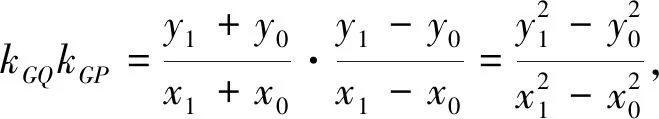
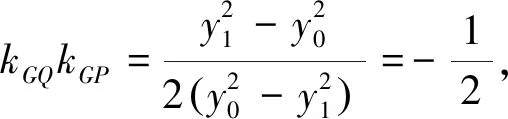
(四)解法4:(几何法)如图2,连接PE并延长交椭圆于P1,由PE⊥x轴,所以P1(x0,-y0),由于P,Q关于原点对称,则Q(-x0,-y0),所以P1Q∥x,P1Q⊥PP1.kGQ=kQE=

图2
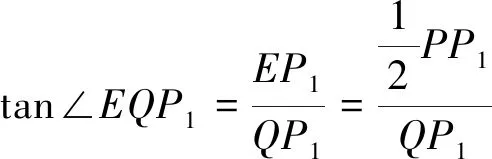

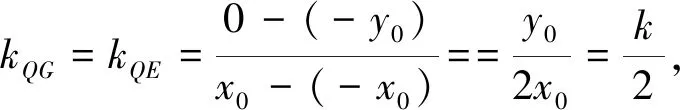
四、教学启示
1.立足变式,深化问题认识
解题教学不仅要一题多解,更要善于多题一解,因此要善于对问题进行变式.顾泠沅等学者把变式教学分为概念性变式和过程性变式教学两类.概念性变式教学突出对概念内涵的理解,过程性变式教学突出对概念外延的应用,注重知识之间的联系和拓展,通过过程性变式教学,使数学教学有层次地递进[1].利用过程性变式可以对一个初始问题进行变式,从而深化对这类问题的认识.
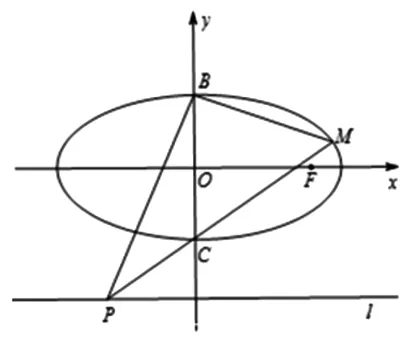
图3
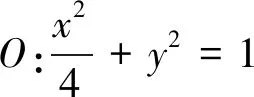


图4
(1)略;(2)若点A,B分别是椭圆E的左、右顶点,直线l经过点B且垂直于x轴,点P是椭圆上异于A,B的任意一点,直线AP交l于点M.(ⅰ)设直线OM的斜率为k1,直线BP的斜率为k2,求证:k1k2为定值;(ⅱ)略
变式不是目的,目的在于要有意识,有目的的引导学生从“变化”中能寻找到“不变”的性质,从而认识到题目的本质,将众多繁杂、凌乱的问题整理为简单、有序的结构,从而减轻学习的压力,这就需要引导学生善于对数学问题进行抽象.
2.基于数学抽象,归纳数学问题
数学抽象是指通过对数量关系与空间形式的抽象,得到数学研究对象.表现在数学概念、命题、思想方法、和知识体系方面的抽象.通过两道高考题的呈现,及两道模考题的变式,给学生提供了一定的实例,那么如何进一步概括抽象出四个试题,将它们从形式上统一起来呢?
经过分析可以看出全国卷Ⅱ高考题中证明△PQG是直角三角形与江苏高考题证明PA⊥PB两题的本质上就是证明斜率之积-1,两道模考题均是证明斜率之积为定值.
因此可以抽象出一个更一般的问题:已知两条直线l1,l2的斜率为k1,k2,λ为实数.证明:k1k2=λ.
3.提炼问题解法,实现忘形得一
高三解题教学,贵在跳出题海,掌握一类问题的普适性解法.经过对这四道试题经过深入的分析,
可以得到一个统一的解法:换k.这种解法一般操作如下:

事实上两道高考题中的解法3和解法4就是换k这一技巧下的具体应用.为了进一步的说明这种解法的普适性,我们以变式1为例.
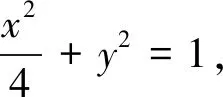

通过以上分析,我们可以看出尽管四个题目中图形不同,所证结论外在之形亦有所区别,但实质上它们可以归一,一种题型,一种解法.
五、结语
G·波利亚有句名言:“发现问题比解决问题更重要”.因此在高三的解题教学中,不仅仅要启发学生多角度、多层次的去思考解决问题,积累数学解题经验,更要善于引导学生发现不同试题之间的区别与与联系,培养学生归纳总结问题,提炼一般模型及解法,从而培养学生的数学核心素养.

