2019年全国Ⅰ卷理科第10题的探究*

福建省莆田第二中学 (351131) 蔡海涛

1.试题呈现

(2019年高考全国Ⅰ卷·理10)已知椭圆C的焦点为F1(-1,0)，F2(1,0)，过F2的直线与C交于A，B两点．若|AF2|=2|F2B|，|AB|=|BF1|，则C的方程为( ).

本题考查椭圆的定义、标准方程及其简单性质，考查运算求解能力、推理论证能力，考查数形结合思想、函数与方程思想、化归与转化思想，考查直观想象、数学运算等核心素养．

2.解法赏析

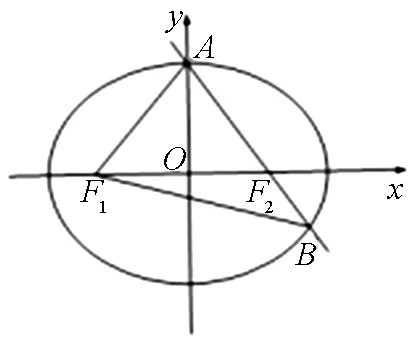
图1

解法1:如图1，因为

|AF2|=2|F2B|，所以|AB|=3|BF2|，又|AB|=|BF1|，所以|BF1|=

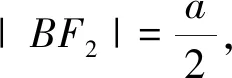
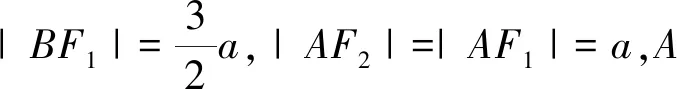
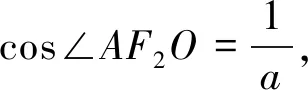
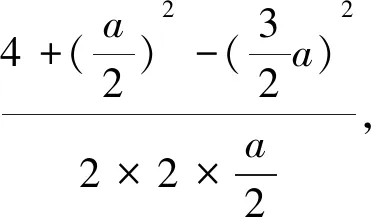
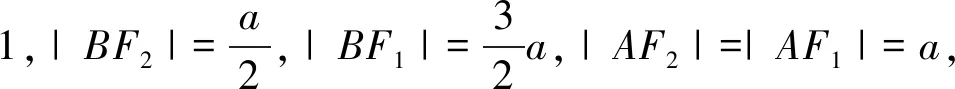
评注:以上两种解法均由椭圆的定义入手，把

|AF1|、|AF2|、|BF1|、|BF2|用a表示，且发现A为椭圆短轴端点.然后抓住两个焦点三角形(椭圆或双曲线上任一点与其两个焦点所构成三角形称为椭圆或双曲线的焦点三角形)△AF1F2、△BF1F2之间的关系(法1)，或是抓住△AF1B、△AF1F2之间的关系(法2)，寻找关于基本量间的等量关系，建立关于基本量的方程，求得a的值，进而求得椭圆的方程.一般地，涉及焦点三角形的计算常常利用定义入手，两个焦点三角形的问题往往要发现这两个三角形边、角的关系.

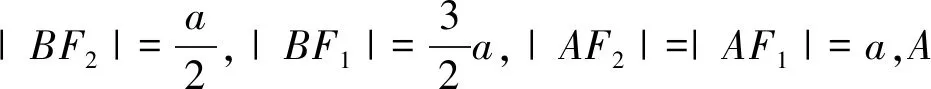
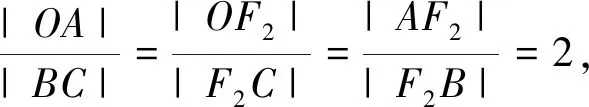
评注:解法3和解法4均考虑先求出点B的坐标，然后代入椭圆的标准方程求得a的值.两种解法的区别在于求得点B的坐标方法不同，解法3利用向量方法，解法4利用平几方法.在解析几何的运算中，要注意平面向量的工具功能.

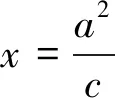
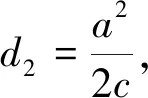
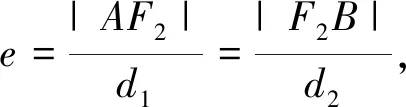
3.背景探究

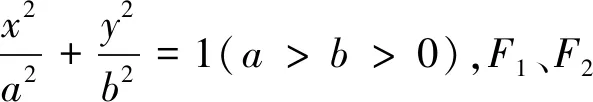
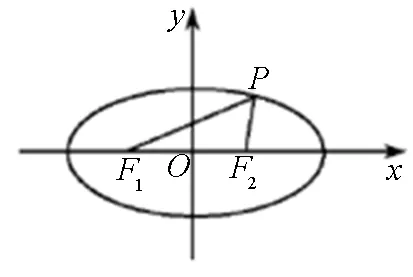
图2

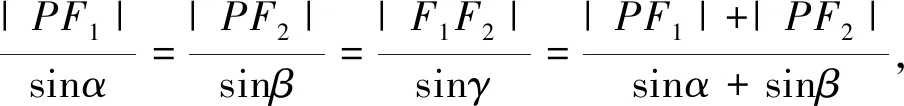
下同解法1.

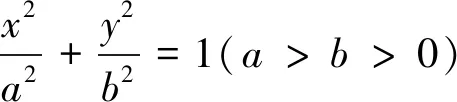
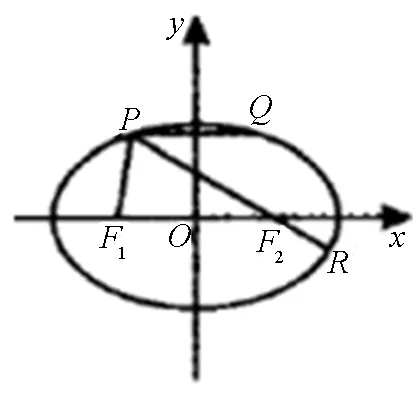
图3

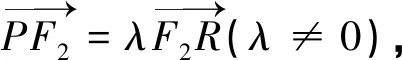
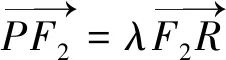
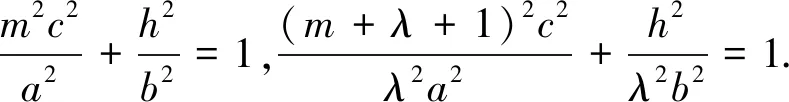
同理，可证双曲线有相同的结论.

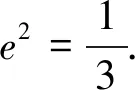
荀况说过：“不登高山，不知天之高也；不临深谷，不知地之厚也；不闻先王之遗言，不知学问之大也.”正如荀况所说，近几年数学高考试题的命制也从更高的观点展望和突破.[1]一道看似平淡无奇的高考题，若我们加以探究，可能会发现一题多解那片“美丽的风景”，再由特殊推广到一般，探究其命题的背景，则我们更能把握问题的实质，更好地统领问题的全局.