在概念复习中提升数学核心素养*

安徽省界首第一中学 (236500) 赵天玺 朱庆斌

一、问题提出

有种很有道理的说法：“平时教学是栽活一棵树，复习过程是育好一片林.”可见复习课是课堂教学中的重要一环.目前高三数学复习在某一章节或某一单元内容的第一个课时，教师通常会把所有的相关知识进行“梳理”.概念复习主要是放在“知识梳理”这一块，通常是把概念设计成填空题，让学生填写关键词.按照这种教学流程，教师仅把数学概念复习当作概念的简单再现，况且由于时间仓促，有些数学概念还没来得及记住就过去了，更谈不上对概念的再理解，这样的概念复习效果可想而知.怎样做好概念复习，提升学生的核心素养，本文将通过两道模考题的讲评案例，给出笔者的教学思考.

二、教学案例

案例1 已知实数x，y满足约束条件

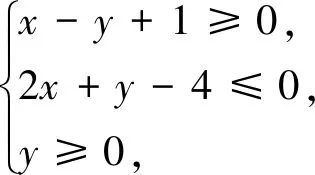
师：模考中这道题做错的同学比较多，现在请做错的同学说说考试的时候你是怎样思考的？

生1：一开始看到这道题，以为是个线性规划题，画出了可行域，可目标函数不是线性的，不知道如何下手，最后还是没有做出来.

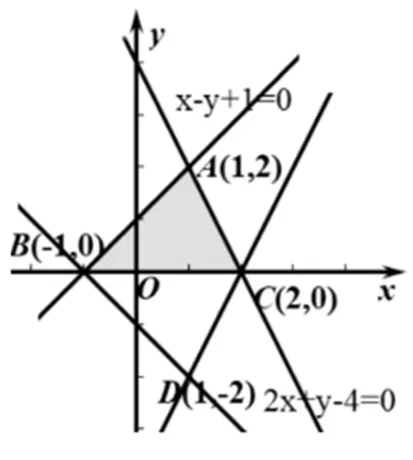
图1

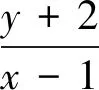
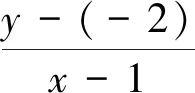
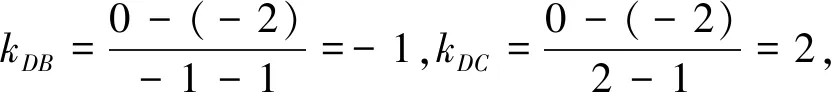
师：不对的原因还是你没有真正理解概念的本质和内涵.现在我们一起梳理一下“斜率”这个概念，什么是直线的斜率？

众生：斜率是衡量一条直线倾斜程度的量.它通常用倾斜角的正切值，或两点的纵坐标之差与横坐标之差的比来表示.

师：那么什么是直线的倾斜角？它的变化范围是什么？倾斜角取何值时，斜率不存在？

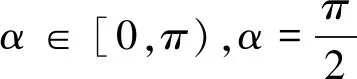
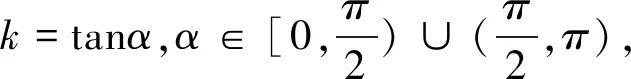
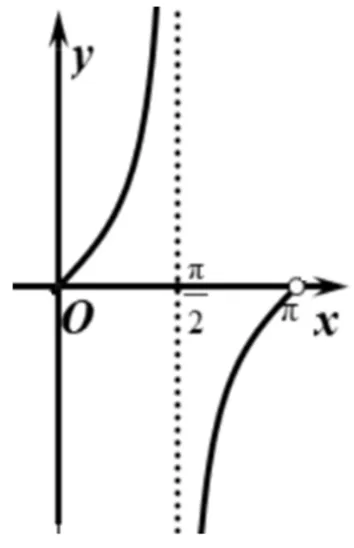
图2

生4：不是.

师：不错，我们只能说它有两个增区间，而在两个区间的并集上不是单调递增的，这一点是同学们容易产生错误的地方.题目要求点(x,y)和点(1,-2)连线l斜率的取值范围，是不是应该先把l倾斜角的变化范围找出来？

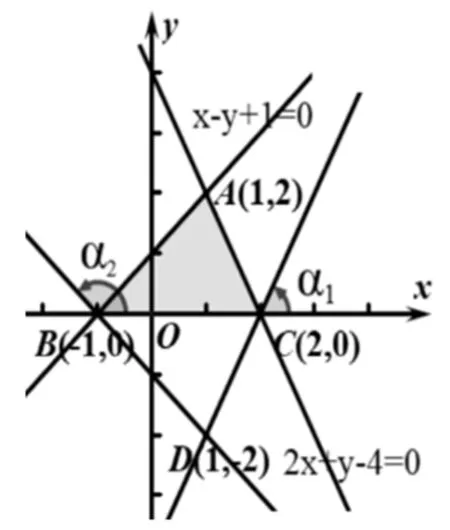
图3

众生：是的.

师：我们来一起找，如图3，当点(x,y)位于点C(2,0)时，此时倾斜角是锐角α1，且tanα1=2，点(x,y)向左运动时l的倾斜角变大，点(x,y)位于点B(-1,0)时l的倾斜角α2最大，是钝角，且tanα2=-1，所以l倾斜角α∈[α1,α2].要求l斜率的取值范围下一步该怎么做？

师：不错，现在请生2重新做一遍这个题目.

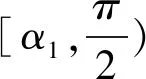
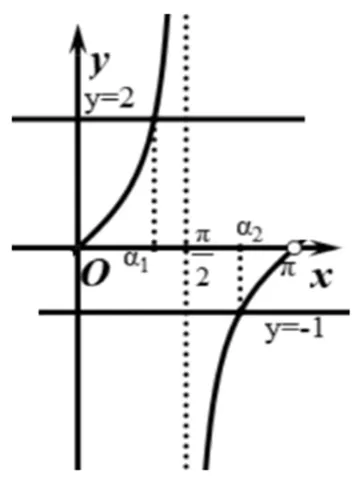
图4

综上y∈(-∞,-1]∪[2,+∞).

师：很好.现在明白考试时做错的原因了吧？

生2：明白了，我把斜率在区间[α1,α2]上当作单调递减的了.

师：看来同学们对数学概念特别是像“斜率”这样的数学核心概念本质和内涵的理解有待进一步地加深.

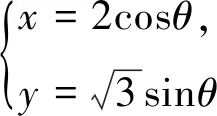
(1)求曲线C1的普通方程，曲线C2的直角坐标方程;

(2)设直线l：y=x与曲线C2交于M、N两点，过F(-1,0)作与直线l垂直的直线交C1于P、Q两点，求四边形MPNQ面积.

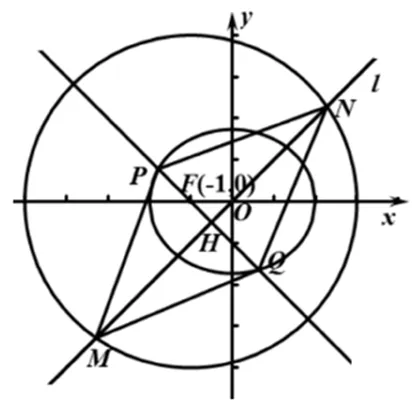
图5

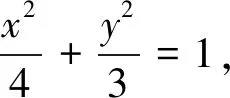
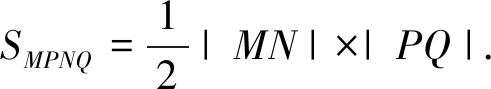
师：先别急，你怎么知道四边形MPNQ是个菱形？它的对角线互相垂直平分吗？

生2：H点不是QP的中点，四边形MPNQ不是菱形.

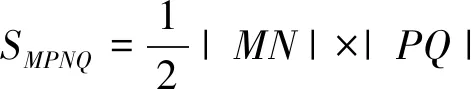
师：还有其他求弦长的方法吗？

生3：求直线与圆相交于的AB时，|AB|=

师：很好，还有其他的方法吗？

生4：还可以用直线的参数方程来求，具体公式想不起来了.

师：好吧.看来同学们对弦长的求法，掌握的并不全面.弦长实质就是两点间的距离，现在我们有必要把平面解析几何中“两点间的距离”及其相关概念深入梳理一下.

师生一起画出概念知识导图(图6)，按照导图依次梳理有关概念、公式及方法.

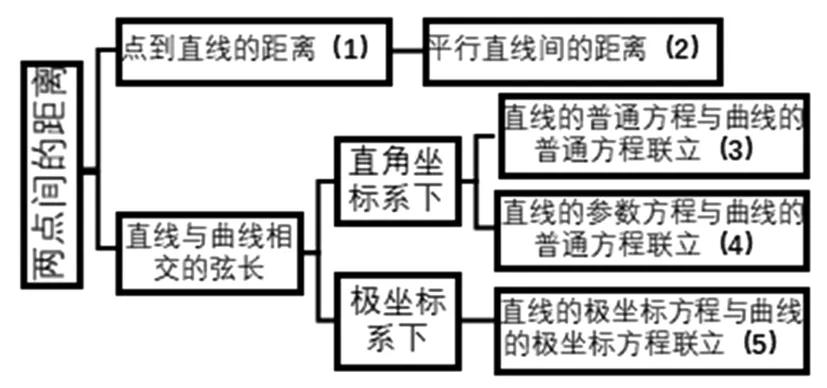
图6

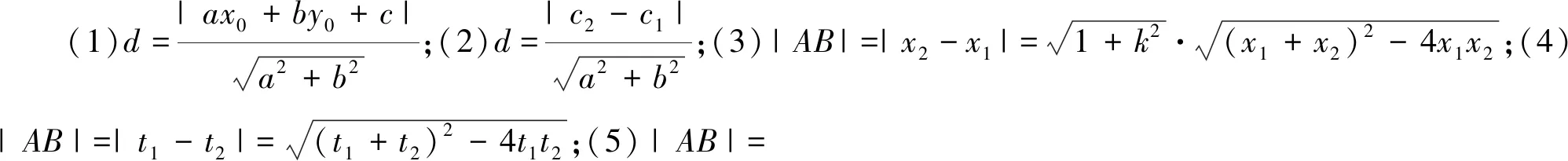
师：现在请同学们在直角坐标系下，用不同的方法求弦|MN|.

生6：(法二)利用直线与圆相交的弦长公式

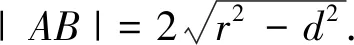
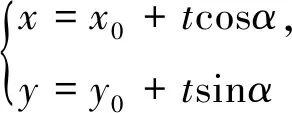
师：很好，现在说说极坐标系下怎样求弦|MN|.

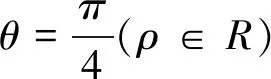
师：上面的四种方法，是否都能用于求弦|PQ|.

众生：法二不行，因为曲线C1不是圆.

师：是的，请同学们用其他三种方法求弦|PQ|.

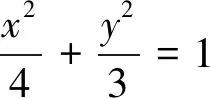
其他的学生纷纷表示遇到相同的问题.

师：这样真的不容易得出结果.怎样才能不必求出θ1、θ2，就可以求出弦|PQ|.

生10：由公式(5)只要θ2-θ1=0或π，极点在直线PQ上即可.

师：原题目中的极坐标系极点在原点，不在直线PQ上.怎样建立极坐标系才有利于问题的解决？

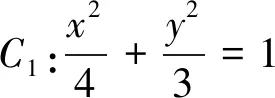
众生：这样建立的极坐标系来求|PQ|比用公式(3)、(4)简单多了！

师：简单是建立在以“两点间的距离”为核心的概念知识体系全面掌握之上！最后易得SMPNQ=

三、教学思考

1.概念复习要立足于对概念本质的深度理解

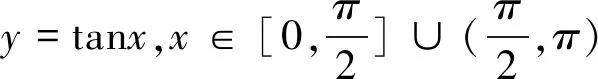
2.概念复习要致力于建立相关概念间的内在联系

学生数学能力不强的主要根源在于没有掌握数学基本概念及其联系方式，概念复习要加强概念联系性的教学，从概念的联系中寻找解决问题的新思路——解题的灵活性并不来自于“题型+技巧”，而是来自于概念联系通道的顺畅.

案例2中，学生求直线与曲线相交的弦长时，方法单一，思路不畅，运算出错，其根本原因是概念不清，概念联系通道不顺畅，概念知识体系不完备.其实弦长概念的本质就是两点间的距离，笔者带领学生构建知识导图，复习了由这个概念生产或导出的相关概念，掌握了求弦长的各种方法，构建了以“两点间的距离”为核心的概念知识体系.高三概念复习要考虑前后概念之间的联系，打破章节界限,根据概念发生发展的脉络，不断重建、重构，充实和完善，沟通相关概念之间的联系，建立相关概念完备的知识体系.

四、结束语

概念复习是概念教学不可或缺的重要环节，是高三复习的重要内容.概念复习要贯彻于高三复习的各个环节，可以在知识回顾、例题讲解、试卷评讲中穿插进行.随着概念复习的推进，学生就会对概念理解越来越本质，对概念知识体系掌握越来越系统，从而促进学生对数学本质的把握，提升学生的核心素养.