积累基本活动经验 落实数学核心素养

于涛

[摘要]文章以“两角差的余弦公式”教学设计为例，创新教学活动，从几何直观到代数推理，引导学生经历数学实践活动和思维活动，积累基本活动经验，培养数学核心素养，

[关键词]基本活动经验;核心素养;两角差的余弦公式

《普通高中数学课程标准（2017年版）》指出：通过高中数学课程的学习，学生能获得进一步学习以及未来发展所必需的数学基础知识、基本技能、基本思想、基本活动经验（简称“四基”），《课标（2017年版）》将“双基”提升为“四基”，首次提出基本活动经验是数学学习的基础，史宁中教授认为，数学活动既应包含具体身体行动的活动，也应包括数学思维活动，这样基本活动经验主要就是两个经验：一个是学生的实践经验，培养学生的数学直观：另一个是学生的思维经验，培养学生会思考问题，因此，数学基本活动经验渗透在整个数学教学中，成为落实数学核心素养的有效途径，下面以“两角差的余弦公式”为例，谈谈通过恰当创设教学活动，引导学生积累基本活动经验，培养数学核心素养。

1基本情况

1.1教材内容分析

两角差的余弦公式是在学习三角函数、向量等知识后，研究的第一个两个角的三角计算公式，它是研究其它两角和差公式、倍角公式的基础，具有承上启下的作用，从知识生成的过程看，本节课的知识源白天文学的测量问题，涉及几何图形的长度、面积、角度等度量问题，从推导公式的过程看，需要应用单位圆等数学模型，联系三角函数、向量等知识。

1.2学生学情分析

学生在初中学习了用直角三角形定义锐角三角函数，在高中学习了用单位圆定义任意角三角函数，从静态的锐角到动态的任意角，学生先后学习了两个重要数学模型：直角三角形和单位圆，但还不能将解决角的问题与应用数学模型相结合，另外，学生在初中学习勾股定理及其证明时，初步体会了将几何图形的相互关系（面积关系）转化为代数表示（勾股定理），具备了一定的直观想象意识。

1.3教学目标设置

（1）借助勾股定理的证明方法，回顾用几何图形的相互关系研究代数关系的基本思路，发展学生提出问题的能力：

（2）结合活动探究，经历从几何直观到代数表示，初步得到两角（锐角）差的余弦公式，培养几何直观素养：

（3）会用任意角的单位圆模型证明两角差的余弦公式，感悟从具体到抽象、特殊到一般、数形结合等基本思想，培养逻辑推理素养：

（4）通过例题及变式的教学，掌握两角差的余弦公式，培养数学运算素养：

（5）借助探究性作业，深化基本活动经验，发展学生的创新意识，

重点：两角差的余弦公式，

难点：两角差的余弦公式的生成与推广过程，

2教学过程

2.1复习回顾，创设情境

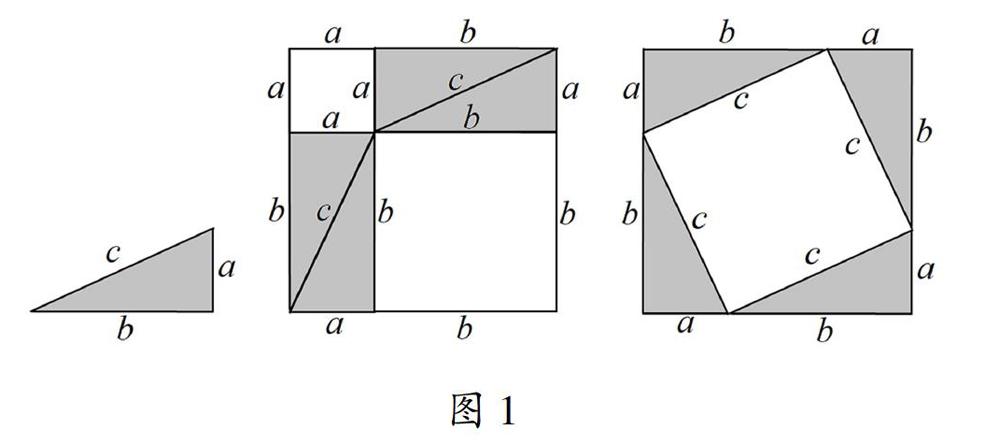
问题1如图1.说说初中课本勾股定理证明方法的思路和基本思想？

学生：用四个全等Rt△构造出两个全等正方形，根据两个图形中阴影部分和空白部分的面积分别相等，得到a²+b²=c²体现了数形结合的基本思想。

教师：这个方法体现了形数统一，既严密又直观，

问题2几何图形的度量和计算除了长度、面积，还有角度，如图2.若直角三角形斜边长为1.其中一个锐角为θ，请仿照勾股定理的证明思路，说出有关θ的等式。

学生：平方关系sin²θ+cos²θ=1

教师：不过这个几何图形（图2）只能证明锐角平方关系，要证明任意角平方关系需要用单位圆模型。

设计意图

勾股定理的证明是通过对几何图形的拼接、割补来证明代数关系的，证明过程重在通过对几何图形的度量和计算，将几何关系转化为代数表示，是以形证数的典范，以此唤醒学生直观想象的意识，鉴于几何度量不仅包含长度、面积，还包含角度，通过相同图形，不同代数观测，得到不同的代数表示，培养学生学会用数学的眼光观察几何图形，发展学生提出问题的能力，从长度到角度，用图1、图2分别证明勾股定理和平方关系（锐角）的思维过程是类似的，是探究发现两角（锐角）差的余弦公式的重要活动经验。

2.2合作交流，探究发现

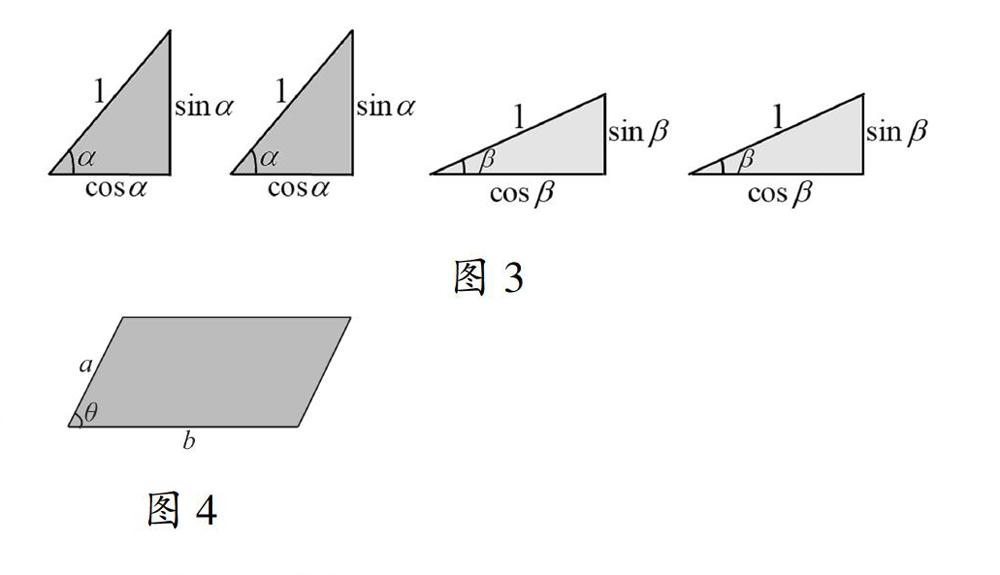
活动：请用两对斜边长为1的直角三角形（如图3），其中一对含锐角α，另一对含锐角β，仿照勾股定理的证明思路，探究有关α与β的等式，（注：学生每人两对直角三角形，同桌为一组）

公式：平行四边形面积公式（如图4）：S□=absinθ

探究结果展示：（请一个小组分享，简述证明思路）

教师：这个公式就是两角差的余弦公式，但是只证明了α和β是锐角的情形。

设计意图

活动的创设是问题2的变式，从四个全等直角三角形的一个锐角的等量关系的发现，到两组全等直角三角形的两个锐角的等量关系的探究，让学生经历证明勾股定理的思维过程，积累通过几何图形发现数学结论的活动经验，培养学生几何直观素养，从一个角到两个角，让学生感悟数学问题产生、发展的方法，发展学生发现、提出问题的能力，

2.3推导证明，公式推广

问题3如何证明对任意角α，β∈R，cos（α-β）=cosαcosβ+sinαsinβ？

教师：我们用直角三角形的三边关系定义了锐角三角形函数，探究活动用直角三角形拼接几何图形证明了两角（锐角）差的余弦公式，要将其推广至任意角，说说你的想法？

学生：可以考虑用单位圆模型来证明，

教师：如图6.分别画出角α，β的终边，写出终边与单位圆交点A，B的坐标，那么，角α-β如何在图中表示？（根据学生的回答，出现了两种思路）

设计意图按照初、高中學习三角函数定义的顺序，先用直角三角形拼接几何图形进行公式的探究与发现，再用单位圆模型进行公式的推广与证明，从具体到抽象、特殊到一般，符合学生的认知规律，对于两种证明方法，思路一代数多于几何，紧扣学生学习的最近发展区，联系向量、诱导公式等知识，发展思维的严谨性：思路二几何多于代数，注重对几何问题的图形分析，探索解决问题的思路两个证明思路注重学生的数学思维活动，从数学直观向理性思维转变，培养学生的逻辑推理素养。

设计意图例1、例2、例3三个例题的设置，从具体角到字母角，再到具体角与字母角的混合，帮助学生理解运算对象的变化，重在巩固基本知识，变1、变2分别将例2、例3的单个角换成复杂角，重在运算思路的探寻，提升基本技能，强化换元等基本思想，例题和变式形成有机整体，培养学生数学运算素养。

2.5作业布置，拓展探究

（1）将课堂探究图形中角α的余角记为α，请探究有关α与β的等式。

（2）若将两对斜边长为1的直角三角形拼成如图9所示的矩形，请探究图9中空白部分菱形面积的含义。

（3）（选做）你还能用这些直角三角形拼出其它常见平面图形，并根据其几何关系探究代数关系吗？

设计意图探究（1）是课堂活动的延伸，探究结果是两角（锐角）和的正弦公式;探究（2）给出了第三种矩形的拼接方式，根据标注角的不同，探究结果可能是两角（锐角）差的正弦公式，也可能是两角（锐角）和的余弦公式，通过探究（1）（2），启发学生的思维，帮助学生强化基本活动经验，为其它公式的学习做好铺垫，培养直观想象素养，探究（3）在探究（2）的基础上，具有较大的开放性，旨在培养学生的创新意识。

3教后反思

3.1实践活动重数学直观

关于三角公式的学习，学生往往更关注公式的实用性，忽略对三角公式的理解，因此，本节课的教学设计，从整体教学设计理念出发，将三角知识的学习放置于整个初、高中相关知识的学习中，以学生认知发展规律为依据，围绕几何图形构建实践活动，其中，在创设情境、探究发现和探究作业等教学环节，探究对象的几何图形和代数要素不断变化，强化和丰富了学生的实践活动经验，不难发现，每个几何图形都体现着相应代数表示的一种几何意义，有助于学生加深对公式的理解，积累数学实践活动经验，有助于学生数学直观的培养，发展学生发现数学结论的能力和意识，让学生自然地学习知识。

3.2思维活动重数学推理

不论是证明公式，还是应用公式，都是用已有数学知识解决数学问题的过程，都应帮助学生发展数学思维，因此，对于公式的推广與证明，教学中不急于陕速完成，而是通过精心设置问题，引导学生积极思考，遵循最近发展区理论，探寻较为自然的证明思路;对于公式的应用，教学中以题组、变式等方式，题目设置由简至繁，将解题经验逐步归一，构建科学思维体系，积累数学思维活动经验，就要在教学活动中，引导学生将调动基础知识、施展基本技能、应用基本思想有机融合，积累解决数学问题的经验，完善认知结构，发展自动自觉的思维意识。

总之，教学中既要关注实践活动，也要关注思维活动，它们是基本活动的两个侧面，与其它“三基”紧密联系，教学过程中，注重帮助学生积累基本活动经验，就能推动学生思考数学问题，发展数学核心素养。