人教A版高中数学实验教科书与高中数学教科书的比较研究

逯彦周 项丽红

[摘要]对人教A版2007版高中数学实验教科书与2019版高中数学教科书中“函数单调性”内容从课标要求、概念引入、概念表述、概念理解、概念运用方面进行比较，并对教师教学提出一些建议，

[关键词]函数单调性;教材比较;概念

“函数单调性”是学生在高中阶段学习的第一个函数基本性质，其研究方法对后续函数性质的学习具有示范引领作用：是学生第一次经历用数学符号语言表达数学概念，从而体会数学的简洁美：并且单调性概念的形成过程体现了数学概念逐步抽象的过程，是培养学生数学抽象素养的绝佳素材，因此，有必要对不同教材中的“函数单调性”内容加以比较，并对教师教学提出相应建议。

1研究对象

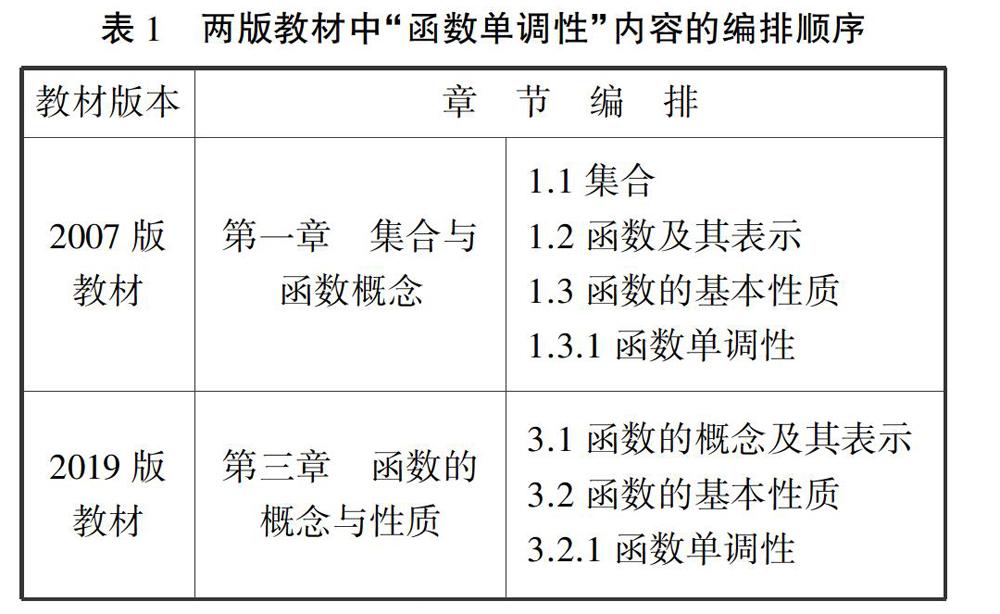
研究对象为依据《普通高中数学课程标准（实验）》（以下简称03版课标）编写的2007年第2版《普通高中课程标准实验教科书数学1必修（A版）》（以下簡称2007版教材）与依据《普通高中数学课程标准（2017年版）》（以下简称17版课标）编写的2019年第1版《普通高中教科书数学必修第一册（A版）》（以下简称2019版教材）中的“函数单调性”内容，本内容在两版教材中的所处位置见表1。

2007版教材的编排顺序为：1.1集合→1.2函数及其表示→1.3函数的基本性质（第1课时：函数单调性），2019版教材的编排顺序为：第一章集合与常用逻辑用语→第二章一元二次函数、方程和不等式→第三章3.1函数的概念及其表示→3.2函数的基本性质（第1课时：函数单调性）。

2研究结果

2.1课标要求

2003版课标对“函数单调性”的要求是“通过已学过的函数特别是二次函数，理解函数的单调性：学会运用函数图象理解和研究函数的单调性，”2017版课标对“函数单调性”的要求是“借助函数图象，会用符号语言表达函数的单调性，理解其作用和实际意义。”

2.2概念引入

2007版教材“函数单调性”概念引入遵循“三部曲”：图形语言→自然语言→符号语言，即先从学生熟知的一次函数，f（x）=x和二次函数f（x）=x²的图象人手，观察获得图象“上升”“下降”的直观感知，再取值填表得到“函数值随着自变量的增大而增大或减小”的自然语言描述，最后用数学符号语言刻画这种规律。

2019版教材“函数单调性”概念引入也遵循“三部曲”：首先，开门见山“在初中，我们利用函数图象研究过函数值随自变量的增大而增大（或减小）的性质，这一性质叫做函数的单调性”：接着以二次函数f（x）=x²为例，先从图象可看到：图象在y轴左侧从左到右下降，即当x

2.3概念表述

3结论与建议

3.1研究结论

3.1.1两版教材概念引入、概念表述基本一致，概念理解2019版教材更详细

两版教材概念引入基本一致，均采用“三部曲”完成，即图形语言→自然语言→符号语言，但在得出自然语言时，2019版教材没有通过取值填表得到，而是直接叙述“当x

3.1.2概念运用上，2007版教材更注重数形结合，2019版教材更注重概念的形式化运用

两版课标对“函数单调性”要求不同，两版教材编写遵循课标要求从前面的分析可以看出，两版教材相比较：2007版教材在例题、习题上更加注重数形结合，题目多为在函数图象基础上研究函数单调性，这类题目在例题中占50%，练习题中占75%，习题中占40%;2019版教材在例题、习题安排上更加注重数学概念的形式化运用，题目多为证明函数单调性，这类题目在例题中占100%，练习题中占75%，习题中占30%。

3.1.3两版教材相比，2019版教材例习题更注重分类讨论，且难度增加

3.2教学建议

3.2.1可采用概念形成与概念同化相结合的概念获得方式

概念的获得包括概念形成与概念同化两种，概念形成指从大量同类事物的不同例证中独立发现：概念形成指利用已有认知结构中的有关知识来理解新概念，因此，可先通过具体的典型实例，如f（x）=x、f（x）=x²引导学生概括发现“y随x的增大而增大或减小”性质而形成“函数单调性”定义，并用符号语言加以刻画，揭示定义后，再引导学生在定义指导下去观察已学过的一般一次函数、二次函数、反比例的单调性，进一步加深概念理解。

3.2.2恰当使用反例帮助学生理解“函数单调性”概念

反例提供了最有利于辨别的信息，对概念的深化具有重要作用，恰当使用反例可使学生对概念的理解更加精确，“函数的单调性”概念中“D∈I、“任意”都会因学生理解不全面而产生错误，因此需要呈现反例来加强理解，如2019版教材设置的“思考”可起到这样的作用，

3.2.3逐步促进学生数学抽象、逻辑推理、数学运算素养达成

学生数学核心素养的形成不是一蹴而就的，需要教师在日常教学中加以落实，“函数单调性”内容，重点要培养学生的数学抽象、逻辑推理、数学运算素养，在概念形成中，学生经历了由具体到抽象，由图形语言和自然语言到符号语言表达的过程，发展了数学抽象素养在表述“函数单调性”概念以及用定义证明函数单调性的过程中，体会全称量词、存在量词等逻辑用语的作用，发展了逻辑推理及数学运算素养。