基于改进萤火虫算法的多阈值微生物图像分割

武 治，孙照旋，周 芳

(安徽工业大学电气与信息工程学院，安徽马鞍山243032)

随着城市化进程的不断加快以及居民消费、生活水平的不断提高，如何处理大量的工业、生活污水成为亟待解决的问题。利用显微成像获得污水中微生物图像，并通过图像处理技术提取感兴趣区域来分析它们的种群结构特征，以此开发高效的污水处理系统是目前研究的热点[1]。其中如何提高图像特征提取的质量是一个基础而又重要的步骤。图像分割技术自1970年问世以来，有成千上万种算法被提出，但是没有一种算法能够在不修改的情况下应用于所有场景。因此，针对特定应用场景开发一种高效的图像分割算法十分必要。目前图像分割算法依据算法原理可以分为基于阈值的分割算法[2]、基于边界的分割算法[3]、基于区域的分割算法[4]、基于纹理的分割算法[5]等。其中基于阈值的分割算法由于其简便、高效的特点而得到广泛应用。阈值分割包括单阈值分割与多阈值分割，在图像背景信息复杂的情况下，单阈值分割往往达不到良好的分割效果，多阈值分割可在图像中设置多个阈值，提高分割的准确性。多阈值算法能够达到很好的分割效果，但是传统最大熵多阈值分割算法常用穷举法求解，算法的时间复杂度较高。在此背景下，结合群智能算法的迭代寻优方法被广泛应用于多阈值分割。Liang 等[6]设计了一种蚁群优化分割算法来解决多级最大类间方差问题；Sathya等[7]采用细菌觅食算法寻找能使目标函数达到最大的阈值。然而，随着阈值数目的增加，这些元启发式优化算法无法找到全局搜索和局部搜索之间的平衡，导致寻优结果的不准确和收敛速度的缓慢。

萤火虫算法由剑桥大学的Yang[8]提出，相较于其他智能优化算法，萤火虫算法每只萤火虫个体都拥有自己的动态决策范围，只依赖局部的相关信息进行搜索，最终将整个萤火虫群体分为单独的多个子群体，收敛于多个局部最优解或全局最优解。许多学者在不同领域应用萤火虫算法并进行相关改进，成功解决了功能优化问题。但是目前改进型萤火虫算法的共同问题是当算法接近最优解时，在最优解附近来回振荡，影响运算速度和最终结果。因此，文中提出一种新的改进萤火虫算法，在初始化阶段通过对称变换矩阵来提高萤火虫与最优解之间的相关性，调整变量参数使萤火虫个体能够准确、快速地收敛于最优解，并将图像信息熵作为目标函数，采用改进的萤火虫算法搜索使微生物图像具有最大熵的全局最佳阈值。在本文提出的算法中，熵与每个萤火虫的亮度有关。

1 多阈值个数的自动获取

为准确确定微生物图像多阈值分割所需的阈值数目m，降低直方图中伪波峰错分为波峰从而对分割结果造成的影响，文中从分析灰度直方图出发，提出一种自动确定图像阈值数目的算法。假设微生物灰度图像的灰度级数目为L，灰度值为i∈[0,L-1]，灰度直方图为h，频数的平均值have=mean(h)。算法的主要流程如下：

1)输入微生物图像，对彩色微生物图像进行灰度处理，统计出灰度直方图；

2)依据统计出的灰度直方图，依次对灰度值对应的频数进行对比，若某个灰度值的频数大于其左右相邻灰度值的频数，则将对应该灰度值的频数为一个波峰；

3)第2)步统计出的波峰包含伪波峰，为避免伪波峰错误地分为波峰，设置波峰间的距离为D，将距离D前后范围内出现的波峰均看作一个波峰；

4)图像中存在的多个目标会占据图像中的多数像素点，为了进一步准确定位波峰，取灰度值大于have的波峰；

5)令灰度值i的频数为波峰Ci，波峰个数Cn的计算公式为

6)依据步骤5)的结果，确定分割所需的阈值数目m=Cn-1。

2 萤火虫算法的基本原理

2.1 萤火虫算法的数学表述

根据萤火虫算法的仿生原理，萤火虫算法的数学描述如下，萤火虫个体的相对发光强度可由式(2)确定

式中：rij为萤火虫i和j之间的空间欧几里得距离；I0为rij=0 时萤火虫的发光强度，即原始发光强度，与目标函数成正比；γ为亮度衰减参数，这意味着在特定的传播介质中亮度将会衰减。

萤火虫之间的相对吸引力由式(3)得出

其中β0为两只萤火虫之间的距离为零时的相互吸引力，也是两者之间的最大吸引力数值。萤火虫i依据式(4)向比其更亮的萤火虫j移动，

原始萤火虫算法的缺点是两只萤火虫之间的信息交换受到其搜索范围的影响，萤火虫初始化的位置是随机分配的，并且萤火虫之间的独立性较大，没有相互关联；萤火虫设置的荧光素值过于离散，以致无法相对较慢地运行；其次，在萤火虫算法中，控制搜索范围的参数是随机设置的，仿真结果也是随机的。为解决萤火虫算法目前存在的问题，文中对算法进一步的改进。

2.2 改进的萤火虫算法

2.2.1 对称矩阵变换

原始萤火虫算法需在萤火虫个体运行之前随机设置初始位置，导致两只萤火虫个体之间的相关性降低，容易陷入局部最优解。为此提出一种参数初始化方法，通过对称变换矩阵计算得到初始设置的随机萤火虫位置，如式(5)所示[9]

式中：λ的取值范围是(0，1)；xk1和xk2由相应的xi和xj计算得出，作为萤火虫算法的初始参数。通过对称矩阵变换得出的萤火虫个体之间具有较强的相关性，从而提高了萤火虫算法的运行效率与寻优结果的准确性。

2.2.2 变量参数的调整

为进一步提高算法的准确性，运用步长量化因子α和相对吸引力参数βij改进不同区域萤火虫运动的影响占比。在单只萤火虫因子的邻域，亮度的衰减对萤火虫运动的影响较大，βij占主导地位，从式(2)可看出，βij与萤火虫亮度的衰减有关。在原始萤火虫算法中，亮度衰减参数λ通常设置为1，而且在特定的传播介质中亮度衰减会随着距离而变化，文中采用式(6)[9]调整参数γ。

两只萤火虫之间的相对吸引力式(3)也相应调整为

萤火虫个体的移动在受到亮度衰减影响的同时，也受到各萤火虫之间相互吸引度的影响。这时，算法的迭代速度将占据主导地位。萤火虫算法通过式(4)的参数α设定步长，用来控制两只萤火虫个体之间的移动速度，从而控制迭代速度。随着迭代次数不断增加，所有萤火虫个体逐渐接近最优解位置，搜索范围也逐渐减小。因此，考虑将参数α设置为线性递减函数，从而更好地控制迭代速度。改进的公式如(8)

式中：αmax为初始设置的最大量化步长；αmin为最小量化步长；Tmax为初始设置的最大迭代次数。

3 基于改进萤火虫算法的多阈值分割

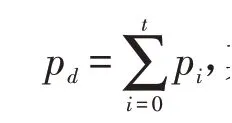
Hd(t)和Hb(t)分别代表目标区域和背景区域的熵值，可由下式表示：

图像的总熵值可以表示为

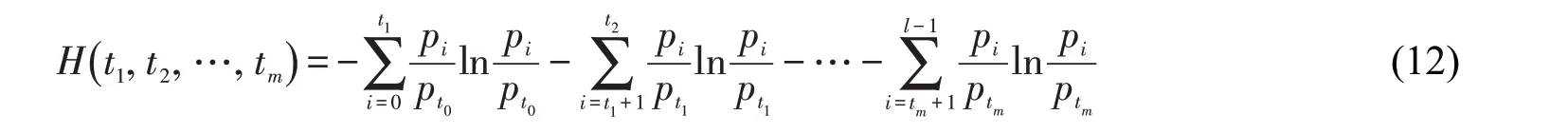
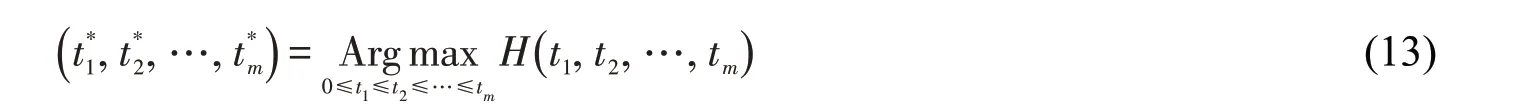
基于改进萤火虫算法的多阈值分割实现步骤如下：

1)输入微生物图像，依据式(1)确定寻优过程的具体阈值数目m；

2)依据式(6)，(8)初始化参数，包括萤火虫种群数量S、最大吸引度β0、亮度衰减参数γ、步长α和最大迭代次数Tmax；

3)将式(12)作为目标函数，随机初始化位于搜索范围内的萤火虫i的位置xi，依据目标函数计算每只萤火虫的亮度I0；

4)依据式(2)和(7)计算萤火虫i的相关亮度I以及相关吸引度β，萤火虫i的移动方向也由相关吸引度确定；

5)将式(6)和(7)分别代入式(4)，更新每只萤火虫的位置，获得当前最优位置xi(t+1)和当前相对亮度I；

6)迭代执行步骤4)和5)，直到达到预先设定的最大迭代次数，输出最优目标函数值H(t1,t2,…,tm)max和最优解

7)根据输出的最优解对微生物图像进行多阈值分割，输出微生物多阈值分割图像。

算法流程图如图1。

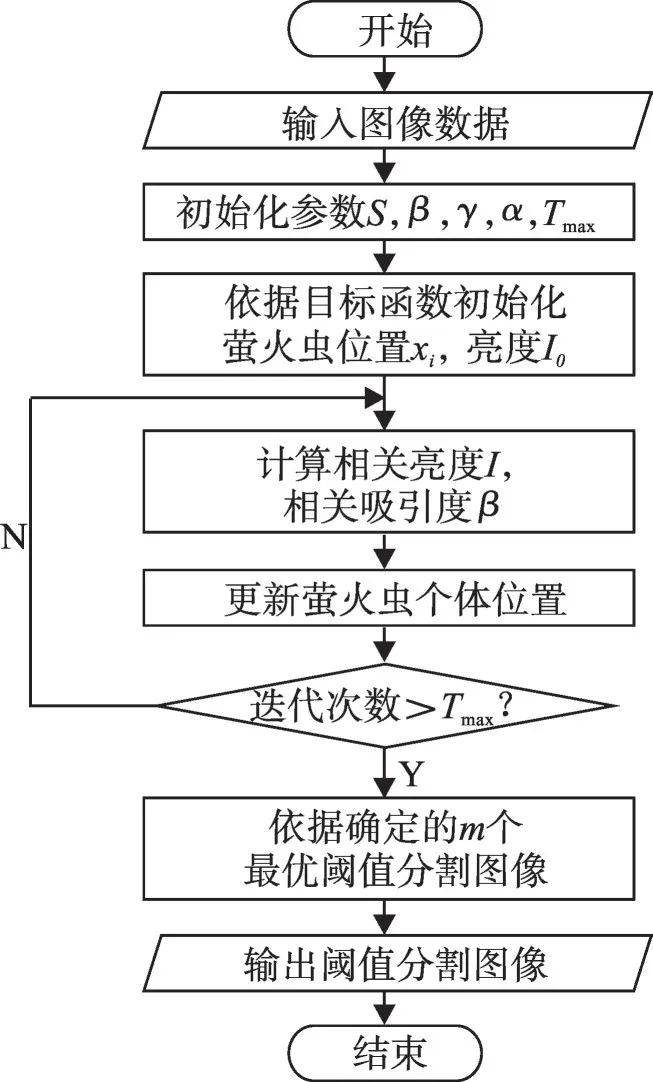
图1 改进萤火虫多阈值分割算法流程图Fig.1 Flow chart of improved firefly multi-threshold segmentation algorithm

4 实验与结果分析

为验证本文改进的萤火虫多阈值分割算法的准确性与时效性，采用该算法进行微生物图像分割实验。图像选自污水处理指示性微生物图谱[10]，图像分辨率大小为250× 250；实验操作环境为MATLAB2017a；测试电脑配置为windows10，64 位操作系统，8 GB运行内存。设置萤火虫种群数目S=50，Tmax=100，初始步长αmax=0.5，αmin=0.2，β0=1 表示两只萤火虫之间的距离为0时的相互吸引力。

4.1 量化指标

在图像质量的统计分布差异指标测量中，文中选择标准化绝对误差(NAE)、均方根误差(MSE)、峰值信噪比(PSNR)[11]3个指标评测改进的萤火虫多阈值分割算法的准确性，同时通过CPU占用的运行时间评测算法的时效性。NAE，MSE，PSNR通过如下公式计算得到。

式中：rNAE，rMSE，rPSNR分别表示标准化绝对误差，均方根误差和峰值信噪比；M表示图像列数：N表示图像行数；j，k为图像中的像素坐标，表示分割之前的原始图像和分割之后图像的像素。

4.2 基于改进萤火虫算法的多阈值分割实验结果分析

本实验采用的微生物图像如图2，以最大熵作为萤火虫算法的目标函数，分别对每个标准微生物图像进行直方图统计，实验结果如图3。根据式(1)和直方图统计结果确定的4幅图像分割阈值数目分别为3，4，2，5。为对比本文提出的算法，选择一维熵[12]、二维熵[13]、最大类间方差[14]、基于粒子群的多阈值分割算法[15]及原始萤火虫算法进行比较。对应各算法的量化指标如表1。实验结果以二值图像的形式呈现，如图4。

图2 微生物图像Fig.2 Microbiological images

表1 各算法分割质量评估数据Tab.1 Segmentation quality evaluation data of each algorithm

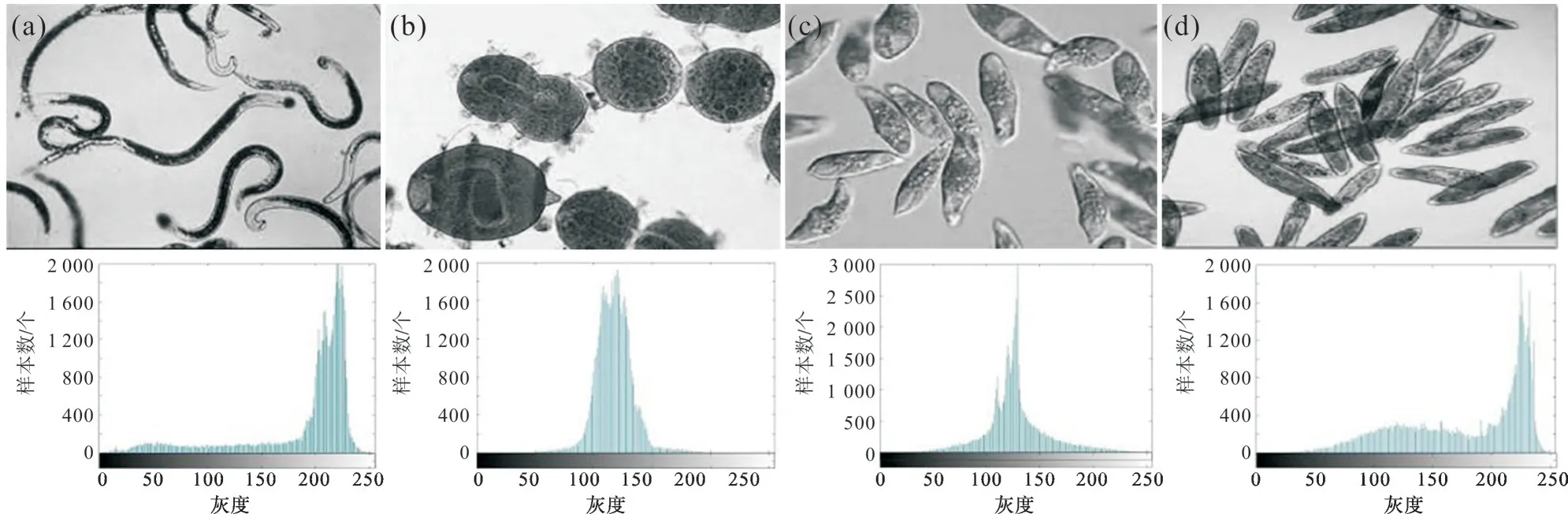
图3 灰度微生物图像以及直方图统计Fig.3 Gray-scale microbial image and histogram statistics

由图4可看出，一维熵、二维熵、Otsu 3种算法分割出的微生物存在边缘轮廓残缺、目标不完整等问题，严重影响分割的准确性及后续处理过程，而基于群智能优化算法的多阈值分割根据灰度直方图设置了多个分割阈值，分割效果明显改善。粒子群和原始萤火虫多阈值分割算法仍然存在目标不完整问题，相比较于以上5种算法，本文改进萤火虫算法在边缘轮廓残缺度以及前景完整度上都有改善。同时根据表1量化指标，一维熵、二维熵、Otsu 3种算法的NAE、MSE均较高且PSNR 不高，群智能优化算法相比较于以上3种算法取得显著改善，本文改进算法3项指标在多阈值分割算法基础上得到了进一步优化，图像分割准确性增加。在占用CPU 运行时间上，因为单阈值分割只需确定一个数值作为分割阈值，因此时间较短，但是分割准确性不高，在兼顾准确性与时效性的前提下，改进萤火虫算法由于在初始化阶段提高了萤火虫个体的相关性，并且通过调整参数控制算法的迭代速度，降低了CPU运行时间。

图4 各算法微生物图像分割结果Fig.4 Microbiological image segmentation result of each algorithm

5 结 论

提出一种结合改进萤火虫优化的多阈值微生物图像分割算法，使用萤火虫智能算法迭代寻找分割图像的多个阈值，从而使目标函数总熵值达到最大。实验结果显示，该算法在目标分割准确性和效率上相较于原始萤火虫算法和其他阈值分割算法都有明显提高。但是在目标严重粘连区域，算法仍然存在分割不完整、边缘轮廓不清晰等问题，需要在未来的工作中进一步改进。