空心和实心车轴微动磨损行为的对比研究

陈 刚，曾东方，张 艳，鲁连涛，宫昱滨，张关震

(1.宝武集团马钢轨交材料科技有限公司轨道交通关键零部件先进制造技术国家地方联合工程研究中心，安徽马鞍山243000；2.西南交通大学牵引动力国家重点实验室，四川成都610031；3.中国铁道科学研究院集团有限公司金属及化学研究所，北京100010)

铁路车轴在服役过程中承受周期性的旋转弯曲载荷，导致车轴和轮毂配合边缘出现微动现象[1-2]。由此现象引起的微动磨损和微动疲劳将缩短车轴服役寿命，威胁列车的运行安全[3]。随着列车高速化和轻量化发展需求的日趋迫切，高速列车广泛采用空心车轴轮对技术，但目前尚未颁布空心车轴的相关设计标准。实际运用中，空心与实心车轴仍采用相同的设计参数，如过盈量、轮毂凸悬量等。某铁路机车厂检修时发现，空心车轴轮座边缘相对实心车轴磨损更为严重，严重的微动磨损导致车轴过早报废。空心和实心车轴的刚度存在差异，在相同过盈量下，二者配合面的微动参量有所不同，致使空心车轴磨损严重。因此，有必要研究空心与实心车轴微动磨损行为的共性和差异。

轮轴配合面的微动损伤主要由接触压应力、摩擦剪切应力和滑移幅值等3个微动参量控制[4]。由于轮轴是通过过盈配合联结而成的封闭结构，难以通过试验方法直接测量上述3个微动参量。因此，有限元分析被广泛用于研究过盈配合结构的微动行为。如杨广雪等[5]、曾飞等[6]、冯垣洁[7]应用有限元计算获得了轮轴配合面上的微动参量分布，并对轮轴微动磨损程度和微动裂纹萌生行为进行了分析；曹志礼等[8]、黄洁[9]仿真分析了空心轴过盈配合面的应力分布；平学成等[10]仿真分析了空心轴配合面的接触压应力分布，并评估了车轴微动损伤情况。上述仿真手段未考虑过盈配合面微动磨损引起的微动参量的变化。实际上，微动磨损会导致过盈配合面的轮廓发生变化，进而影响微动参量。要获取接近实际情况的轮轴配合面微动损伤参量必须考虑微动磨损。张远彬等[11-12]建立了基于Achard磨损模型的过盈配合结构微动磨损仿真模型，研究了微动磨损对过盈配合面微动参量的影响，并基于多轴疲劳理论建立了过盈配合结构的微动疲劳预测模型。在上述研究的基础上，曾东方等[13]分析了卸荷槽尺寸对铁路车轴过盈配合部位微动行为的影响。本文以轮轴结构为研究对象，在考虑车轴微动磨损的基础上分析磨损轮廓随微动循环周次的演化，对比研究空心与实心车轴微动磨损和微动参量的共性与差异。

1 有限元分析方法

1.1 有限元模型

根据某铁路机车轮轴尺寸，应用有限元前处理软件HYPERMESH建立图1所示模型。轮座和轴身直径分别为252，230 mm，卸荷槽半径和深度分别为16，1 mm。本研究中，空心车轴的内径为138 mm，对应于标准规定的空心车轴内外径之比的上限0.6[14]。轮轴间过盈量设定为210 μm，约为轮座直径的0.083%，接近标准规定的下限[15]。有限元单元类型采用八节点六面体完全积分单元C3D8。轮对配合边缘部位的最小网格尺寸细化为200 μm，见图1(b)。轮座和车轮接触面间的库仑摩擦系数设置为0.6，切向接触行为采用罚函数接触算法进行模拟。考虑到轮轴接触会导致应力集中，采用双线性弹塑性随动强化模型模拟材料行为，车轴和车轮材料力学性能参数见表1。

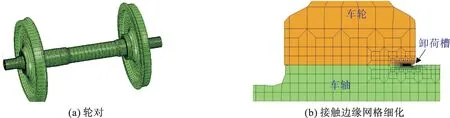
图1 轮对有限元模型Fig.1 Finite element model of wheel set

表1 材料力学性能Tab.1 Mechanical properties of materials

车轴在制动工况时受力条件最恶劣，因此文中有限元仿真采用制动工况。仿真参数如下：轴重Q为25 000 kg，单轴一系簧上质量m1为19 700 kg，单轴一系簧下质量m2为5 300 kg，单轴箱组成质量m3为90 kg(左)、180 kg(右)，从动齿轮质量m4为471 kg，齿轮箱质量(含齿轮)m5为300 kg，闸瓦压力Ff为25 000 N，车轮滚动圆半径R为625 mm，左右轴颈载荷中心线间距离2b为2 050 mm，车轮滚动圆间距离2s为1 493 mm，制动摩擦系数Γ为0.35，制动半径R1为448 mm。模型受力和边界条件见图2。图2中，FfΓ，0.3PR和FfΓR1/R分别是制动工况下x，y，z方向的附加力矩。根据TB/T 2395—2008，计算制动工况下的车轴受力：

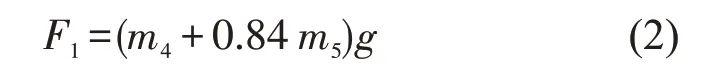
式中：P1和P2为作用于车轴轴颈的垂向力；F1为未安装在弹簧上的部件所施加的力。有限元仿真中轮对的滚动通过以上载荷在垂直于车轴的平面上旋转来模拟，应用ABAQUS 中的重启动分析(Restart)功能实现载荷的不断循环。

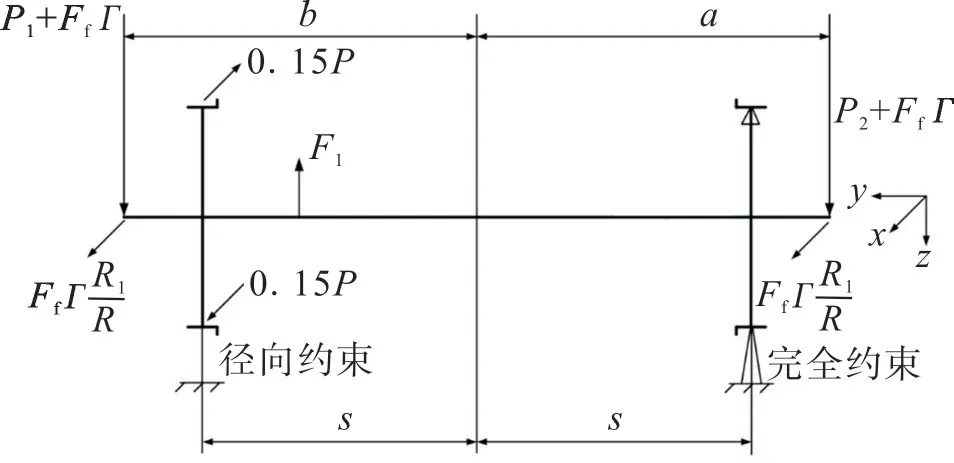
图2 轮对有限元模型上的受力及边界条件Fig.2 Forcesand boundary conditions on FEmodelof wheelset

1.2 微动磨损的计算模型

Archard 磨损方程适用于有限元计算的修正，公式为

式(3)表示节点x在时间t的磨损深度Δh(x,t)与接触压应力Δp(x,t)和滑移距离ΔS(x,t)的关系。为加速计算，采用循环周次跳跃技术，即假设ΔN个循环内磨损速率保持不变。基于此，Archard磨损方程修正式为

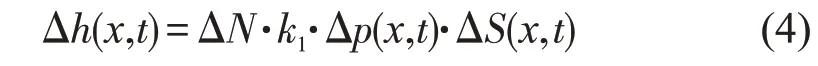
文中仿真计算所用局部磨损系数k1=2×10-8，循环跳跃次数ΔN=10 000。

有限元微动磨损计算流程见图3。在ΔN次循环的磨损作用下，轮轴配合面磨损区节点沿法向移动，移动距离可根据式(4)计算得到，并通过FORTRAN 语言编写的ABAQUS 子程序UMESHMOTION实现。为避免磨损区的网格畸形，采用ALE 自适应网格技术，对磨损区网格进行自适应平滑处理，见图4。

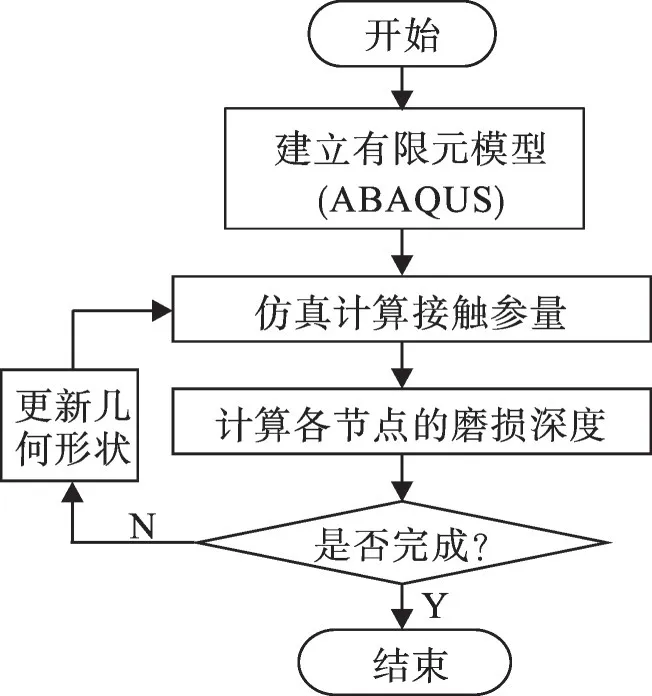
图3 微动磨损计算流程图Fig.3 Flow chart of fretting wear calculation

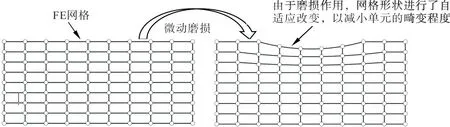
图4 有限元模型的几何形状更新示意图Fig.4 Schematic diagram of geometry updating of FE model

2 结果与讨论

2.1 微动磨损轮廓

空心与实心车轴磨损深度随微动循环周次的演化如图5，图中186 mm位置为轮轴接触边缘。由图5可看出：空心和实心车轴的微动磨损都发生在轮轴接触边缘附近的区域，且磨损深度和宽度都呈逐渐增加的趋势。空心与实心车轴磨损轮廓如图6。由图6可见：空心和实心车轴的最大磨损深度均出现在接触边缘，距离接触边缘越远，微动磨损越小；循环周次为1 250 000时，空心和实心车轴的最大磨损深度分别为0.005 5，0.004 7 mm，空心车轴的磨损程度大于实心车轴。

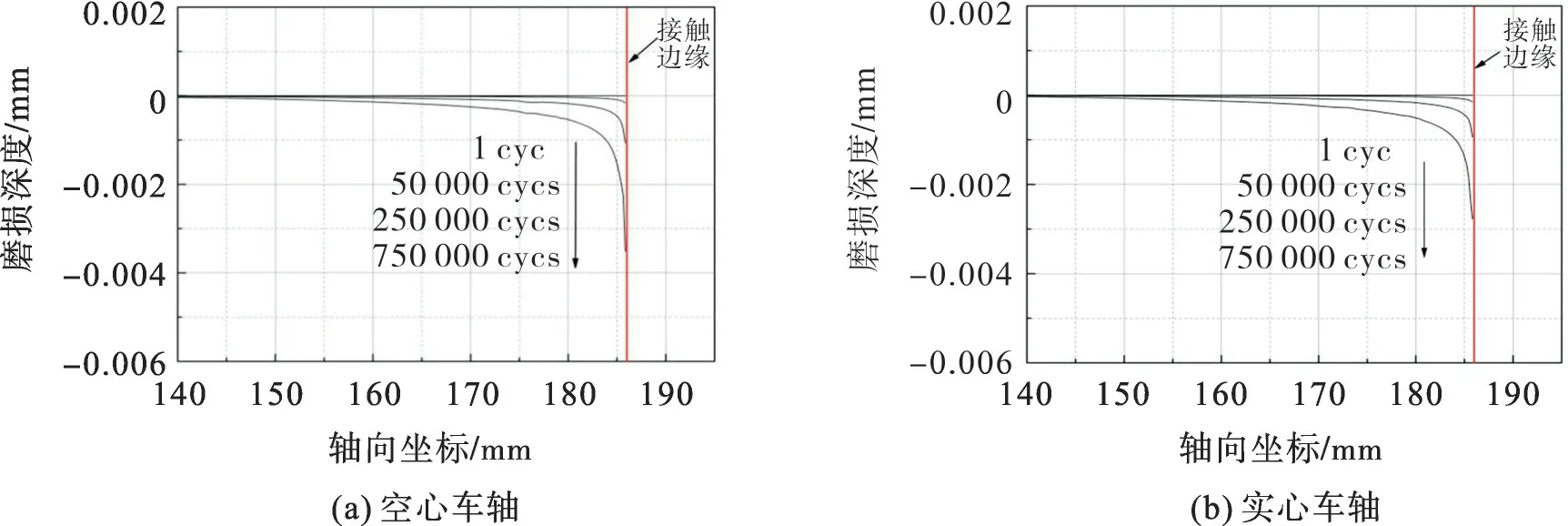
图5 磨损深度随循环周次的演化Fig.5 Evolution of fretting wear with fretting cycles

2.2 接触压应力

由于微动损伤更易发生在车轴的受拉侧，因此对受拉状态的车轴进行研究。车轴轮座接触压应力随微动循环周次的演化如图7。由图7(a)可见：文中施加载荷的作用下，车轴的接触压应力均大于0，受拉侧没有出现张开区；50 000循环周次以内，空心车轴轮座边缘由于边缘效应发生了应力集中；循环超过50 000 周次时，在微动磨损的作用下，材料的移除缓解了空心车轴轮座边缘的应力集中程度，由于微动磨损导致的几何不连续，新的应力集中位于磨损与未磨损的过渡区域；磨损区域随循环周次的增加而增加，导致应力集中远离轮轴配合边缘。

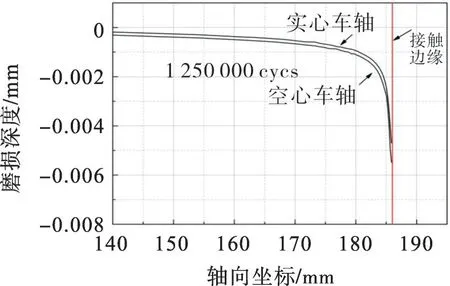
图6 空心与实心车轴的磨损轮廓Fig.6 Wear profiles of hollow and solid axles

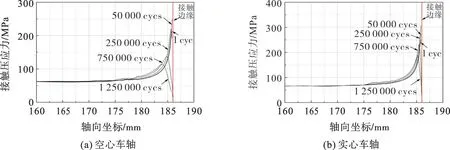
图7 接触压应力分布及变化情况Fig.7 Distribution and change of contact pressure stress

由图7(b)可见，实心车轴与空心车轴的配合面接触压应力变化规律相似，但实心车轴应力集中在250 000微动循环周次后才开始远离接触边缘。

图8 为1250 000 周次的微动循环后，空心与实心车轴配合面的接触压应力分布。由图8 可见：在配合面中心位置，空心车轴的接触压应力略小于实心车轴，这是因为空心车轴更易向内部发生弹性变形；在配合边缘，空心车轴的应力集中程度也明显小于实心车轴，这是由于空心车轴地微动磨损更严重，磨损对应力集中的缓解作用也更明显；空心和实心车轴的接触压应力峰值分别为106，188 MPa。

2.3 摩擦剪切应力

空心和实心车轴受拉侧轴向摩擦剪切应力分布及其随循环周次的演化如图9。由图9可见，摩擦剪切应力与接触压应力的分布和变化规律相似。

图10为1250 000周次的微动循环后，空心与实心车轴摩擦剪切应力分布。由图10可见：在配合边缘处，空心车轴的摩擦剪应力较实心车轴小；两类车轴的应力峰值也不同，空心车轴的应力峰值位置较实心车轴更靠近配合区内部。

空心和实心车轴过盈配合面摩擦剪切应力及其分布分别如图11，12。图中虚线为临界摩擦剪切应力。摩擦剪切应力小于临界值，则相应位置处于粘着状态；等于临界值，则相应位置处于滑移状态。由图11，12 可见：在250 000 循环周次以内，空心和实心车轴的整个接触区域均处于粘着状态；随后滑移区出现并逐渐增加，当循环周次增加至1 250 000，空心车轴的粘-滑交界移到184.11 mm，实心车轴的粘-滑交界移到185.38 mm。显然，空心车轴的滑移区较实心车轴大。

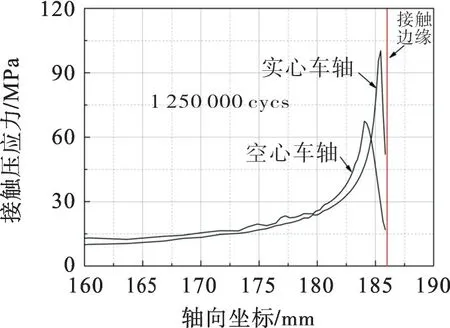
图10 空心与实心车轴的摩擦剪切应力分布Fig.10 Distribution of friction shear stress of hollow and solid axles

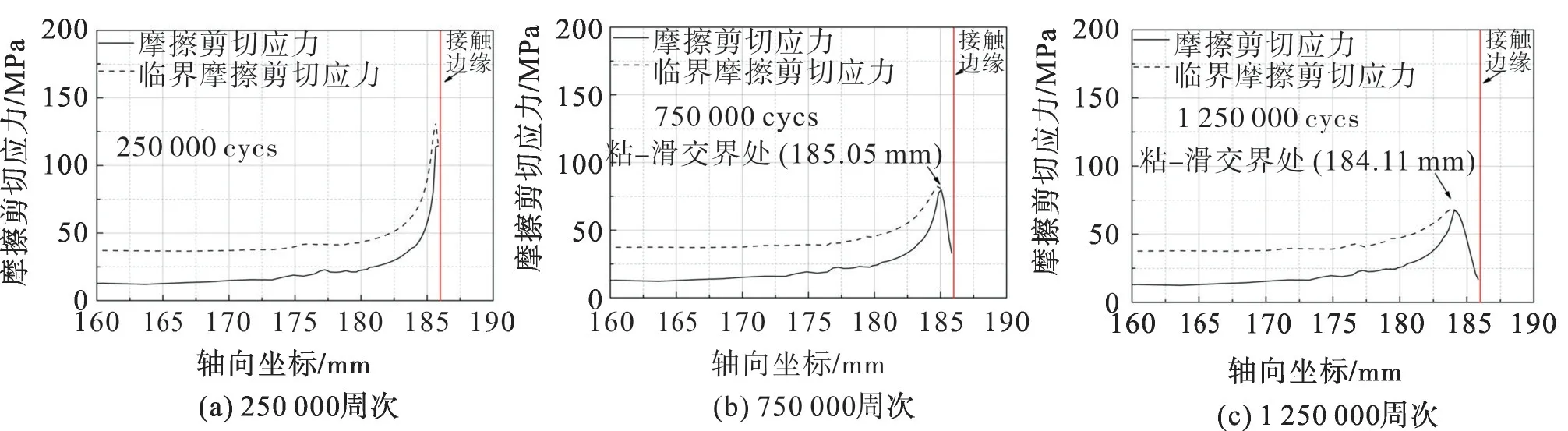
图11 空心车轴摩擦剪切应力与临界摩擦剪切应力的分布Fig.11 Distribution of friction shear stress and critical friction shear stress of hollow axle

图12 实心车轴摩擦剪切应力与临界摩擦剪切应力的分布Fig.12 Distribution of friction shear stress and critical friction shear stress of solid axle

2.4 滑移幅值

车轴过盈配合面滑移幅值分布及其随微动循环周次的演化如图13。由图13可见，空心和实心车轴配合面滑移幅值分布及演化具有相似规律，最大滑移幅值均出现在配合面的接触边缘位置。由图5可知，严重的微动磨损发生在接触边缘，减小了该位置的接触压应力和摩擦剪切应力，进而导致滑移幅值增加。微动循环周次达到1250 000时，空心与实心车轴滑移幅值如图14。由图14可见：空心车轴的滑移幅值较实心车轴的滑移幅值大，约为实心车轴的2倍；空心和实心车轴的滑移幅值峰值分别约为0.00 193，0.001 mm。

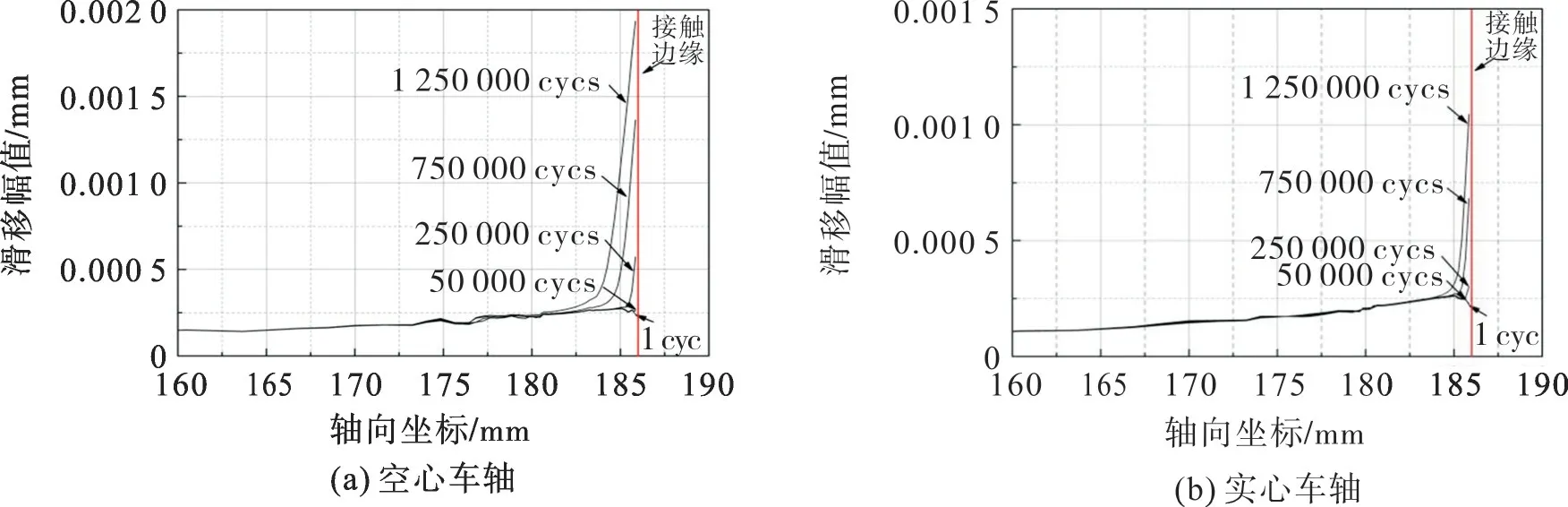
图13 轴向滑移幅值分布及变化情况Fig.13 Distribution and variation of axial slip amplitude

根据Archard 磨损方程，磨损深度随接触压应力和滑移幅值的增加而增加。通过上述分析可知，在车轴外形尺寸和载荷工况相同的情况下，空心车轴配合面滑移幅值较大而接触压应力较小。故认为较大的滑移幅值是导致空心车轮轴微动磨损大于实心车轴的主要原因。

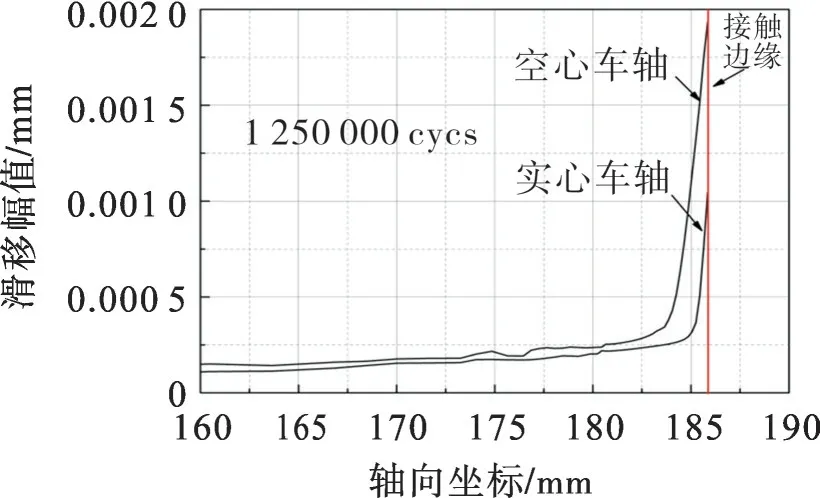
图14 空心与实心车轴的滑移幅值分布Fig.14 Distribution of axial slip amplitude of solid and hollow axles

3 结 论

1)车轴配合边缘的应力集中程度由于微动磨损而缓解，新的应力集中位于磨损与未磨损的过渡区域。磨损区域随着循环周次的增加而增加，导致应力集中远离轮轴配合边缘。

2)空心车轴具有更严重的微动磨损，对应力集中的缓解作用较显著，从而导致空心车轴的应力集中程度明显小于实心车轴。

3)在靠近过盈配合边缘的区域，空心车轴的滑移幅值大于实心车轴，导致空心车轴过盈配合区域的微动磨损大于实心车轴。