发电锅炉燃烧过程Smith预估解耦控制策略
胡 欢
(上海宝山钢铁股份有限公司能源环保部,上海200941)
锅炉燃烧控制系统是火力发电厂单元机组的主要控制系统之一,对于锅炉的安全高效运行和节能降耗具有重要意义[1-2]。发电锅炉燃烧系统具有非线性、强耦合和大滞后等特点,控制难度大,故对锅炉燃烧系统进行有效控制已成为火力发电领域的一项重要研究课题[3]。实际工程应用中,往往采用常规PID策略对发电锅炉燃烧过程进行控制,但无法彻底消除各回路之间的耦合现象,难以达到理想的控制效果。已有学者将预测控制、神经网络控制以及改进的PID控制等先进控制理论应用到锅炉燃烧控制系统中,如冯冬青等[4]采用神经网络建立锅炉燃烧系统模型对锅炉燃烧系统进行控制,改善了系统的抗干扰性能,但只是针对燃烧系统中主蒸汽压力这一子系统,没有全面考虑整个燃烧系统的控制优化;代自慧等[5]提出锅炉模糊PID控制方案对锅炉燃烧系统进行控制,仿真结果表明控制效果较理想,但实际应用中难以达到预期的控制效果;阮琦等[6]将改进蚁群PID-神经元解耦控制策略应用到锅炉主蒸汽压力控制中,仿真结果表明,当系统出现较大的非线性时难以达到预期的控制效果。综上所述,对锅炉燃烧系统进行解耦优化控制仍存在不足。为此,本文基于Smith预估补偿器与解耦控制算法,提出一种锅炉燃烧优化控制策略,将锅炉燃烧控制系统简化为一个双输入、双输出控制系统,并对输入输出对象进行解耦,再使用Smith预估补偿器对控制系统中存在的滞后环节进行补偿,优化控制效果。
1 Smith预估解耦控制策略
主蒸汽压力和排烟氧量是燃煤发电锅炉控制系统的两个重要被控参数,主蒸汽压力是反映锅炉燃烧工况的关键参数,排烟氧量是锅炉经济运行的重要指标。根据燃煤锅炉燃烧控制系统的需求,文中以喷煤量和送风量为输入量,利用不变性解耦原理的控制方法将系统的主蒸汽压力和排烟氧量两个相互耦合的控制回路解耦为两个相互独立的子系统,然后分别使用两个PID控制器组成串级回路对解耦后的两个独立子系统进行控制,并使用Smith预估补偿器进行补偿,以改善滞后补偿控制效果。燃烧控制系统框图如图1。
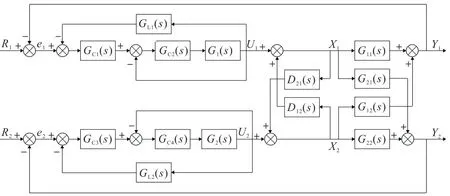
图1 燃烧系统Smith预估解耦控制框图Fig.1 Smith predictive decoupling control block diagram of combustion system
图1 中GC1(s),GC2(s),GC3(s),GC4(s)分别为主蒸汽压力、燃料流量、排烟氧量以及送风量控制器,均使用PID控制器;G1(s)为燃料流量对象的传递函数;G2(s)为送风量对象的传递函数;G11(s),G21(s),G12(s),G22(s)分别为燃料流量和送风量到主蒸汽压力和排烟氧量的传递函数;D12(s),D21(s)为组成解耦器;GL1(s),GL2(s)为Smith预估补偿器;R1为给定主蒸汽压力;R2为给定排烟氧量;e1为主蒸汽压力给定值与实际值偏差;e2为排烟氧量给定值与实际值偏差;U1为主蒸汽压力控制器输出值;U2为排烟氧量控制器输出值;X1为燃料流量输出值;X2为送风量输出值;Y1为主蒸汽压力实际值;Y2为排烟氧量实际值。
1.1 不变性解耦原理
以双输入双输出系统为例[7-8],其控制原理框图如图2。由图2可知,系统内控制通道传递函数为G11(s)和G22(s),耦合通道传递函数为G12(s)和G21(s),D12(s)和D21(s)为解耦支路。
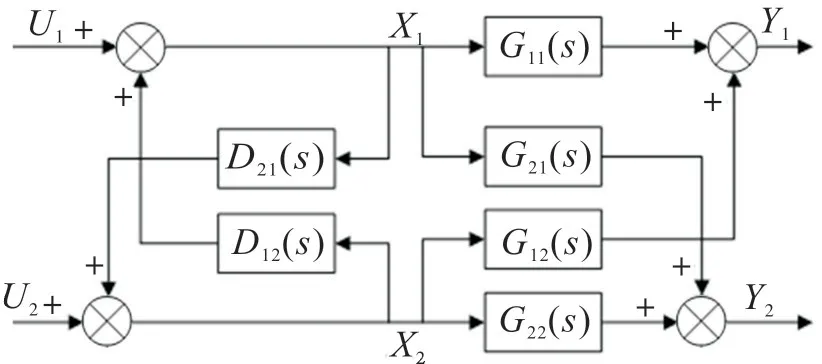
图2 不变性原理解耦控制框图Fig.2 Decoupling control block diagram of invariance principle
输出Y为:
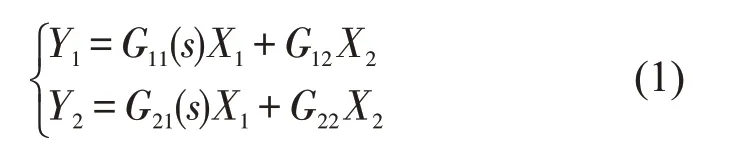
记作

由图2可知:
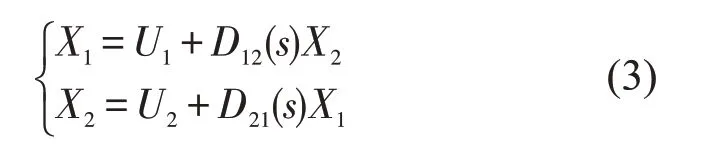
因此

记作

由不变性解耦原理可得:

化简得:

由式(2),(7)可得:

由此可见,引入解耦支路后,系统的传递函数矩阵即转化为对角阵,两个相互耦合的系统解耦为两个相互独立的子系统。
1.2 Smith预估补偿控制器的设计
在非线性PID算法的基础上,参考文献[9-11],设计Smith预估控制器对燃煤锅炉系统中解耦后两个相互独立子系统的滞后环节进行补偿,以减小超调量,优化控制效果。Smith预估补偿的非线性PID控制系统框图如图3。
图3 中,GC(s)为控制器的传递函数,如果控制器的数学模型精确,G0(s)=Gm(s),且不存在负荷扰动(D=0),则Y=Ym,Em=Y-Ym=0,X=Xm(G0(s)表示加入干扰系统的输出,Ym表示未加干扰系统的输出,Em表示两者的差值,X为加干扰没有滞后环节系统输出,Xm表示未加入干扰没有滞后环节系统输出),可用Xm代替X作为第一条反馈回路,实现将纯延迟环节移到控制回路的外边;如果模型不精确或出现负荷扰动,则X≠Xm,Em=Y-Ym≠0,控制精度不能令人满意,Em实现第二条反馈回路。这就是Smith控制策略。
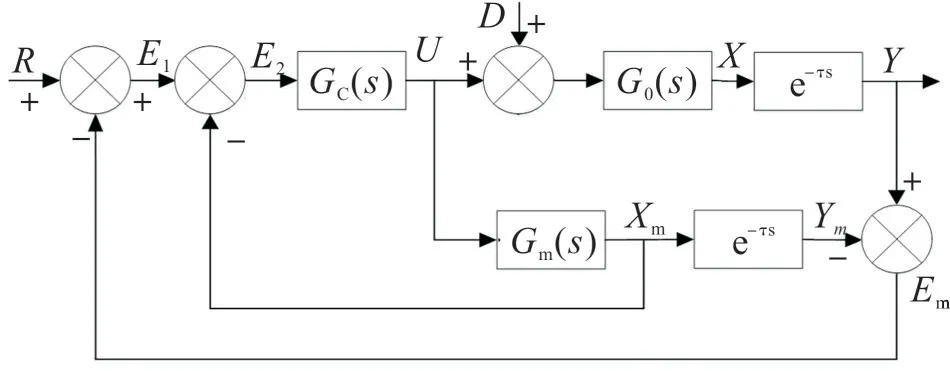
图3 Smith预估补偿的非线性PID控制系统Fig.3 Nonlinear PID control system with Smith pre-estimation and compensation invariance principle
2 Smith预估解耦控制策略的仿真分析
以某发电厂100 MW发电机组410 t/h燃煤发电锅炉为仿真对象,主蒸汽压力设定值为5.8 MPa,排烟氧量体积分数设定值为1.6%。采用前馈补偿综合法和提出的Smith预估解耦控制策略对该燃煤发电控制系统中主蒸汽压力和排烟氧量两个相互耦合的调节回路进行仿真控制。在锅炉机组满负荷的工况下,通过以太网将优化系统与集散控制系统(distributed control system,DCS)工程师站连接,利用OPC(ole for process control)读取主蒸汽压力和排烟氧量的参数,并用力控组态软件进行保存和显示。对锅炉2019 年8 月16 号20点至21点的数据进行采样,采样时间为1 s,共获得3 600组数据,采用Matlab软件的Simulink仿真工具进行参数估计,根据文献[12-13]得到主蒸汽压力和排烟氧量回路的传递函数如下:
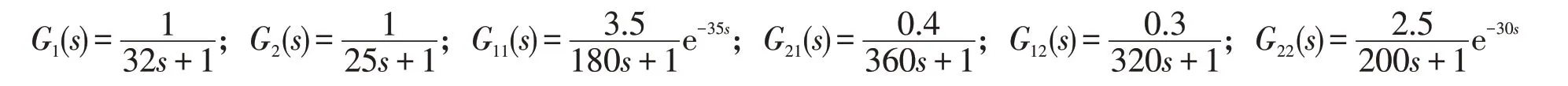
根据不变性解耦原理,由式(9)可得:
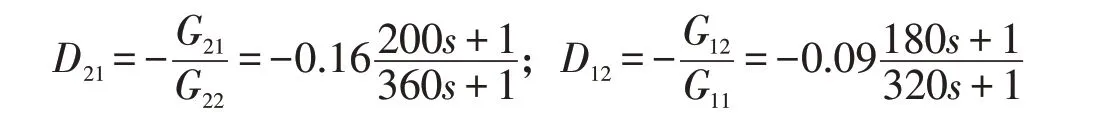
根据Smith预估补偿原理,可知:
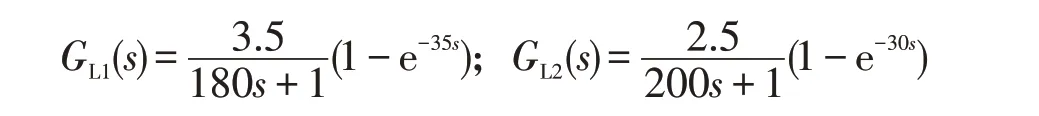
在燃煤锅炉实际运行中,燃煤种类会发生变化,主蒸汽压力也会随之而改变,从而影响送风量,导致排烟氧量改变。相互耦合的两个控制回路,若一个回路出现扰动,则会干扰另外一个回路。根据图1所示锅炉燃烧控制系统解耦控制框图,设定仿真时间为2 000 s,当系统运行1 000 s时,分别在两个控制回路增加幅值为10%的阶跃扰动进行仿真,结果如图4,5。
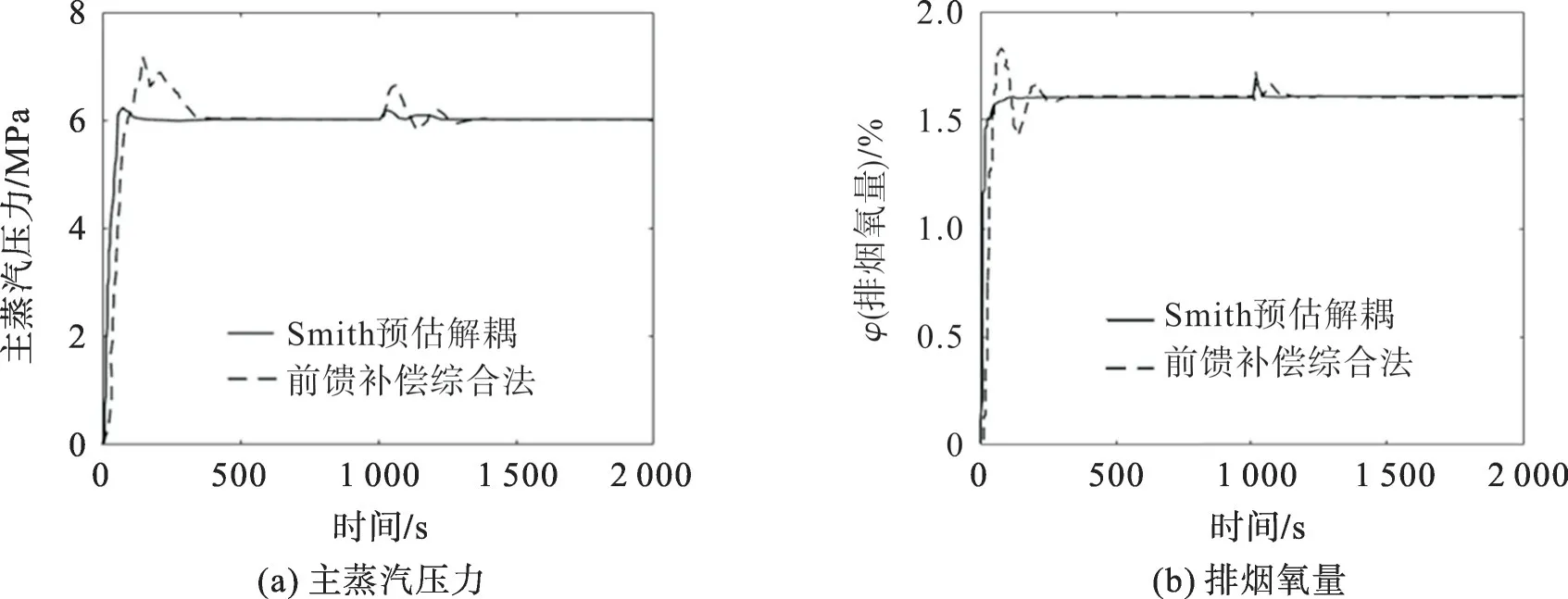
图4 主蒸汽压力控制回路施加扰动时的仿真曲线Fig.4 Simulation curves of the main steam pressure control circuit under disturbance
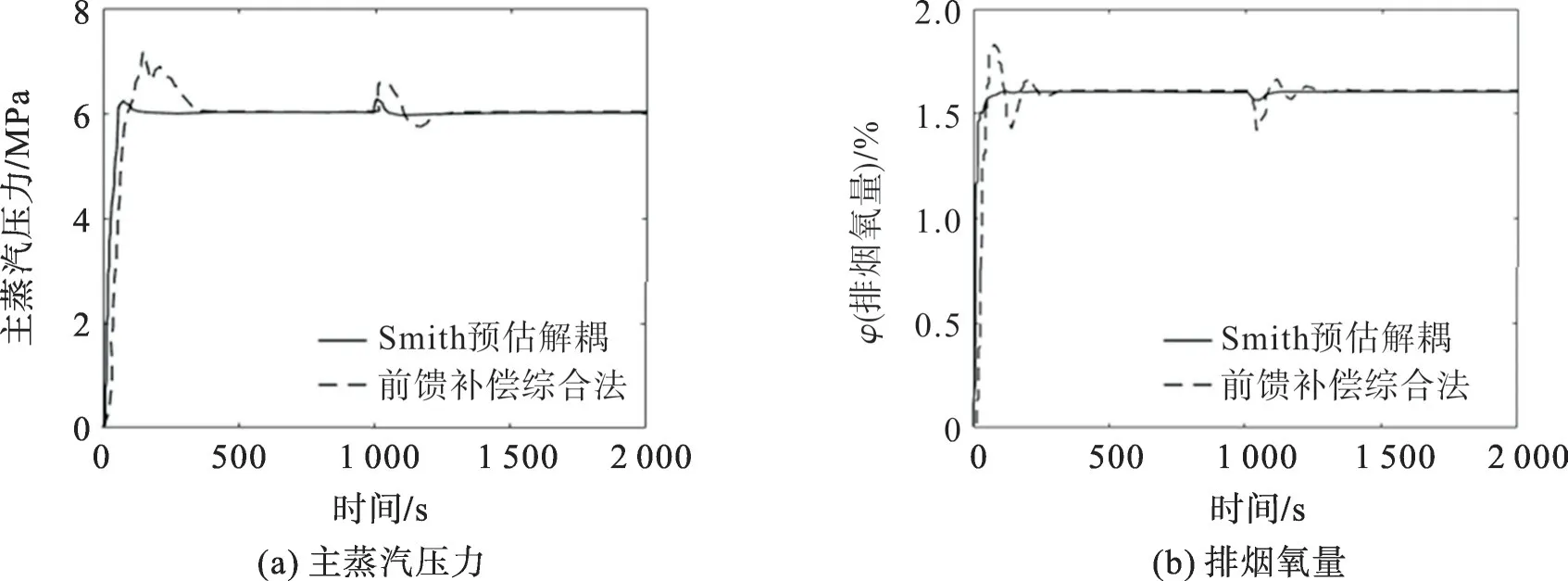
图5 排烟氧量控制回路施加扰动时的仿真曲线Fig.5 Simulation curves of control circuit of oxygen content of exhaust gas under disturbance
从图4 可看出:当主蒸汽压力回路加入10%的阶跃扰动时,本文控制策略下的主蒸汽压力调节时间为83.33 s、超调量为9.50%,前馈补偿综合法下的调节时间为291.66 s、超调量为33.33%;本文控制策略下的排烟氧量调节时间为45.45 s、超调量为6.25%,前馈补偿综合法下的调节时间为136.36 s、超调量为9.75%。从图5可看出:当排烟氧量控制回路加入10%的阶跃扰动时,本文控制策略下的主蒸汽压力调节时间为55.56 s、超调量为8.30%,前馈补偿综合法下的调节时间为222.22 s、超调量为29.10%;本文控制策略下的烟气含有量调节时间为55.56 s、超调量为5.62%,前馈补偿综合法下的调节时间为222.22 s、超调量为13.11%。对比分析表明,提出的解耦控制策略控制效果优于前馈补偿综合法的控制效果。
3 工程应用
火力发电工程中的主蒸汽压力指标设定值为±1.5 MPa,排烟氧量指标设定值为±1.8%。为验证本文提出解耦控制策略的有效性,以某发电厂100 MW发电机组410 t/h锅炉燃烧控制系统为对象进行工程应用。采用AC系列PM590 PLC作为优化控制系统的CPU,PLC通过网线与优化控制系统连接。优化控制系统通过OPC 协议实现与原DCS 系统之间的无扰切换以及数据的采集、处理、输出。同时,使用力控组态软件建立监控组态画面,并对数据的历史趋势进行保存,实现报表统计、考核、参数设置、手自动切换和语言报警等功能。
根据现场工况需求,采用燃料阀门开度、送风机阀门开度和引风机频率值作为操纵变量,主蒸汽压力、炉膛负压和排烟氧量作为被控变量,电机电流、温度等数据作为系统连锁保护条件,控制各被控量在设定值的合理范围内波动,将本文提出的控制策略应用于燃烧系统中,结果如图6,7。图6中数据点时间为2019年11月28日,图7中数据点时间为2019年11月29日。从图6,7可看出:采用本文控制策略时,主蒸汽压力波动范围在设定值±0.3 MPa范围内,排烟氧量波动值在设定值±0.5%范围内;采用前馈补偿综合法控制策略时,主蒸汽压力和排烟氧量波动均比较大。由此可见,本文提出的解耦控制策略再工程应用中也具有良好的控制效果。
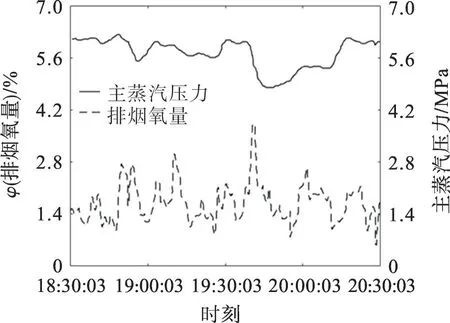
图6 采用前馈补偿法的主蒸汽压力和排烟氧量趋势曲线Fig.6 Trend curves of main steam pressure and oxygen content of exhaust gas with feedforward compensation method
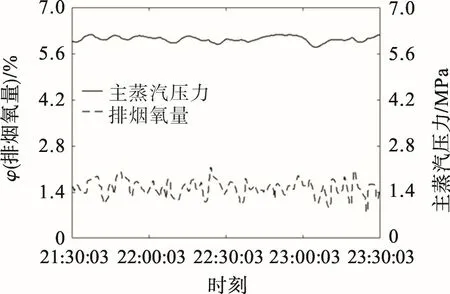
图7 采用解耦控制策略的主蒸汽压力和排烟氧量趋势曲线Fig.7 Trend curves of main steam pressure and exhaust gas oxygen with decoupling control strategy
4 结 论
将Smith 预估补偿器与解耦控制算法相结合,提出一种锅炉燃烧优化的控制策略。Matlab 仿真结果表明,该控制策略能够对主蒸汽压力和排烟氧量的超调量、调节时间等动态性能指标进行有效控制,且控制效果优于前馈补偿综合法。在仿真研究的基础上,将提出的控制策略应用于某电厂100 MW发电机组中,运行结果表明,主蒸汽压力和排烟氧量控制效果均达到控制指标的要求,提出的解耦控制策略具有良好的控制效果。

