角度加权对动态光散射信号噪声影响的抑制作用

王雅静，黄 钰，申 晋，徐亚南，张雯雯，毛 帅

(山东理工大学 电气与电子工程学院，山东 淄博 255000)

1 引 言

与单角度测量相比，多角度动态光散射颗粒测量技术通过对散射样品进行多角度测量，避免了测量未知样品时散射角度选取不当造成的偏差，进而获得更加准确的粒度分布[1-3]。然而，角度数量增多带来的优势也受到诸多因素的制约，包括角度数量[4-5]、角度组合方式[6]以及不同散射角的权重计算[7]等。其中，角度权重的计算是动态光散射由单一散射角扩展至多个散射角获取散射光动态信息的关键环节[1-2]，角度权重的求取会受到角度误差和信号噪声等因素的影响[5]。信号噪声作为影响动态光散射测量准确性的重要因素，在数据反演过程中直接影响粒度分布，这在单角度测量中有较多的分析和研究[8-11]，而在角度加权条件下则未被关注。随着散射角数量的增加，信号噪声也随之增加，噪声在角度加权条件下对测量结果的影响，在很大程度上决定了多角度动态光散角度加权方式在实际测量中的适用性。

角度权重可以通过理论计算得到，即根据Mie 散射理论计算相应散射角的光强，得到对应的权重系数；也可通过实测数据，包括测量对应散射角的静态散射光强或利用各散射角的光强自相关函数(基线)，计算相应的权重系数。一般认为，理论方法求取角度权重系数时，角度权重系数不受自相关数据中信号噪声的影响，而实测法求取角度权重系数时，自相关数据中含有的噪声会通过角度权重的计算影响颗粒粒度反演结果。然而，在近年来的实际应用中，多采用实测方法而非理论方法求取角度权重。这其中既有角度误差影响的原因[12]，也与实测方法逐步改进有关[13]，但从信号噪声的视角，两种加权方法对噪声的抑制作用仍不清晰。本文通过光强均值法[1]和迭代递归法[14]对测量信号噪声影响的抑制作用进行研究，分析和评估噪声环境下角度加权方法对粒度反演的影响，进而为不同测量环境下，特别是为多角度动态光散射在线测量时角度加权法的选择提供依据。

2 不同散射角对粒度信息的贡献差异表征与角度加权机理

r=1,2,…,R，j=1,2,…,Ns，

(1)

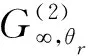
i=1,2,…,N，j=1,2,…,Ns，

(2)

式中：衰减线宽Γ=DTq2，颗粒平移扩散系数DT=KBT/3πηD，散射矢量q=4πn[sin2(θr/2)]/λ，n，λ分别为悬浮介质的折射率、真空中光的波长；hθr(Di)为颗粒粒度光强分布，表示散射角θr处粒度在[Di,Di+1]的所有颗粒的散射光强分数。归一化的散射光强分数为：

(3)

散射光强分数为:

hθr(Di)=kθrCI,θr(Di)f(Di),

(4)

其中：kθr为角度权重系数；CI,θr(Dr)为Mie散射

光强分数，表示粒度为Di的颗粒在角θr处的散射光强分数；f(Di)代表粒度为Di的颗粒在角θr对散射光的贡献。

将式(4)带入式(2)得到:

(5)

式(5)的矩阵形式为:

(6)

则多角度电场自相关函数的矩阵形式为:

(7)

式中：g=[gθ1;gθ2;...;gθm]，为多角度电场自相关数据；A=[kθ1Aθ1;kθ2Aθ2; ...;kθmAθm]，为相应的核矩阵；f为待求粒度分布。

在散射光场中，散射强度分布与散射颗粒粒度分布满足:

X(θr,Di)=C(θr,Di)f(Di),

(8)

式中Mie散射光强分数CI,θr(Di)作为换算因子，可由Mie理论计算得到，其分布如图1(a)所示。

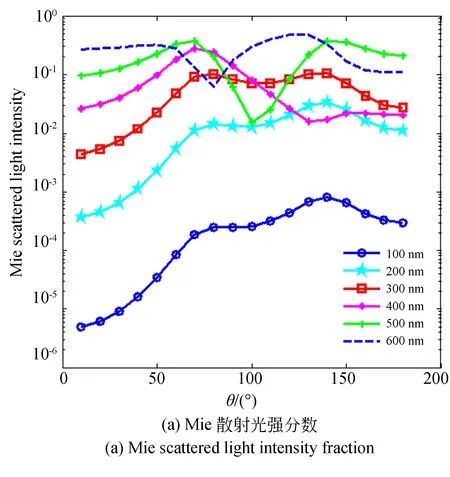
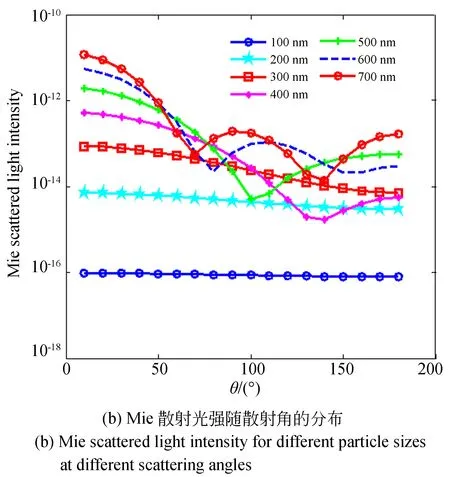
图1 散射角对不同粒度颗粒的影响

散射光强分布不仅受颗粒大小影响，还与散射角度有关。在散射颗粒大于350 nm时，Mie散射光强随散射角呈振荡变化(图1(b))，同一颗粒体系的散射光在不同散射角存在很大差异，这正是多角度测量大于350 nm颗粒时，能够兼顾不同角度散射光强的贡献，得到更为准确的测量结果的原因。多角度测量，需要确定散射角θr处对粒度分布信息贡献的差异，这一差异是通过角度权重系数进行表征的。由式(3)和式(4)得到理想角度权重系数:

(9)

其中f(Di)是未知的，因此不能用于求取角度权重系数。但从式(9)可以看出，权重系数kθr与颗粒在散射角度θr处散射光强均值的倒数〈Iθt〉-1具有比例关系，定义无量纲的角度权重系数比为散射角θr处角度权重系数与散射角θ1处的角度权重系数的比，根据两者关系即可获得角度权重系数。式(7)可写成:

(10)

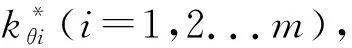
2 不同噪声水平下两种加权方法对反演结果的影响分析

为定量分析信号噪声通过加权对测量结果的影响，采用半对数函数及其组合模拟3组单峰S1(200 nm)，S2(450 nm)，S3(600 nm)和1组双峰颗粒S4(500/800 nm)的数据，计算在6个角度(30°，50°，70°，90°，110°和130°)的光强自相关数据，同时采用光强均值法及迭代递归法进行角度加权，利用截断奇异值方法对自相关函数进行反演。半对数函数表达式为:

(11)

式中：f(Di)是颗粒粒度分布，a为分布系数，D1为峰值处颗粒粒度，σ1为标准偏差。通过调整半对数函数参数可以获得相应的粒度分布。4组颗粒体系的参数如表1所示。模拟实验条件为：KB=1.380 7×10-23J/K，分散介质折射率n=1.33，入射光在真空中的波长λ=632.8 nm，绝对温度为T=298.15 K，介质黏度系数η=0.89×10-9g/(nm·s)。

信号噪声添加形式为：

(12)

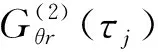
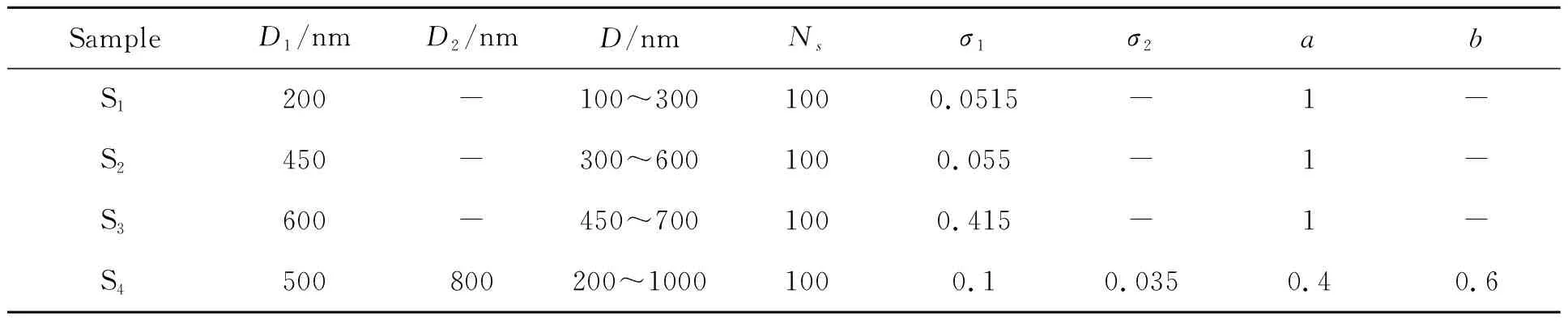
表1 4组颗粒的模拟参数

为定量评价颗粒粒度的反演效果，引入峰值粒度误差E、峰值P，峰值比R和分布误差V4个性能指标。对于单峰与双峰分布颗粒系分别采用E，P，V与E，R，V描述反演结果与真实分布的接近程度。峰值粒度误差越小；峰值与模拟峰值越接近；模拟分布的峰值比与反演分布的峰值比越接近；分布误差越小，表示反演的颗粒粒度分布与实际粒度分布越接近。

R=P1:P2:…Pn

(13)

式中：Dsim和Dinv分别表示模拟分布和反演分布中峰值粒度，P表示峰值，fsim和finv分别表示模拟分布和反演分布。

图2～图5分别为4组颗粒体系的反演结果。表2～表5为4组颗粒体系反演的性能参数。其中，“Sim PSD”代表模拟粒度分布，“Wa”代表光强均值角度加权方法，“Wir”为迭代递归角度加权方法。

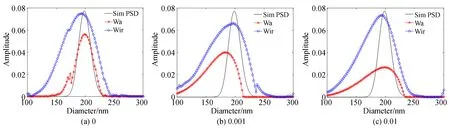
图2 200 nm单峰颗粒在不同噪声下光强均值和迭代递归法的反演结果Fig.2 PSDs of 200 nm unimodal particle using Wa and Wir methods at different noise levels

从图2和表2可以看出，对于200 nm单峰小颗粒体系，无信号噪声时，采用两种方法进行角度加权，反演得到的峰值误差结果无显著差异，但迭代递归方法加权对小颗粒粒度分布略有展宽，表现出较大的分布误差。随着噪声的增加，迭代递归法方法加权所得反演结果的性能指标无显著变化，而光强均值法进行角度加权所得结果的峰值误差明显增大，分布误差也随之增大。

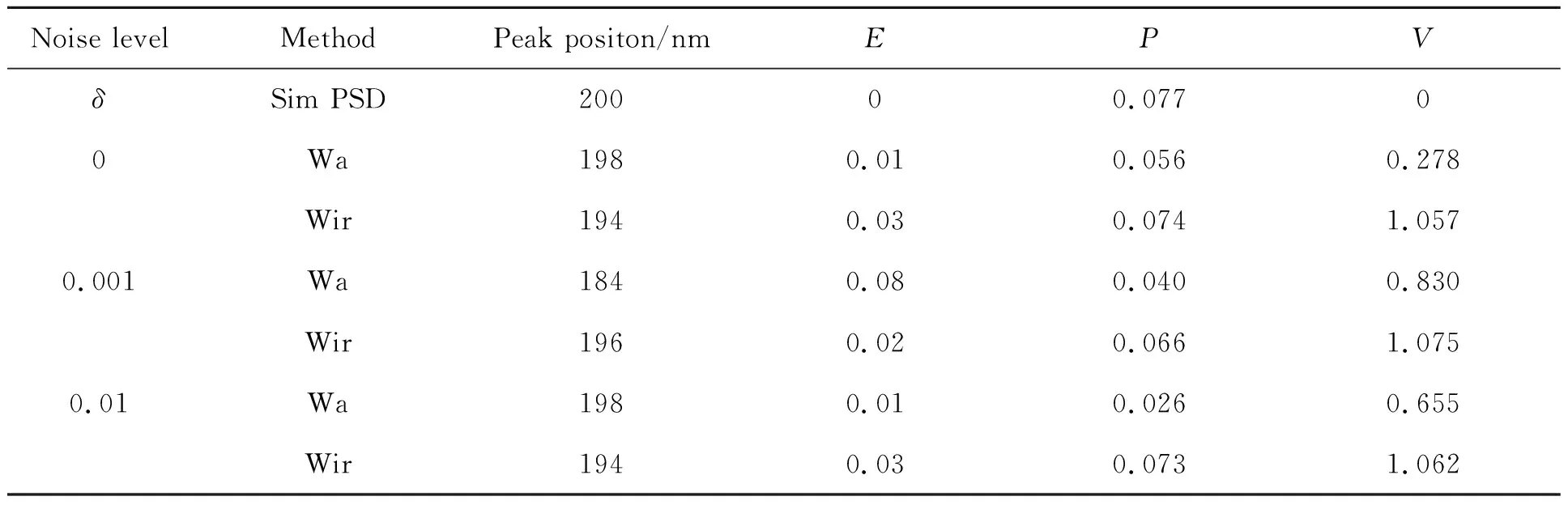
表2 200 nm颗粒在不同噪声水平下光强均值法和迭代递归法的性能参数

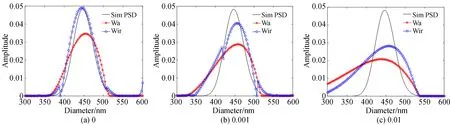
图3 450 nm单峰颗粒在不同噪声下光强均值和迭代递归法的反演结果Fig.3 PSDs of 450 nm unimodal particle using Wa and Wir methods at different noise levels

对于450 nm单峰中等粒径颗粒(图3和表3)，在无信号噪声时，采用两种方法进行角度加权，反演得到的性能参数无显著差异，光强均值法进行角度加权，所得峰值误差略有增大。随着噪声的增加，光强均值法所得峰值误差呈愈加明显的趋势，分布误差也随之增大。迭代递归方法加权所得的峰值误差和分布误差随噪声增加也有增大的趋势，但增幅明显小于光强均值法。

表3 450 nm颗粒在不同噪声水平下光强均值法和迭代递归法的性能参数

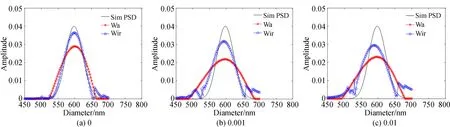
图4 600 nm单峰颗粒在不同噪声下光强均值和迭代递归法的反演结果Fig.4 PSDs of 600 nm unimodal particles using Wa and Wir methods at different noise levels

表4 600nm颗粒在不同噪声水平下光强均值法和迭代递归法的性能参数

Tab.4 Performance parameters of 600 nm unimodal particles using Wa and Wir methods at different noise levels

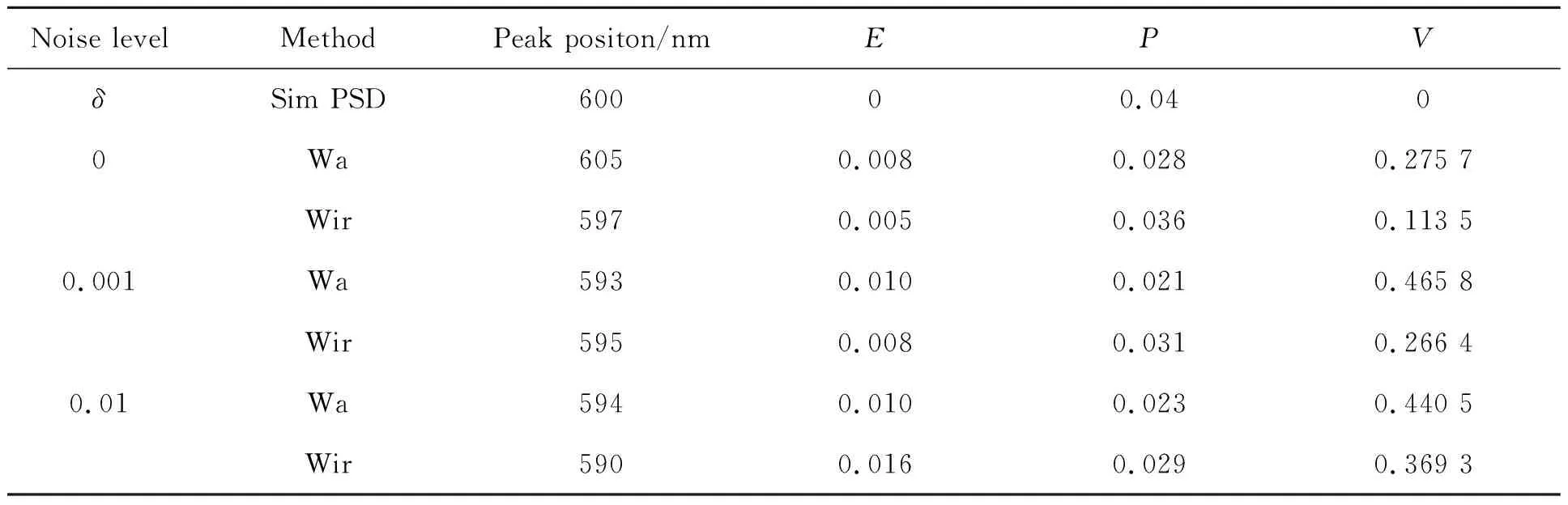
Noise levelMethodPeak positon/nmEPVδSim PSD60000.0400Wa6050.0080.0280.275 7Wir5970.0050.0360.113 50.001Wa5930.0100.0210.465 8Wir5950.0080.0310.266 40.01Wa5940.0100.0230.440 5Wir5900.0160.0290.369 3

对于600 nm单峰大颗粒(图4和表4)，表现出与450 nm单峰中等粒径颗粒相同的结果，即在无信号噪声时，采用两种角度加权方法反演得到的性能参数无显著差异，光强均值法加权所得峰值误差略大。随着噪声的增加，光强均值法所得峰值误差和分布误差的增大更为显著。

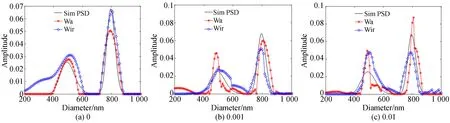
图5 500/800 nm双峰颗粒在不同噪声下光强均值和迭代递归法的反演结果Fig.5 PSDs of 500/800 nm bimodal particles using Wa and Wir at different noise levels

表5 500/800nm颗粒在不同噪声水平下光强均值法和迭代递归法的性能参数

Tab.5 Performance parameters of 500/800 nm bimodal particles using Wa and Wir methods at different noise levels

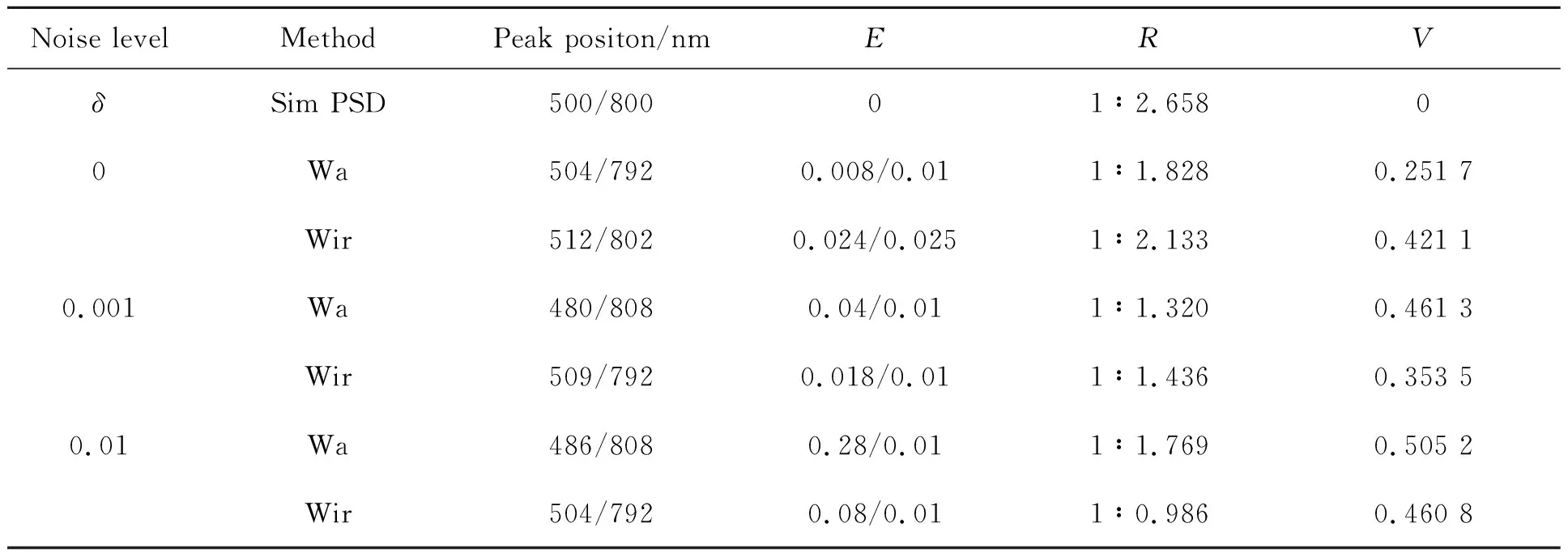
Noise levelMethodPeak positon/nmERVδSim PSD500/80001∶2.65800Wa504/7920.008/0.011∶1.8280.251 7Wir512/8020.024/0.0251∶2.1330.421 10.001Wa480/8080.04/0.011∶1.3200.461 3Wir509/7920.018/0.011∶1.4360.353 50.01Wa486/8080.28/0.011∶1.7690.505 2Wir504/7920.08/0.011∶0.9860.460 8

对于500/800 nm双峰分布(图5和表5)，在无信号噪声时，两种角度加权方法得到的性能参数无显著差异，但迭代递归方法加权表现出较大的分布误差。但随着噪声增加，光强均值法进行角度加权所得结果的分布误差越来越大，迭代递归法方法加权所得结果则趋于减小。

上述结果可以看出，在无噪声情况下，两种角度加权方法得到的反演结果没有显著差异，作为理论方法的光强均值法加权，由于是根据Mie 散射理论直接计算所有散射角的权重，避免了权重随机误差导致的偏差。而迭代递归方法角度加权系通过第一个参考角度逐个计算各角度的权重，其权重计算依赖第一个参考角选择和后续角度的修正。对于小颗粒，由于不同角度的散射光强没有显著变化(图2)，导致后续角度没有修正作用，这一情况随着颗粒的增大有所改善。

随着信号噪声的增加，两种角度加权方法得到的反演结果都呈现变差的趋势，主要表现在峰值和分布误差变大。但是，迭代递归方法角度加权的反演误差显著低于光强均值法。产生这一现象的原因在于其权重计算方式：迭代递归方法是从参考角开始逐次增加角度反演粒度分布，每次反演结果和上一次结果进行比较后计算各角度的权重，每次的权重计算都是对上一次计算结果的调整和更新，通过角度权重的调整抵消噪声导致的粒度分布误差，从而显现出“去噪”性能。

3 实验数据的反演分析

为了验证模拟结论，对306/974 nm的标准聚苯乙烯乳胶颗粒组成的双峰颗粒体系进行了测量。测量实验条件为：He-Ne激光器，测量温度298.15 K，分散介质为1 mmol/L NaCl配制的悬浊液，散射角分别为30°，50°，70°，90°，110°和130°。对获得的动态光散射数据分别采用光强均值法和迭代递归法进行角度加权处理数据，并采用截断奇异值反演算法进行反演获得粒度分布，用L曲线法获得正则参数，反演结果和性能参数分别如图6和表6所示。

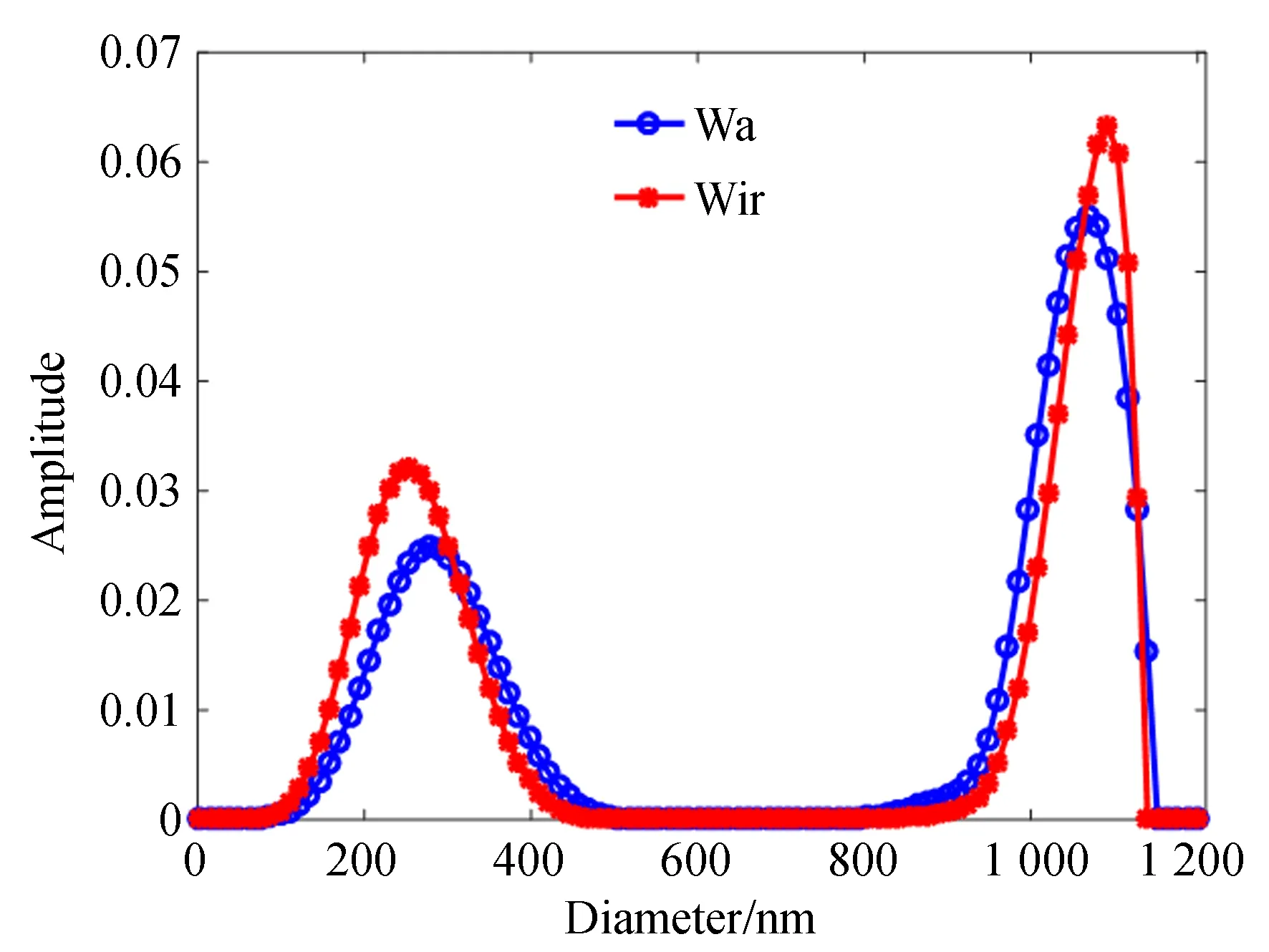
图6 306/974 nm双峰颗粒在光强均值法和迭代递归法的反演结果Fig.6 PSDs of 306/974 nm bimodal particles using Wa and Wir methods

表6 306/974nm双峰颗粒在不同角度加权方法下的性能参数

Tab.6 Performance parameters of 306/974 nm bimodal particles at different angular weighting methods

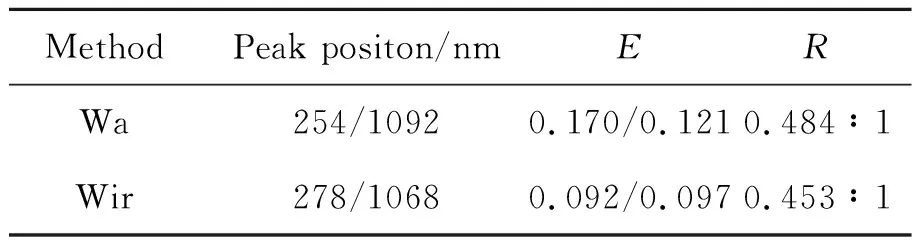
MethodPeak positon/nmERWa254/10920.170/0.1210.484∶1Wir278/10680.092/0.0970.453∶1

从图6和表6可以看出，对于306/974 nm双峰颗粒体系，与采用光强均值法处理数据相比，采用迭代递归方法处理数据进行角度加权时，小颗粒峰值粒度误差由0.170降到了0.092，大颗粒峰值粒度误差由0.121降到了0.097，峰值高度比分别为0.484∶1和0.453∶1。

4 结 论

在多角度动态光散射颗粒测量中，信号噪声对测量结果有着极大的影响，角度加权是左右噪声对测量结果影响的一个重要因素。不同的角度加权方法对测量信号噪声影响的抑制作用不同，通过光强均值及迭代递归角度加权方法研究测量信号噪声影响的抑制作用。对于单峰小颗粒粒度分布，无信号噪声时，采用光强均值法和迭代递归方法进行角度加权，反演得到的峰值误差结果无显著差异，但迭代递归方法加权对小颗粒粒度分布略有展宽。随着噪声的增加，迭代递归法加权所得反演结果的性能指标无显著变化，而光强均值法进行角度加权所得结果的峰值误差明显增大，分布误差也随之增大。对于中、大颗粒，在无信号噪声时，采用两种方法进行角度加权，反演得到的性能参数无显著差异，光强均值法进行角度加权，所得的峰值误差略有增大。随着噪声的增加，光强均值法所得峰值误差增加呈愈加明显的趋势，分布误差也随之增大。迭代递归方法加权所得的峰值误差和分布误差也随噪声增加趋于增大，但增幅明显小于光强均值法。对于双峰分布，迭代递归法角度加权反演的分布误差随着噪声增加也呈现出小于光强均值法角度加权所得误差的趋势。该结果与常规认知不相吻合，其原因在于迭代递归法通过在各个散射角逐次反演和比较粒度分布，通过角度权重的“修正”抵消了噪声导致的粒度分布误差，从而显现出抵御噪声影响的“去噪”性能，而采用光强均值法计算角度权重，尽管权重计算采用无噪声的理论数据，但它对由于角度增加引起的信号噪声增加却无抑制作用。因此，在噪声较大的测量环境下，如现场测量等，宜采用迭代递归方法进行多角度测量的角度加权。