超声电机速度与位置的高精度控制

陈 宁，郑杰基，范世珣，李华峰，范大鹏*

(1. 国防科技大学 智能科学学院，湖南 长沙 410073;2.南京航空航天大学 航空学院，江苏 南京 210016)

1 引 言

近年来，随着超声电机在空间机器人、生物医学微操作设备等领域的应用，其速度与位置控制精度的要求也越来越高[1-2]。而超声电机将压电陶瓷的微观高频振动转化为输出转子的宏观旋转运动的过程中，非线性、多变量、强耦合的特性引起了系统模型的不确定性[3]，使电机呈现出复杂的动力学行为，难以获得精确的模型。同时，由于μs级调控、μm级振动的特点，能否充分利用微观特性使电机更精细地判断与调整运动状态，成为最终速度位置控制性能优劣的根本性问题。

在速度控制层面，重点是如何实现电机的速度平稳性控制，人们主要采用速度闭环控制[4-5]和频率跟踪控制[6]两种方式。传统的速度闭环控制既从结构上缺乏位置环的辅助作用，也忽略了超声电机μs级快速定位的优势。而在频率跟踪控制上则涌现出以孤极电压[7]、阻抗角[8-10]为反馈量的多种控制方式，但由于频率跟踪截取的多为定转子摩擦传力前的陶瓷机电信号，难以实现较好的控制效果。近年来，随着控制理论的发展，学者提出了诸如模糊控制[11]、神经网络控制[12]、混沌控制[13]等超声电机速度控制策略。虽然取得了一定成果，但是多数因模型集获取困难及训练复杂等原因难以在工程上广泛应用[14-15]。从位置控制来看，主要难点在于高分辨率定位，这需要精确的开环或闭环步进运动，特别是开环步进模式下的高分辨率运动，对于紧凑空间的精密定位应用是很有意义的。若想把握开环步进运动的规律，需要尽可能地细化其中的启动关断过程，尤其是当周期数较小时(N≤10)，关断过程的动态特性对步进位移量的影响不能忽略[16]。因此，为了实现高分辨率的步进运动，有必要分析少周期数条件下关断过程的规律，并提出行之有效的位置增量预测方法。

综合上述分析，速度平稳性控制与位置分辨率控制构成了超声电机控制性能提升的两个核心问题。二者均要建立在对电机参数调控机理以及微观状态演变的建模分析上。因此，本文从连续运动与步进运动两种模型机理进行研究，目的在于充分利用电机的自身特性，运用工程上快速易行的方法实现控制目标。在速度平稳性控制上，提出并辨识了多输入多输出速度模型，设计了双环复合的速度控制策略；在位置分辨率控制上，开展了电机步进运动特性尤其是关断过程速度规律的研究，提出步进量预测模型，并通过优化驱动参数实现电机的高分辨率步进运动。

2 连续运动与步进运动机理分析

超声电机在两相正弦波的共同激励下工作，通过驱动参数和波形关断时间的控制可以实现连续运动与步进运动，分别对两种模型及其影响因素进行分析。

2.1 连续运动机理

2.1.1 多参数调速模型

超声电机的运动及控制的实质在于改变行波的振幅、速度以及质点的椭圆轨迹，其相应的控制量有两相驱动电压幅值(u)、频率(f)和相位差(α)。由行波的运动方程可知，波峰处的切向速度可以表示为：

(1)

式中:ξ为定子振幅，h为定子厚度的一半，ω=2πf为驱动的角频率，n为行波振动的波节数。可以看出，一定频率和相位差的峰值速度与定子振幅ξ呈线性关系，而定子振幅ξ与电压幅值u成正比，因此速度值νs与激励幅值u满足线性关系。同时根据文献[14-15]，在一定幅值和相位差条件下定子速度峰值与频率呈指数关系。考虑到相位差不为±90°时，定子的两相驻波波形不正交，在带来波形畸变的同时也将使速度变化规律更加复杂，因此在控制时只考虑相位差α为±90°时的速度模型，从而将转子速度的稳态值等效为定子的切向速度峰值。进一步整合超声电机转子转速的动态传递函数H(s)，得到的转子速度表达式为：

vr=(au+b)e(cf+d)H(s),

(2)

式中a,b,c,d为待定系数，将通过后面的辨识获得。

2.1.2 速度平稳性及表征

超声电机的速度时刻处在变化当中，主要成因是电机轴线在加工和装配过程中存在角度偏差，使得摩擦界面接触不平衡，周向压力分布不均[17]。定性来看，超声电机在工作状态下，接触压力大的一侧接触范围较大，阻止区较大，定子振幅较小，导致速度偏小；而接触压力小的一侧接触范围窄，驱动区相对较大，定子振幅较大，速度较高[18]。由于速度分布在周向的不一致，超声电机转动一圈，速度将会产生持续的周期性波动，从而加重定转子相对速度差异带来的滑移，在增加摩擦损耗降低效率的同时还会影响电机服役寿命。为了减少这类误差，不仅需要改进定转子结构、提高制造精度，还需要研究波动误差抑制或补偿方法。

(3)

式中νr为电机实时测得的速度。显然速度平稳性控制的最终目标就是尽可能降低控制残差的占比。

2.2 步进运动机理

步进运动是指超声电机在间歇性的电压激励下产生的反复启停运动过程，其速度规律不再是连续运动状态下速度均化的结果，而是包含了启动、运行、关断等响应全过程。假设当驱动信号周期数发生变化时，启动后的转速曲线是沿着同一轨迹逐渐延伸的。如图1所示，将启停过程转速曲线以关断点Ai为界分为启动与关断两个阶段，并定义Bi为关断后电机运动的自锁点。

图1 不同周期数的速度曲线Fig.1 Speed curves under different period numbers

显然，在不同的周期数条件下，启动阶段与关断阶段的速度函数可以分别表示为：

(4)

(5)

式中：ξs与ξp代表启动阶段与关断阶段的阻尼系数，ωs与ωpi则表征各自传递函数的谐振频率，Ks与Kp为各自的增益系数。

此时可以采用面积包络法计算位移增量，通过计算速度曲线与坐标轴的面积得到步进量Si，如式(6)所示：

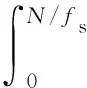
(6)

式中:N为激励波形的周期数，fs为激励电压的频率，tp为最终的关断时间。

3 高精度测试装置

为了辨识超声电机的速度模型，也为了能在控制中实现更高的速度位置分辨精度，本文在多参数综合测控系统中的编码器进行替换。所选用的编码器为美国MicroE Systems公司的分立式增量编码器，主要由光栅盘、读数头及细分电路构成，如图2所示。其中，光栅刻线数为16384(214)，即物理细分为14位，而细分电路模块对读数头输出的脉冲信号进行1 024(210)的细分处理，即电气细分为10位。两者综合后编码器的整体分辨位数为24位，检测分辨率为0.375 μrad，能够满足超声电机高精度控制的反馈与评估需求。所采用的电机为新研的PMR60-PI1电机，集成了新型压电陶瓷与摩擦功能材料，具有较好的工作稳定性。

图2 高精度编码器组成Fig.2 Composition of high-precision encoder

4 模型辨识及控制实验

为了实现电机的高精度速度与位置控制，对模型中的待定参数进行辨识和分析，进而提出有针对性的高平稳性速度控制策略与高分辨率位置控制策略。

4.1 高平稳性速度控制

4.1.1 连续运动多参数模型辨识

在多参数模型辨识环节，设定电压幅值为[200 V,260 V]，频率测试区间为[42 kHz ,44 kHz]，在相应的幅值与频率作用下，求取电机运行10 s后的平均速度，得到的稳态速度点如图3所示。

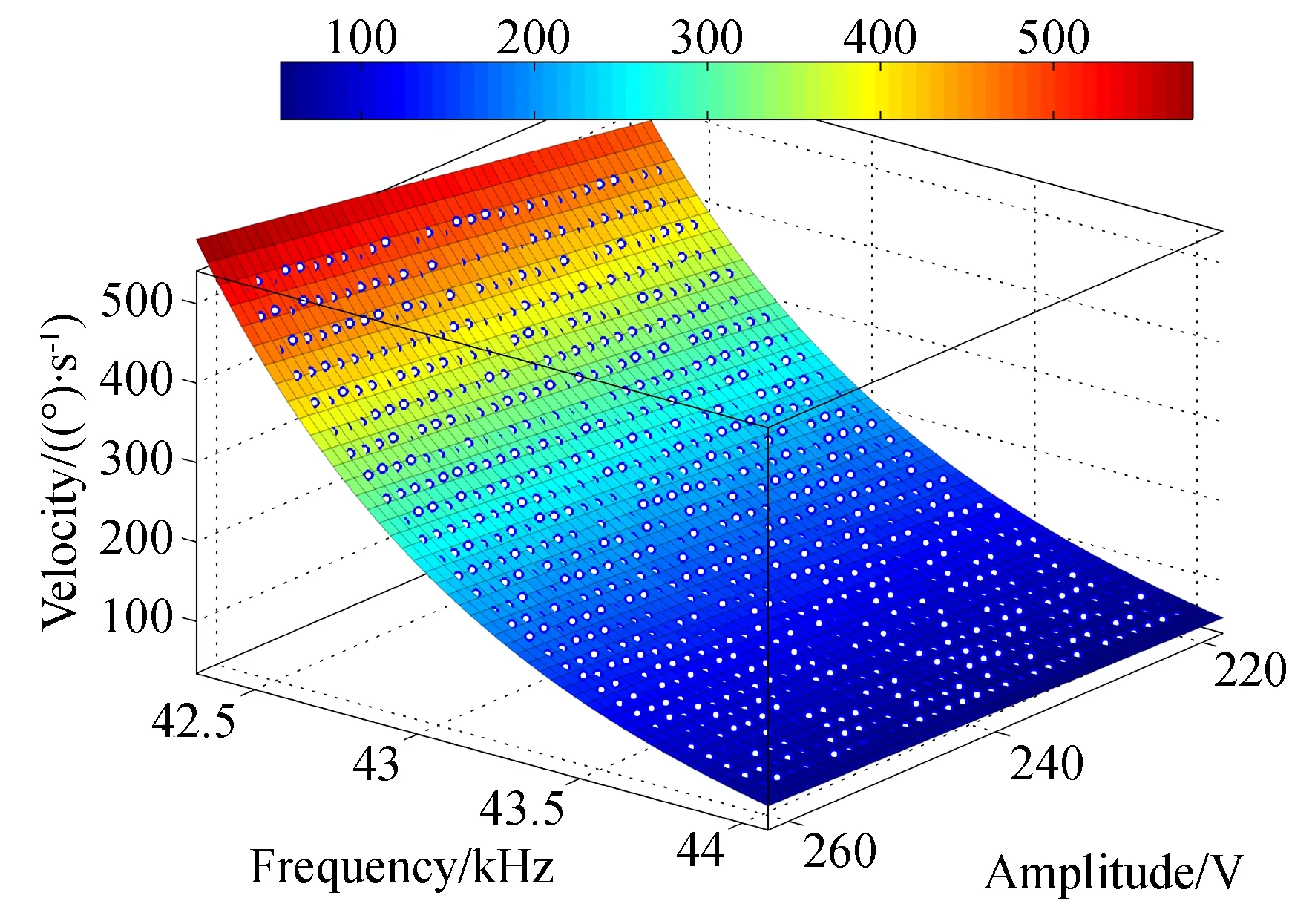
图3 幅值-频率-速度关系的三维曲面Fig.3 Three-dimensional speed curves under different amplitudes and frequencies

按照线性关系与指数关系相乘的表达式，利用Levenbert-Maquetety规则下的非线性最小二乘算法对数据进行拟合，得到的综合模型为：

νr(u,f)=(9.39u+10.29 )e(58.16 -1.411f).

(7)

在辨识分析系统动态部分时，以幅值为输入，速度为输出，扫频区间为0.1～200 Hz，得到如图4所示的幅频与相频曲线。可以看出，不同驱动参数归一化后的扫频曲线吻合度比较好，可以统一用一种传递函数进行表征。

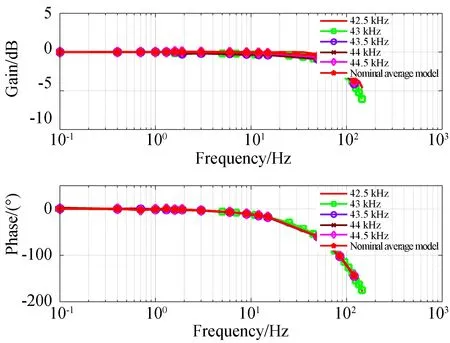
图4 不同驱动参数的幅值扫频曲线Fig.4 Amplitude sweeping curves under different driving parameters

运用最小二乘算法对图4中归一化后的扫频模型进行辨识，参数速度模型的动态部分可以表示为:

H(s)=

(8)

结合上述稳态部分与动态部分，在Simulink上建立起如图5所示的超声电机多参数调速模型。

图5 多参数调速模型Fig.5 Multi-parameter speed model

4.1.2 双环复合速度控制策略

4.1.2.1 仿真分析

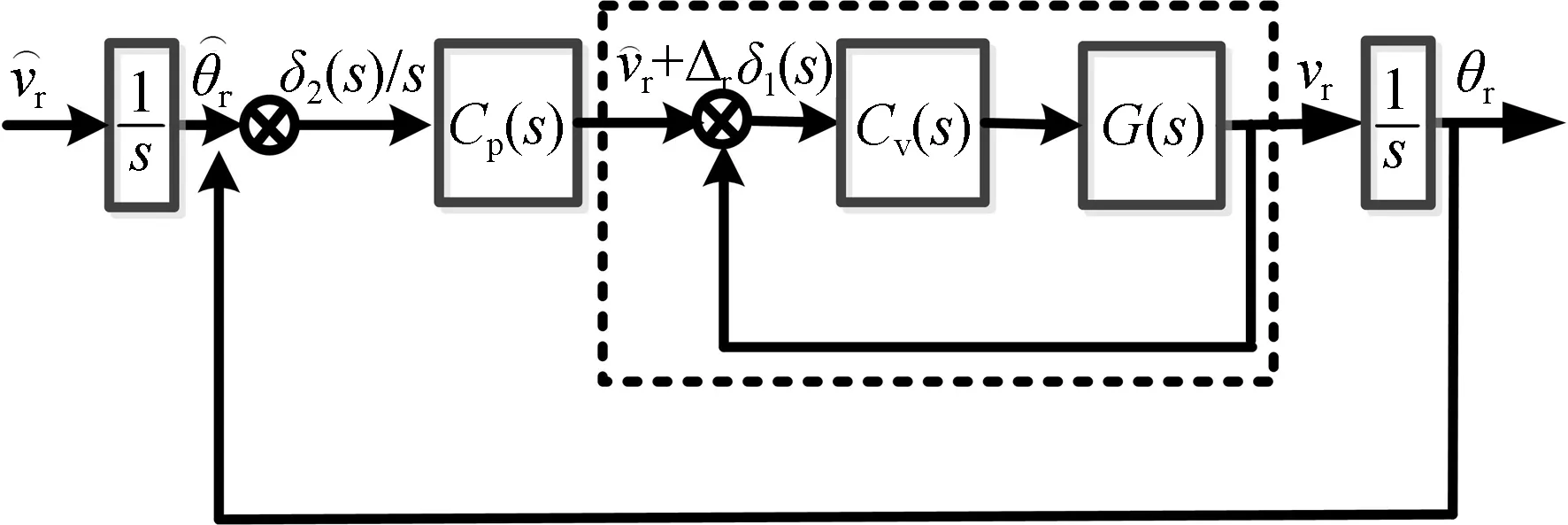
图6 速度平稳性控制框图Fig.6 Control diagram of speed stability

从控制框图上看，单一速度环控制时速度误差的表达式为：

(9)

而采用“位置环+速度环”双环控制所获得的速度误差表达式为:

(10)

因而两个误差的比值为:

(11)

如果在实施时，通过调节能控制:

(12)

当速度指令为72 (°)/s时，设计速度环PI控制器的参数Kp=2，Ki=150，位置环PI控制器的参数为Kp=70，Ki=1。通过仿真获得式(11)误差传递函数的波特图，如图7所示。结果证实了当电机的速度波动处于10 Hz的频带内，所提出的双环控制器都能有效补偿波动影响，在仿真条件下能够获得优于单环控制的效果。

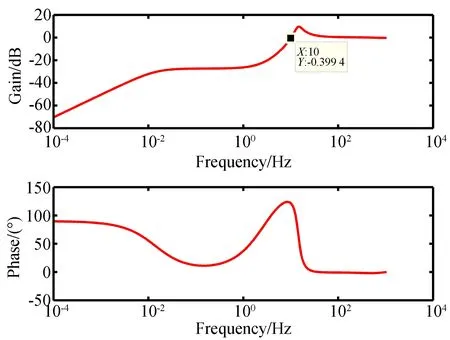
图7 误差比值扫频曲线Fig.7 Sweeping curves with error ratio of different period numbers

从图7可以看出，双环控制能够获得比单环控制更小的稳态误差。这是由于双环控制既能够得到更高的幅值及相位裕度，也可以充分发挥超声电机快速定位的优势，使得速度环控制后的残差在位置环内进一步得到消除，从而提升整体的速度控制精度。

4.1.2.2 实验结果

与仿真相似，当速度指令为72 (°)/s时，通过调节，设计速度环PI控制器的参数Kp=2，Ki=150，位置环PI控制器的参数Kp=70，Ki=1。通过实验，将单速度环控制与双环复合控制的速度控制效果进行比较(图8)，可以发现双环复合控制的控制误差(0.44%)约为单速度环控制误差(0.89%)的一半，说明双环复合的方法能够进一步补偿速度环的残差。

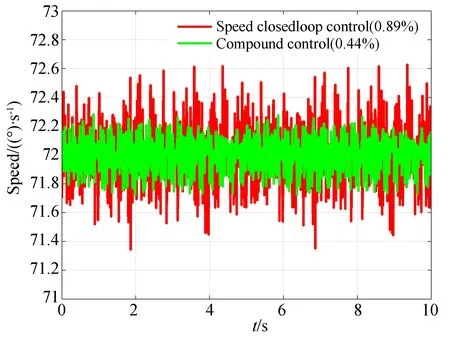
图8 速度平稳性控制对比Fig.8 Block diagram of performance evaluation

将双环复合的控制策略应用到40,50,60,70 (°)/s的恒速控制中，结果如图9所示。由图可知，每组控制后上升时间约为22 ms，速度稳定度均低于0.44%。

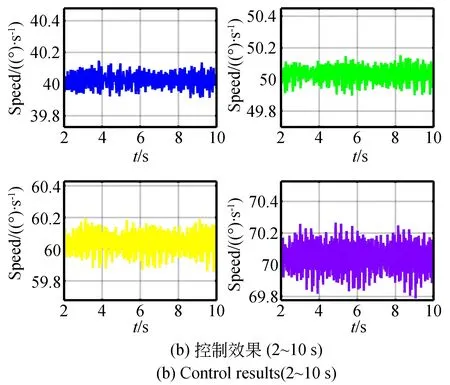
图9 速度平稳性控制效果Fig.9 Control results of speed stability

4.2 步进运动位置控制

通过驱动电源对超声电机实施控制，即由驱动电源的通、断，使电机产生间歇性的起、停动作而实现步进运动[18]。为了获得不同参数条件下的步进运动规律，测试了不同周期数的转速响应曲线，进而提出步进量的预测与控制模型。

4.2.1 步进量模型辨识

为了得到步进量预测的稳定区间，测试了不同周期数的转速曲线，如图10所示。可以看出，周期数较少的启动曲线与周期数较多的启动曲线部分重叠，表明了相同激励参数条件下的电机启动过程呈现较好的可重复性，而从关断后过零部分的速度响应看，不同周期数的关断曲线也表现出了相似的振荡特征。

图10 不同周期数的启停速度响应曲线Fig.10 Startup-stopping speed response under different period numbers

结合图1与式(4)，对速度响应曲线进行分段二阶函数的辨识。首先是启动段，通过辨识可以得到的启动阶段的传递函数Gs为：

(13)

其次是关断段速度传递函数的辨识，图11为辨识得到的关断段的增益、阻尼系数、固有频率以及每一个周期数下的关断点速度。

辨识结果表明，周期数小于10时模型参数的变化趋势相对稳定，这是由于周期数在[1,10]之内时，速度仍处于上升的初始阶段，未到达阶跃响应的上升节点，即稳态速度的0.707，没有突破弹性波动的极限，因此断电后的回复过程相对比较接近，综合曲线后确定关断过程阻尼系数在0.012，自然频率为4 200 rad/s。对辨识后的参数与关断点速度之间的关系进一步进行探索，如图12所示，模型增益与关断点转速成正比，且比例系数为0.197。根据上述分析，建立了如式(14)所示的关断速度的传递函数，该表达式将关断过程的传递函数与关断点的速度相互关联，从而实现了启动段与关断段的衔接。

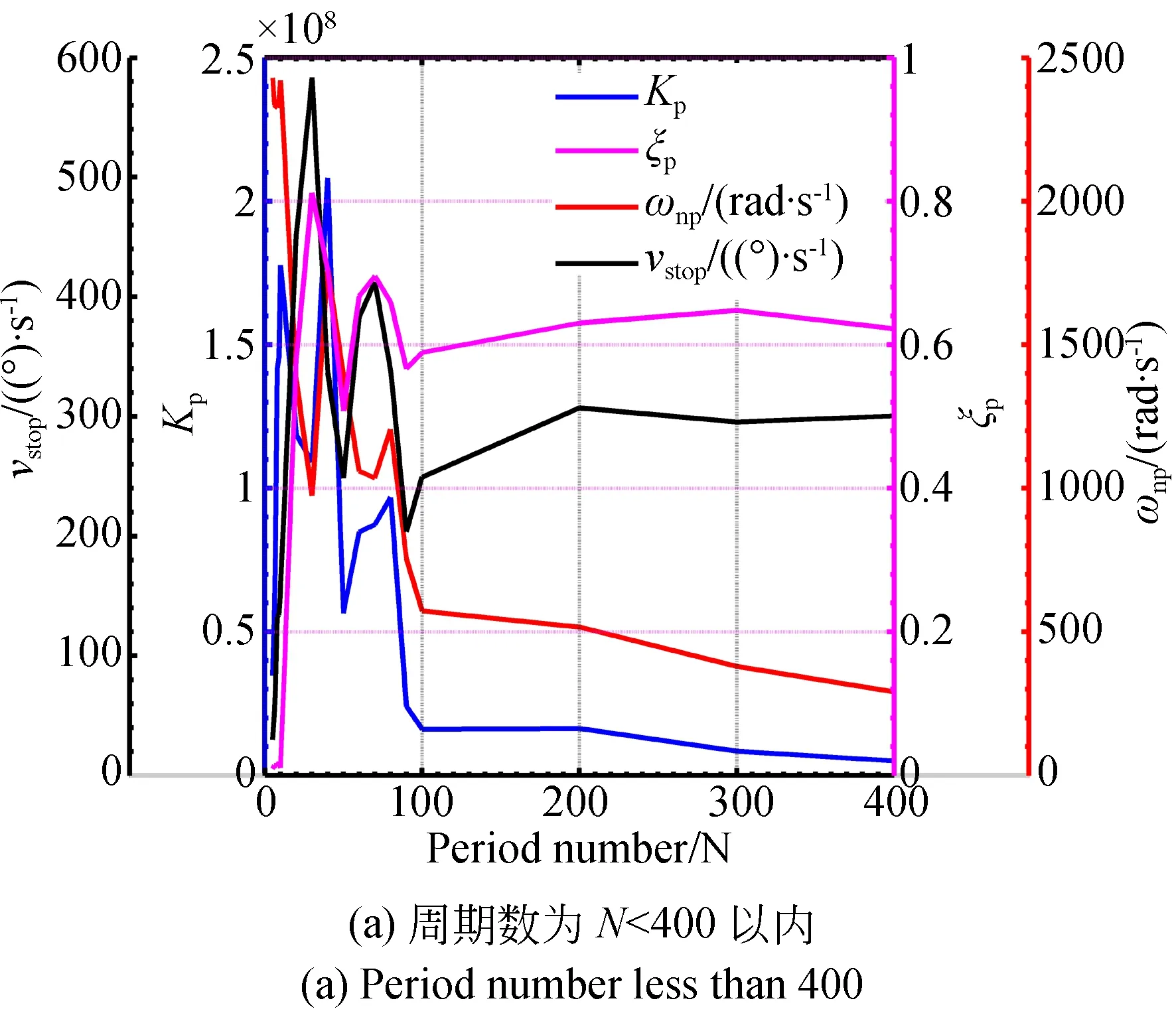
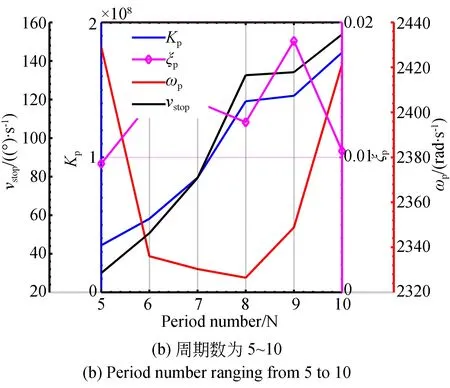
图11 辨识得到的关断阶段的模型参数Fig.11 Identified parameters of stopping process

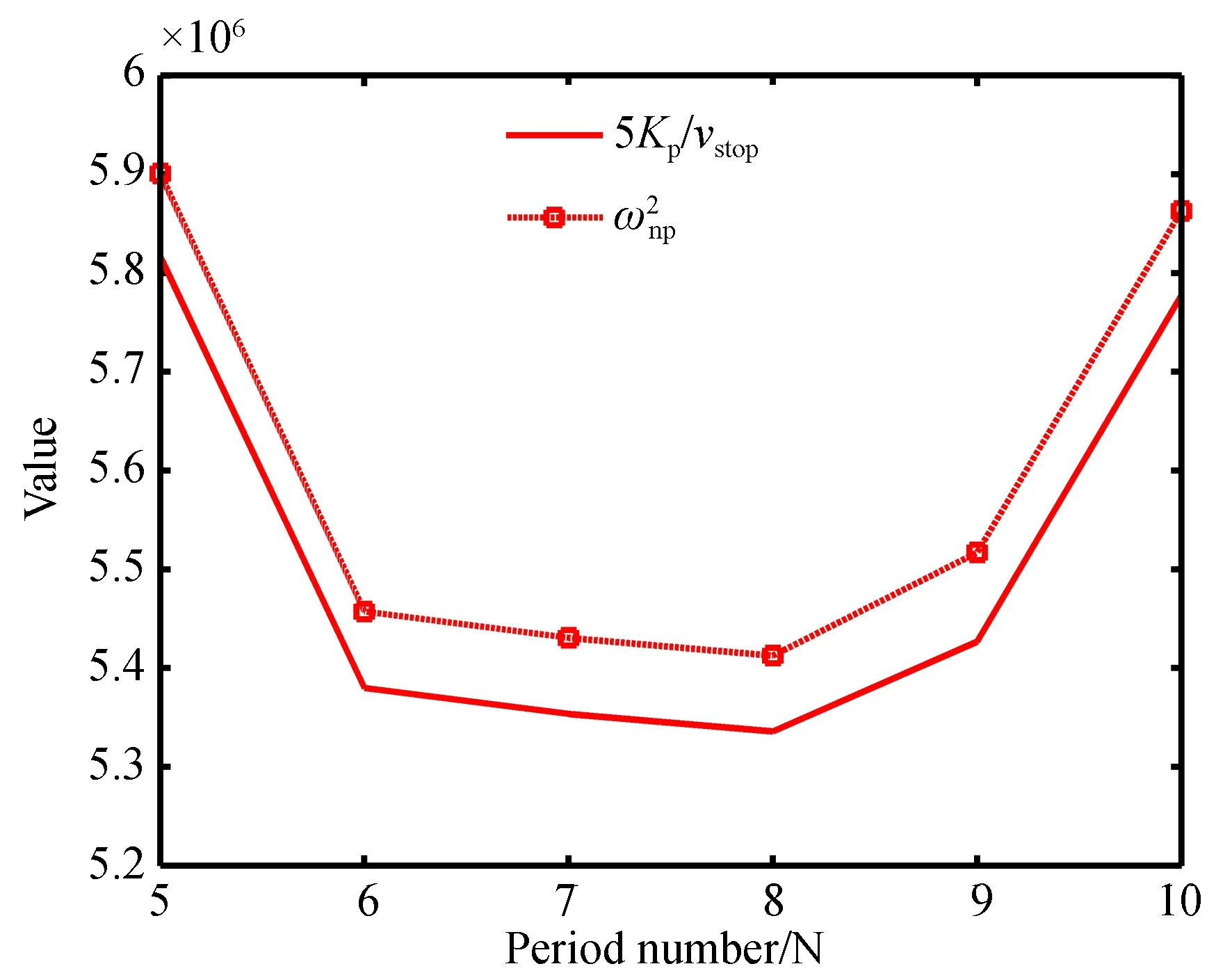
图12 5Kp/vstop与之间的数值关系Fig.12 Relationship between 5Kp/vstop and

(14)

联合关断点前后的辨识结果，通过式(5)进一步获得不同周期数的步进位移增量，和实验结果对比(图13)发现，辨识结果吻合度在85%以上，并且具有较好的一致性，说明所提出的两阶段二阶模型能够有效地预测超声电机周期数在10以内的步进运动规律。

图13 不同周期数的拟合结果Fig.13 Fitting results under different period numbers

4.2.2 高分辨率步进运动

依据步进量预测模型，控制激励电压幅值和频率分别为200 V和43 kHz，在周期数区间[1,10]内寻找运行稳定且定位可靠的参数使电机实现开环状态下的微步进运动。图14为周期数为2.1的步进曲线，由图可知，通过周期数的控制实现了3.3 μrad的步进量。从位移响应上看，不同时间片的运动在启动阶段的瞬时响应上存在一定的差异，有些阶段的超调量大，有些阶段的超调量小，但是在稳定阶段的表现则比较接近。

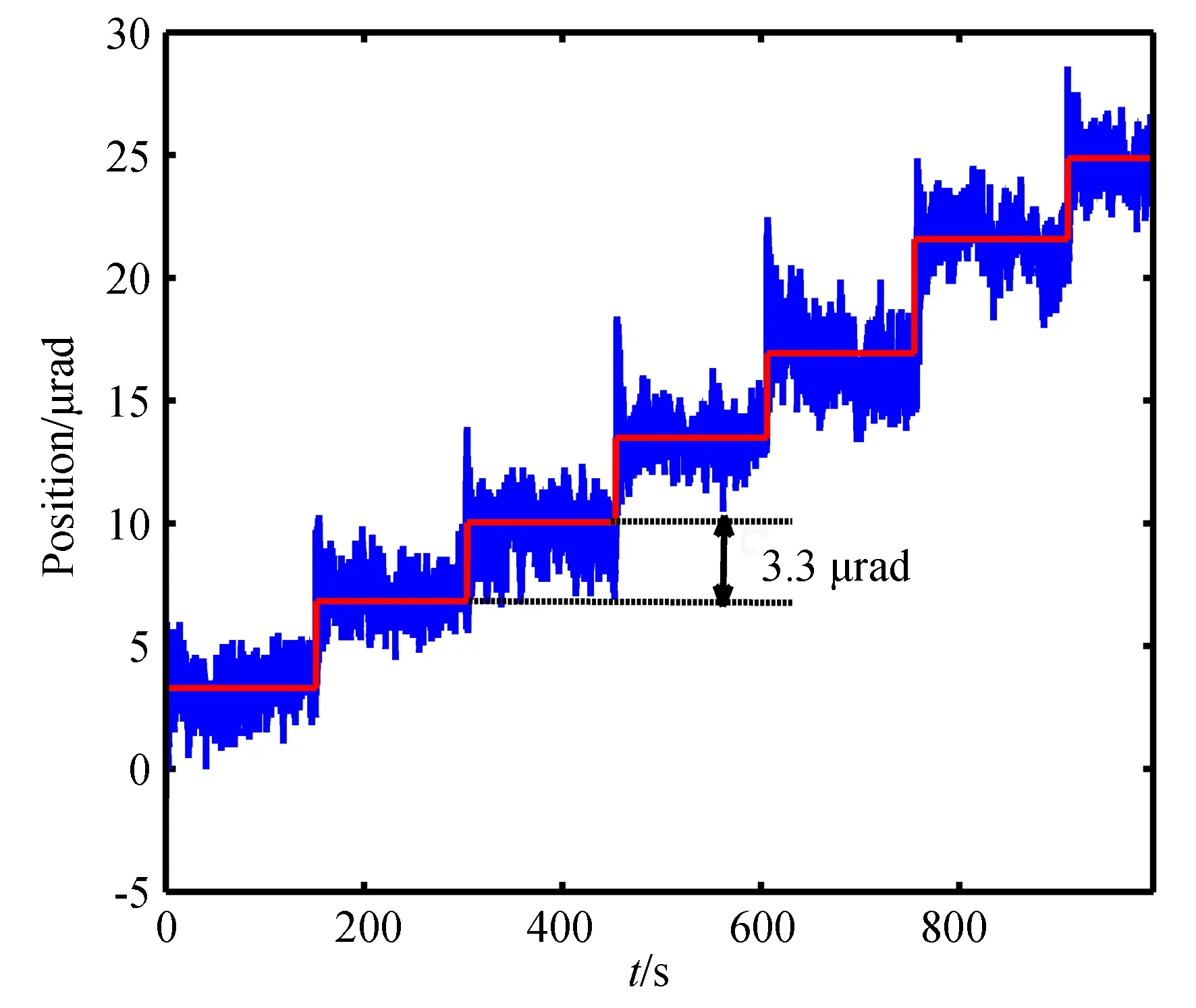
图14 施加周期数调控后的步进结果Fig.14 Stepwise curves under adjustment of period number

通过不同周期数步进状态的分析与整合，对超声电机所能达到的极限步进分辨率进行测试。设置驱动幅值为178 V，驱动频率为44.6 kHz，周期数为4.7，可以得到如图15所示的步进运动结果。由图可知，超声电机的步进运动可以达到现有编码器的极限分辨率，即0.375 μrad。

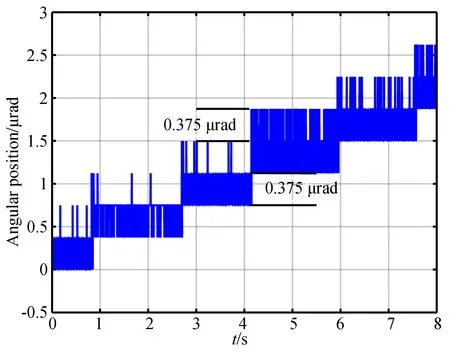
图15 开环步进位移曲线Fig.15 Open-loop stepwise position curve

4.2.3 角度定位控制

在传统的位置闭环控制中，当实际位置超过期望值需要解决速度换向时的突变问题,在增加控制系统复杂性的同时也会影响最终的位置精度。为解决这一问题，设计了一种分段逼近的控制方法。为了实现全局范围内的稳定运动，在以幅值为变化量，保持频率为44 kHz的基础上，具体的分段控制方法如下：当实际位置与指令位置之差大于10°时，速度指令为50 (°)/s；当差值大于5°小于10°时，速度指令为20 (°)/s；当差值大于0.1°小于5°时，速度指令为10 (°)/s；差值达到0.1°时，断开其中速度环，同时切换到步进运动模式，整个定位调整时间不超过1 s。

(15)

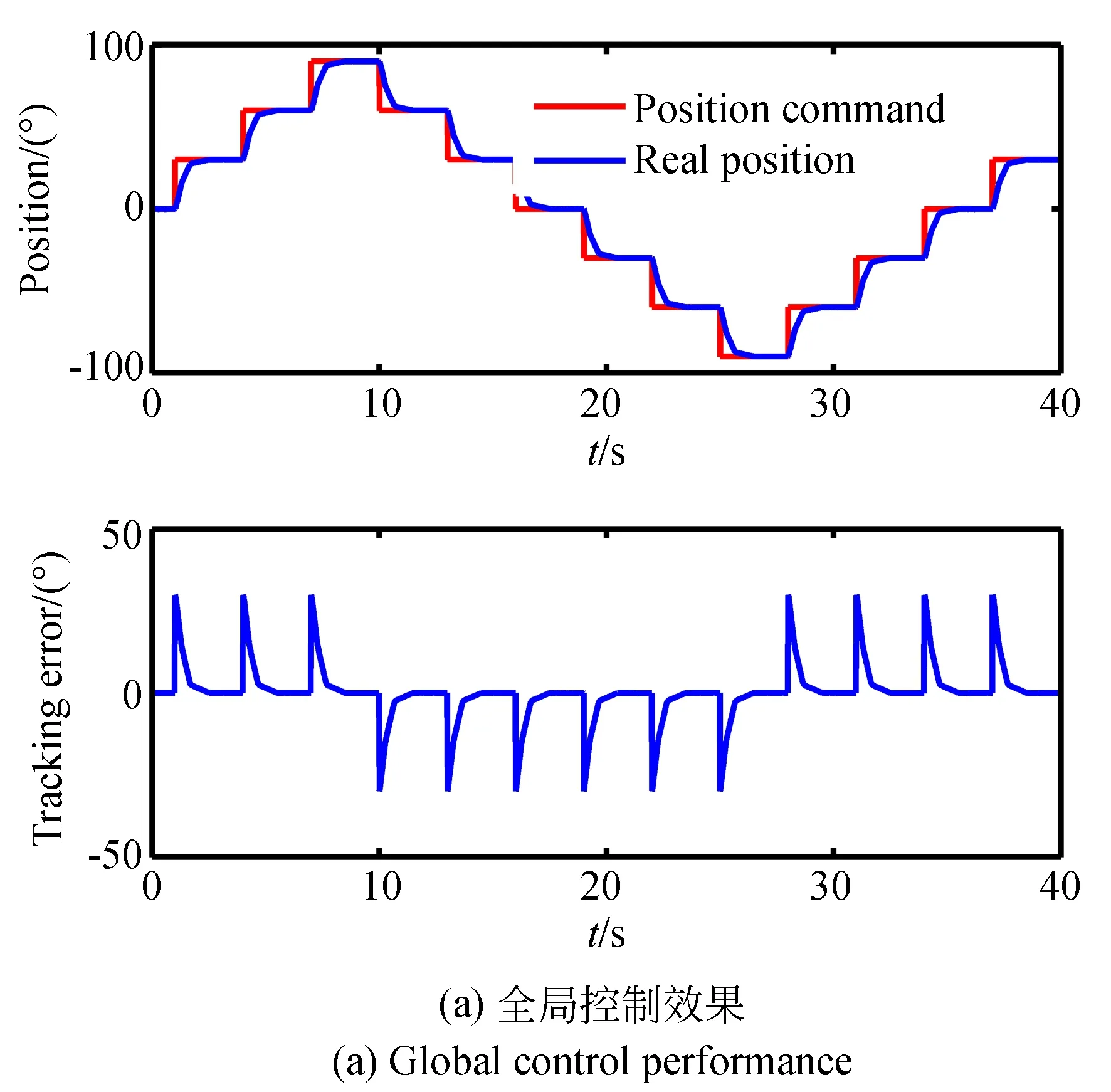
图16 电机定位控制效果Fig.16 Positioning control performances

5 结 论

针对超声电机不同的控制模式，本文提出了针对性的控制策略,在稳速控制上建立并辨识了多参数调速模型，采用“速度环+位置环”的双环控制策略使速度稳定性达到0.44%；在步进运动控制上，通过驱动参数调控与周期数控制实现了0.375 μrad的位置分辨率；在角度定位控制上，通过逐步逼近方法达到了1.7 μrad的定位精度。

本文充分发挥超声电机响应快，可定脉冲控制的优点，提出了有针对性的速度稳定性与位置分辨率控制策略，不仅能够保证控制精度，也能有效简化控制结构，对于推进压电驱动功能部件在高端装备的应用具有积极意义。