基于SURF特征描述符和杰卡德距离的文物碎片拼接

刘晓宁，狄宏璋，杨 稳，林芃樾，王世雄

(西北大学 信息科学与技术学院，陕西 西安 710127)

1 引 言

破碎文物的拼接在文物虚拟复原工作中的意义不言而喻,它是虚拟复原中至为关键的一步。由于信息技术的不断更新，文物的数字化虚拟拼接也不断有新的突破。目前文物的虚拟拼接技术大致可以分为断裂面受损和断裂面完整两种。

对于断裂面完整类文物，一般是采用基于断裂面轮廓线以及模型表面几何纹饰特征来进行匹配。比如刘军等[1]提出一种将断裂面几何特征与轮廓线特征相融合的拼接方法。袁洁[2]通过定义表面约束点来提取断裂面上的特征点,实现交互式文物拼接。赵夫群等[3]通过计算最长公共子序列实现断裂面的细匹配，从而确定其邻接关系。Schmid C等[4]提出一种高效的三维轮廓曲线来实现文物的拼接。

对于断裂面受损类文物，一般是从断裂面厚度出发，提取出鲁棒性能较好的断裂面显著特征来实现拼接。比如李珊珊[5]提出基于表面邻接约束并借助于领域专家先验知识的交互式文物拼接。袁洁等[6]提出基于Morse-smale拓扑特征的文物拼接算法，通过Morse-smale复形理论来构建断裂面的几何四边形拓扑图，计算4个顶点到基准面的高度差来构建拓扑图的特征描述符，来实现相似性检索。

目前现有的文物拼接算法，对于局部碎片缺失、数据量大的碎片模型，拼合效果不是特别的准确。因此，本文基于SURF(Speeded Up Robust Features)特征描述符和Jaccard距离来实现文物的精准拼接。首先采用Canny边缘检测算子[7-10]提取出文物模型周围的边沿线和表面几何纹饰线条，作为下一步特征提取的基础。其次,通过构造多尺度空间，在模型边缘线表面上提取出特征点，对其构造一系列具有强鲁棒性更显著的SURF特征点描述符[11-18]。然后,用Jaccard距离[19-22]计算特征点集相似度并筛选最优匹配点集，确定其邻接关系。最后，采用ICP(Iterative Closest Point)算法[23]多次迭代计算出刚体变化的参数,从而实现碎片拼接。实验表明在保证较精确拼接的同时，本文方法具有高效率、低冗余、强鲁棒等特点。

2 Canny边缘检测

2.1 边缘检测

对于三维模型来说，边缘是最直观、最能体现其几何纹饰信息的一种表示。Canny边缘检测满足以下要求:(1)检测出来的边缘线是基于人的视觉感受；(2)提取出来的边缘线不会影响模型表面的纹饰特征；(3)边缘线较细，并且无缝连接，不会出现局部断开。所以本文用Canny算子提取碎片模型边缘线。

2.2 高斯滤波平滑图像

首先，进行模型预处理操作,消除噪声等因素对文物边缘线检测产生的影响。高斯滤波器计算如公式(1)：

i≤2k+1,j≤2k+1，

(1)

然后要与8邻域像素矩阵做卷积运算，为了计算的高效性与实效性，故令k=1,ε=1.2,经过数据归一化后的高斯滤波器H如公式(2)所示:

(2)

设模型中某一点像素值为e，其8邻域像素值矩阵为B。将其与3×3的高斯滤波器模板的中心位置对齐从而进行卷积操作，即将该像素点8邻域乘积权值叠加，作为该点高斯模糊后的亮度值w。则有:

(3)

2.3 边缘梯度检测

由于碎片原始模型大多纹理丰富、特征复杂，若在其上直接提取特征点会导致特征点集不够泛化，无法更进一步匹配。因此，用Canny算子检测出其水平、垂直以及斜对角线方向的边缘线。Canny算子x方向和y方向的3×3模板分别为:

(4)

梯度计算公式如式(5)所示，H代表计算得到的梯度值，θ代表其梯度方向。

(5)

2.4 边缘线生成

生成的边缘线要最大程度反应碎片的边缘信息和表面纹饰特征，即先进一步缩小范围确定当前局部区域内最优点，对任一像素点P,若其梯度值大于我们设定的高阈值，则认为P为强边缘像素，将其保留并纳入边缘像素点集合M={mi|i=1,2,3,...,n}。若其梯度值大于低阈值并且小于高阈值，则认为其为弱边缘像素，再去观察其8邻接像素点梯度值，若存在梯度值大于高阈值的像素，则将其也纳入到边缘像素点集合M里，否则将其删除。若任一像素点的梯度值小于低阈值，则直接将其删除。其伪代码描述如下:

Algorithm: Progress of picking up four-element pixel1 Input: P: One of a pixel;2Hthreshold: high threshold;3Lthreshold: low threshold;4 Output: P is edge pixel or not;5 if P>hthreshold then6 P must be on edge7 end if8 else if P>Lthreshold and P>Hthreshold then9 for each ∑p' do10 if p' Hthreshold then11 P must be an edge

12 break13 end if14 end for15 end if16 else17 P must be renamed

其中，P代表当前像素点，Hthreshold=0.8,Lthreshold=0.4分别为设定的高低阈值，它是通过多次实验计算得出，当高阈值与低阈值的比值为2∶1时，提取出的边缘线效果更优。

该算法提取的模型边缘线更加符合人类视觉观感，可以清晰的表示模型表面几何纹饰特征以及边缘轮廓信息，为下一步碎片特征点提取打下了良好的基础，如图1所示分别C2-4-065，C2-4-064，C2-4-033号碎片模型及其对应的边缘线图。

图1 模型边缘线提取Fig.1 Model edge line extraction

3 特征提取

提取碎片显著特征点大都是通过曲率、极大值及极小值的计算来确定。本文结合以往先验知识，通过构造多尺度空间使提取出来的特征点更加泛化，具有一般性。其主要步骤如下:

Step 1.构造多尺度空间。为了更进一步缩小特征点的范围，使ε分别取值为1.1、1.3、1.4，得到的高斯滤波器分别为h1,h2和h3，如公式(6)所示。将高斯滤波器与碎片模型卷积操作会得到不同尺度空间下的模型。

(6)

Step 2.空间特征点检测。为了保证关键点的尺度不变性以及高鲁棒性,需要对模型邻域和尺度空间邻域点进行大小比较。如下图所示,取中间的检测点p和其邻域8个点进行大小比较。在其尺度空间内,和其上下邻域共18个检测点进行大小比较。若检测点p在其邻域和空间邻域内是最大值或最小值,就认为点p为候选特征点。

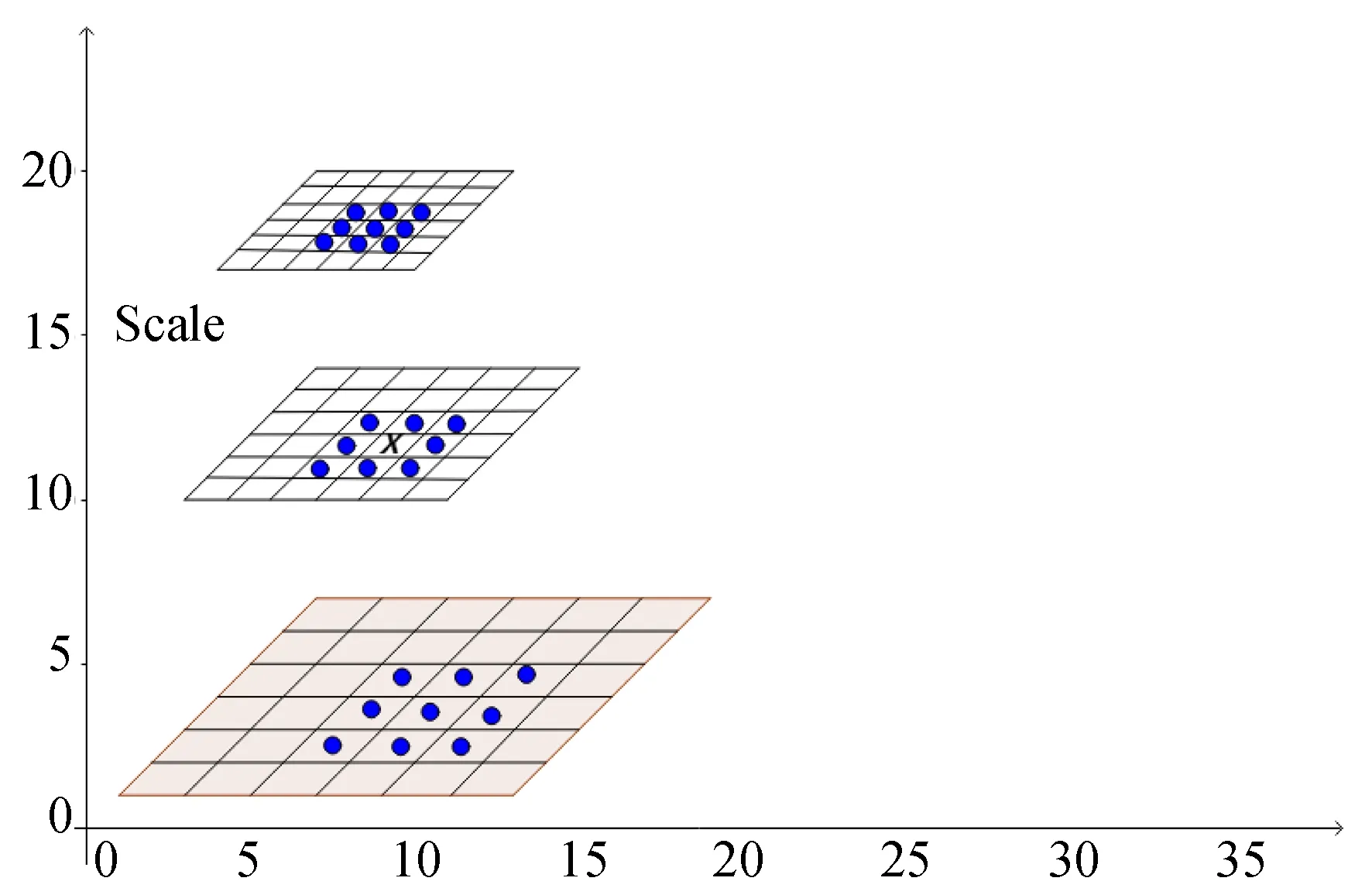
图2 不同尺度空间的图像Fig.2 Images in different scale spaces

Step 3.特征点精确定位。Step2中得到的特征点其实是属于多尺度空间中候选特征点，其具有不稳定性与发散性，并不一定是真实的特征点。还需要对其进行曲线拟合来使其线性化,精确的确定特征点的位置，剔除掉低分辨率的特征点,增强匹配的稳定性与完整性。

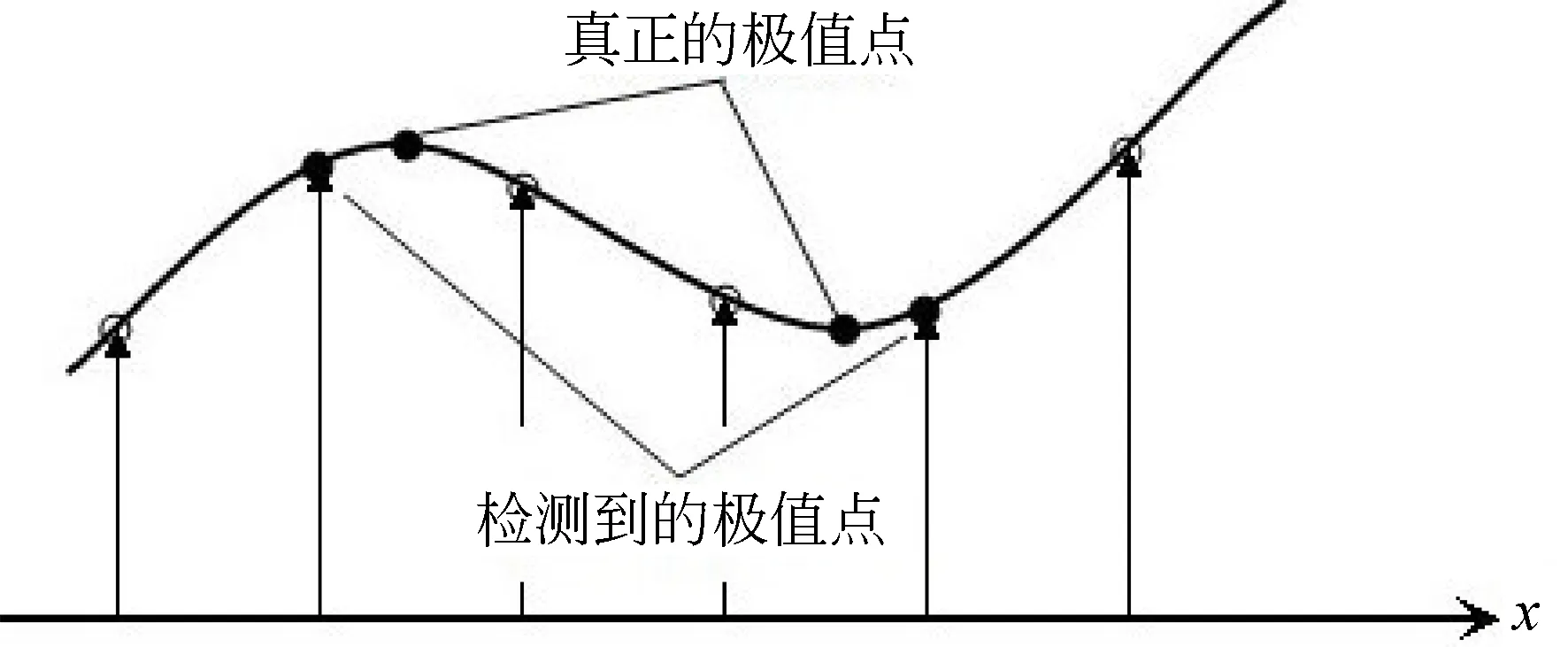
图3 特征点定位Fig.3 Feature point positioning

这里曲线拟合函数的展开式为:

(7)

对其求导取0，得到:

(8)

将该值代入展开式里得到:

(9)

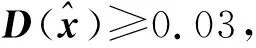
4 构建SURF特征描述符

构建特征描述符大都以断面特征点为基础，这样如果提取的特征点存在误差，也会导致特征描述符失真。本文基于SURF特征描述符的鲁棒性与一般性，构建出不仅包括该特征点的相关信息,还会包含其邻域范围内有较强光谱映射的特征点信息的SURF特征描述符。

图4 构建特征描述符Fig.4 Construct feature description factor

如图4中心红点Q为所选择的特征点，以Q为中心点结合直方图映射构造一个4×4模板，在这个模板内每一小块都认为是点Q的一个邻域生长点(彩图见期刊电子版)。箭头方向表示每个邻域生长点的8个梯度方向。再用卷积核与每一块进行卷积加权运算,可得到每个邻域生长点的8个梯度描述符。故对于任一特征点Q来说,其特征描述符可以用4×4×8维的梯度描述向量W来表示,W=(w1,w2,w3,....,w128)。在对其进行归一化得到L=(l1,l2,...,l128)。归一化公式如式(10):

(10)

5 相似性匹配

由于碎片模型拓扑特征的复杂性以及特征点的多维度特性,若用欧氏距离计算特征点集的匹配关系,其运算结果时间复杂度会特别的高并且会存在一定的误差。基于此,为了对待拼接文物碎片断裂面及模型表面纹饰特征点的相似型进行精确检测,本文采用Jaccard距离来构造最优特征点匹配集合,从而确定其邻接关系,大大提高了匹配检测的效率。其步骤如下:

Step 1.构建Jaccard系数∂。设碎片SA和碎片SB的特征点集合分别为A和B：

A={Ai|i=1,2,...,n}

B={Bj|j=1,2,...,k}

(11)

其中：∩表示特征点集合A与B的交集,∪表示特征点集合A与B的并集。

Step 2.构建Jaccard距离d。其公式为:

(12)

对碎片SA中任一特征点Ai,遍历碎片SB的特征点集合B,若存在特征点Bj满足Jaccard距离d(Ai,Bj)<∂,则将(j=1,2,...,n)纳入匹配集合Q内。此时还不是最优,因为在B中会存在多个特征点。所以需要遍历匹配集合Q，找出满足Jaccard距离最小的特征点Bj,从而构成最佳匹配组。

6 刚体拼合

经过上述操作,已经得到了待拼接碎片间最优匹配特征点集合H={〈SAi,SBi〉|i=1,2,...,n}。这一步主要是将位于不同坐标系下的特征点集,转化为同一坐标系下,来完成文物碎片的准确拼接。本文采用ICP算法来求解旋转矩阵R和平移矩阵T，从而实现碎片模型的刚体变化。主要步骤如下:

Step 1:从最优匹配特征点集合中任意选取两组不共线的特征点对〈SAj,SBj〉〈SAk,SBk〉(j,k∈[1,n],j≠k)。利用ICP算法计算出旋转矩阵R和平移矩阵T,将其保存在刚体变化数组V[m]中。

Step 2:经过上述操作得到m个刚体变化参数,则刚体变化数组记为V[m]={v0,v1,v2，...,vm},其中v[i]={(Ri,Ti)|i∈[0,m]}。

Step 3: 遍历刚体变化数组V[m],将其代入目标函数求解。则求解最优变化参数R和T就可以转化为求满足目标函数W最小值的最优解问题。

(13)

Step 4:求解得到最优参数R和T,完成碎片的精确拼接。

7 实验结果及分析

本实验采用VicualC++和Open CV编程,在Intel i7-6700k CPU/4.0 GHz,32 G内存的PC机上实现。以1号坑的C2-4号121块右骖马碎片模型作为实验数据。

图5 C2-4号右骖马发掘现场图Fig.5 Excavation site of No. C2-4

7.1 重组实验结果

图5所示为采用本文算法对c2-4号右骖马碎片重组后的效果图，分别为右视图、左视图、正视图及其对应的边缘线图与提取出的三维特征点云图。拼合时间如表1所示,其中n表示碎片块数,t1表示提取模型边缘线所需的时间,t2表示确定碎片及周边碎片的几何邻接关系所需的时间,t3表示碎片重组拼接需要的时间。

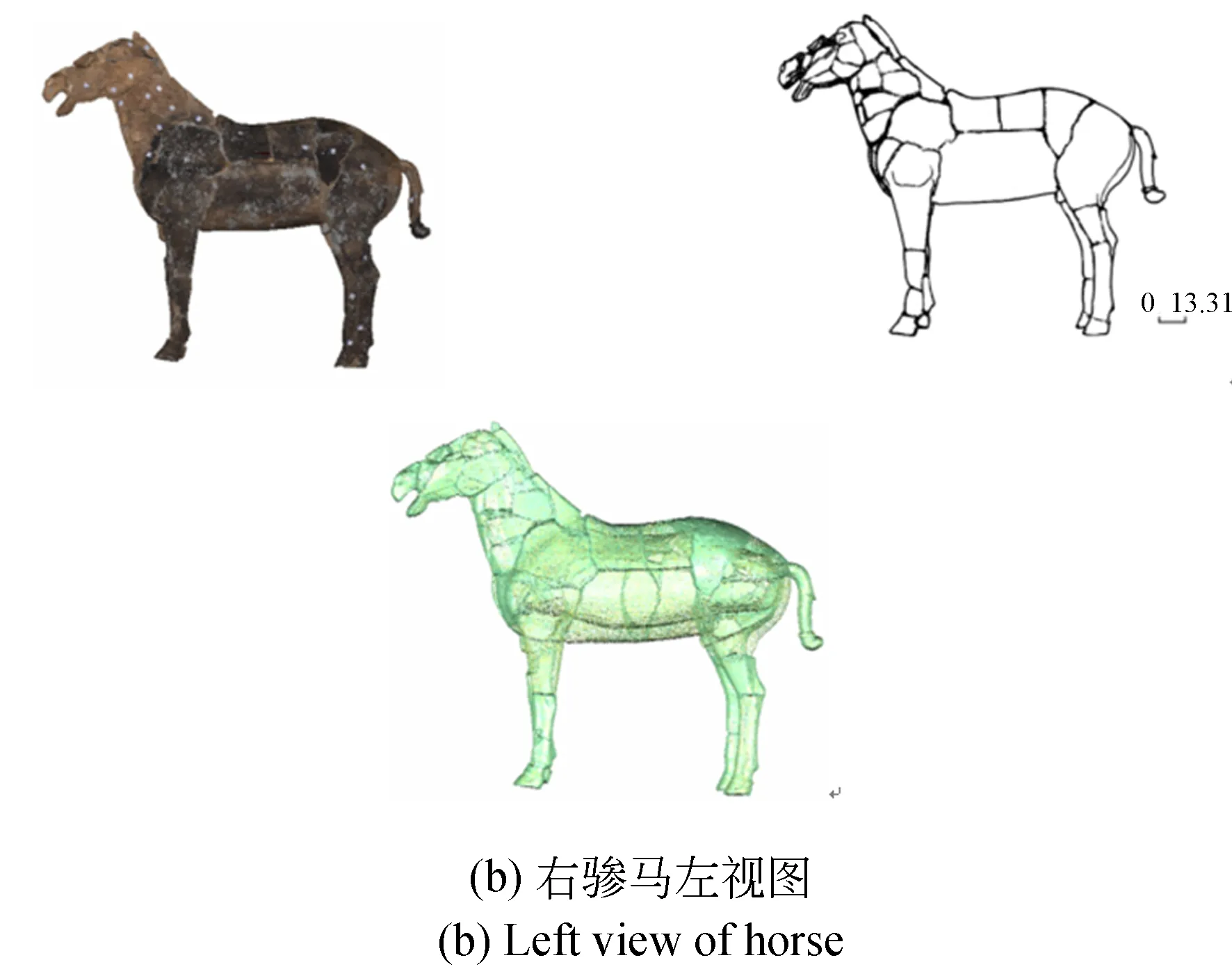
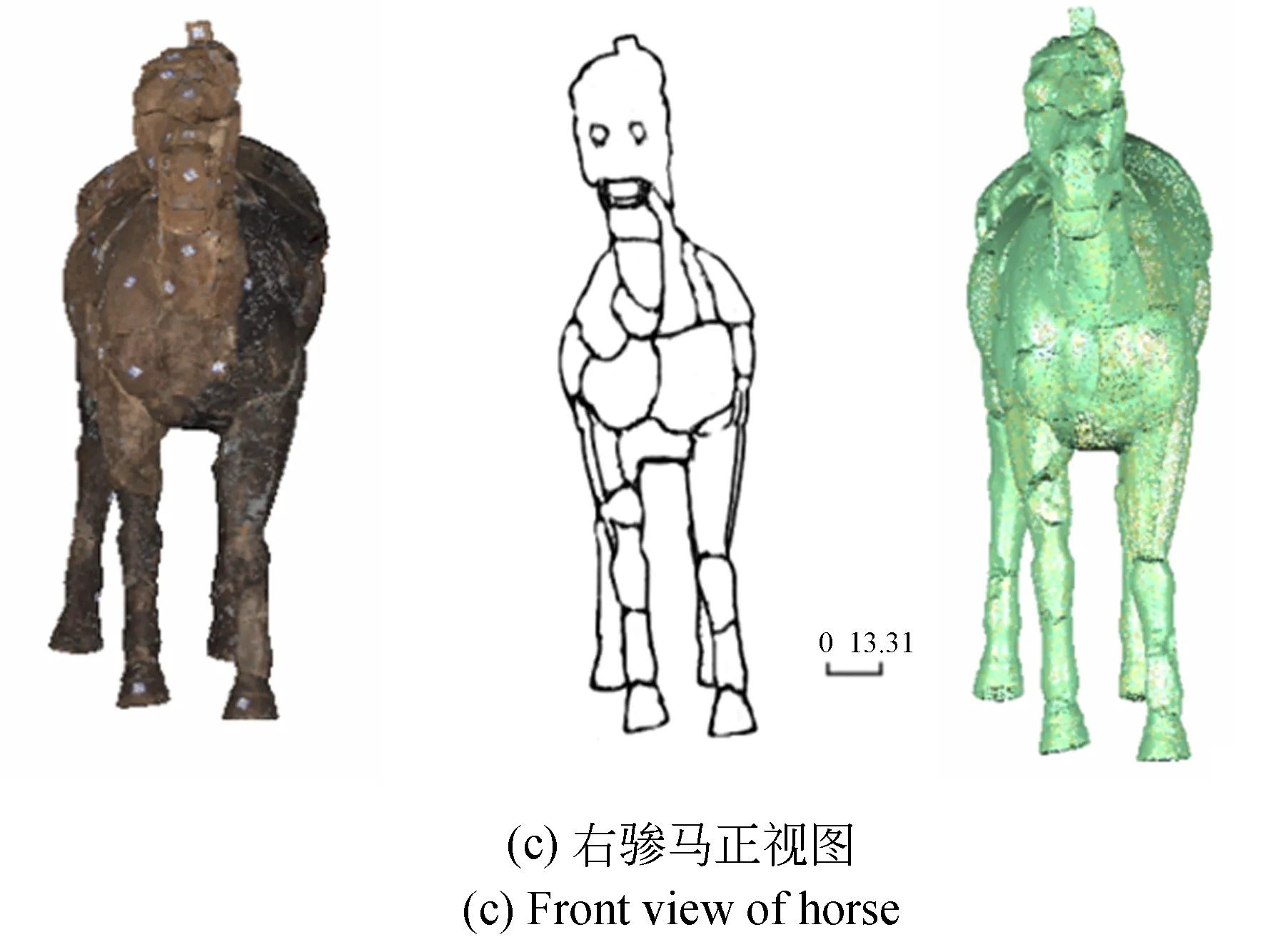
图6 右骖马三视图Fig.6 Three views of horse

表1 右骖马拼接所需时间

Tab.1 Splicing time required for horse

n t1/s t2/st3/s12170.34657.44223.212

7.2 局部拼接实验结果

图6所示分别为C2-4-064,C2-4-063和C2-4-033号碎片及其拼接关系图，其位置如图蓝色标注处(彩图见期刊电子版)，直线标明的是其周边邻接碎片的位置。可以看到即使存在部分断裂面受损的碎片，采用本文方法也能较准确地定位出其邻接位置，取得较好的拼合效果。

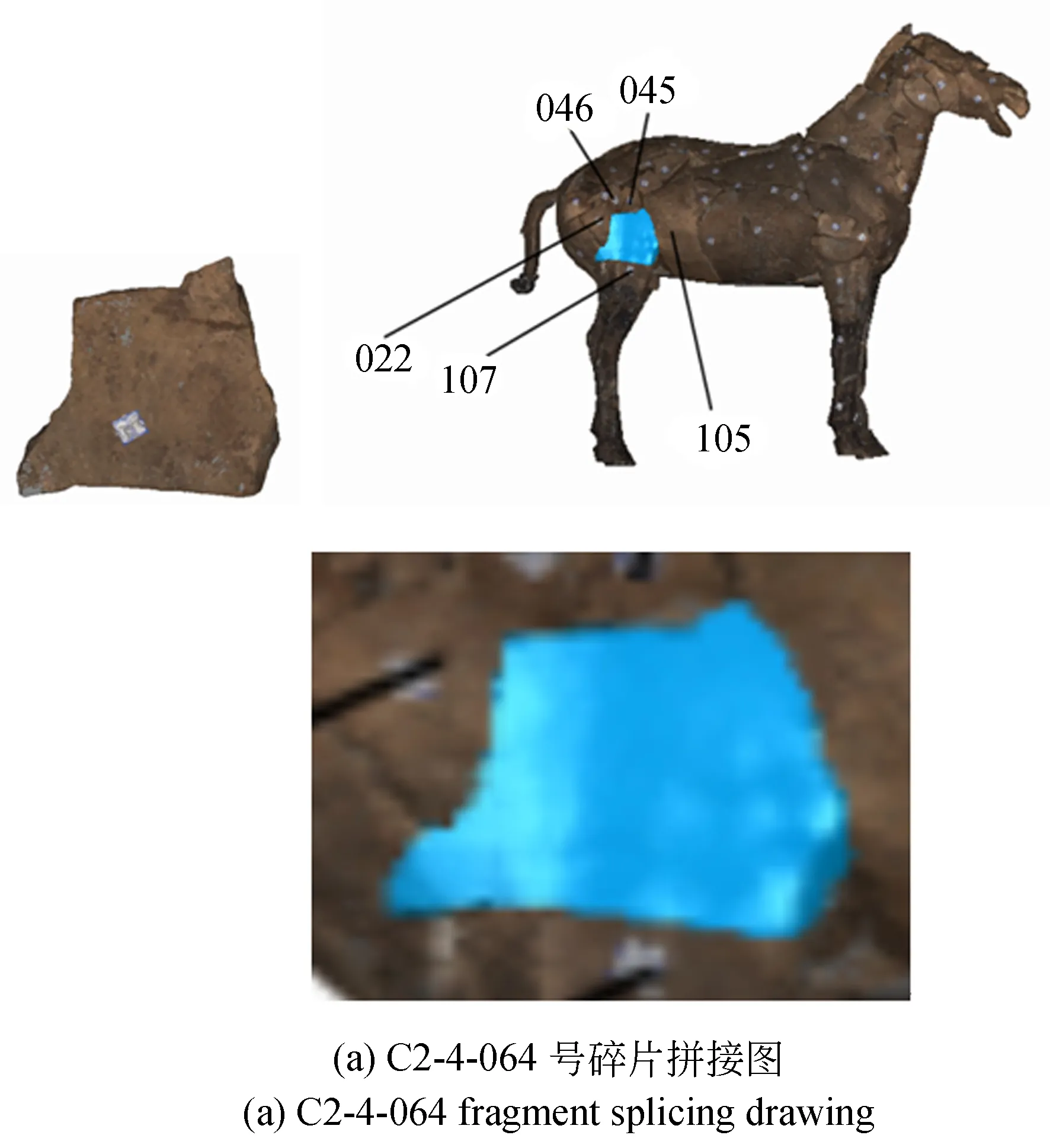
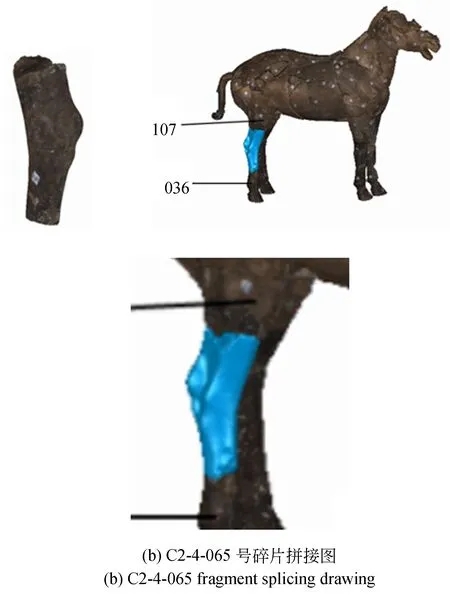
图7 拼接关系图Fig.7 Splicing diagram

7.3 对比实验结果

图7(a)为采用本文方法对C2-4-18(蓝色标注处)号碎片进行拼接的效果。图7(b)为用文献[22]方法的拼接效果图(红色标注处，彩图见期刊电子版)，可以看到其几何特征无法正确的反映出其邻接关系，呈现出浸透现象，如黑色方框所标注。

图8 C2-4-18号碎片拼接效果图Fig.8 No.C2-4-18 effect drawing of fragment splicing

图9 C2-4-13号碎片拼接效果图Fig.9 No.C2-4-18 effect drawing of fragment splicing

图8(a)为采用本文方法对C2-4-13号碎片(蓝色标注处)进行拼接的效果。图8(b)为用文献[18]方法的拼接效果图(红色标注处，彩图见期刊电子版)，可以看到存在明显的缝隙过大现象，如黑色圆圈标注处所示。

表2所示为本文算法与文献[18]、文献[22]算法的运行时间和拼合误差对比，拼合误差为邻接碎片断裂面轮廓线上特征点集间的欧式距离之和的平均值。本文算法的运行时间与文献[18]相比提高了16%，与文献[22]相比提高了12%。拼合误差相对于文献[18]和文献[22]来说更小，不超过0.750 mm，拼合效果更准确，适用于断裂面受损的碎片拼接。

表2 运行时间与拼合误差对比

8 结 论

本文主要针对文物多碎片拼接过程中出现的局部碎片缺失、纹饰几何特征点受损而不能准确提取断裂面纹饰特征等严重问题，提出基于SURF特征描述符和Jaccard距离的碎片拼接方法。先用Canny算子提取出碎片模型中能够表示其几何纹饰特征的边缘线，从而进一步简化其几何模型。再构造多Scale空间来提取碎片模型断裂面的特征点，构建SURF特征描述子。利用特征点集间的邻接几何特性，不同于欧式距离计算的高复杂度与低时性，本文用Jaccard距离计算特征点集相似度。实验结果表明，本文方法使得拼合误差减少到0.750 mm内，算法运行时间与文献[18]和文献[22]相比分别提高了12%和16%，可以有效地减少因断裂面破损而造成的拼接缝隙过大、出现渗透等现象。

由于构建特征描述符的维数比较大，因此寻找更加鲁棒、高效的特征描述符将是下一步着重的研究方向。