基于粒度矩阵的程度多粒度粗糙集粒度约简

汪小燕, 申元霞

(安徽工业大学计算机科学与技术学院, 安徽 马鞍山 243032)



基于粒度矩阵的程度多粒度粗糙集粒度约简

汪小燕, 申元霞

(安徽工业大学计算机科学与技术学院, 安徽 马鞍山 243032)

多粒度是粗糙集理论中的一种有效的数据处理方法,粒度约简是获取信息系统简洁规则的前提。研究了程度乐(悲)观多粒度粗糙集粒度约简理论,改进了程度粗糙集的下近似定义,提出了程度多粒度粗糙集的粒度矩阵。基于粒度矩阵,研究了程度多粒度粗糙集下近似计算理论和粒度的必要性,提出程度乐观多粒度粗糙集核粒度的定义。针对程度乐(悲)观多粒度粗糙集,提出基于粒度矩阵的粒度约简方法。最后利用实例分析验证了所提粒度约简方法的正确性。

程度多粒度粗糙集; 粒度矩阵; 核粒度; 粒度约简

0 引 言

Pawlak粗糙集是从整体上对所有条件属性集合或决策属性集合,依据等价关系,将论域划分形成条件属性类或决策属性类。文献[1-5]分析研究了Pawlak粗糙集整体划分构成单个粒度空间的不足,提出了多粒度粗糙集模型。根据下近似条件宽松与严格,定义了乐(悲)观多粒度粗糙集模型。多粒度粗糙集将条件属性划分成多个粒度,每个粒度分别对论域划分,形成多个粒度空间。应用到实际决策问题时,依据多个粒空间获得的知识对比Pawlak粗糙集的单一知识更加合理。一些学者在集值信息系统[6]、序信息系统[7]、不完备信息系统[8]、邻域关系[9]、模糊关系[10]等方面对多粒度粗糙集做出了不同角度的扩展。多粒度粗糙集中的粒度约简是在不影响信息系统决策前提下,删除对获取知识没有意义的粒度。粒度约简对获取简洁、有效的决策规则具有重要意义。因此,一些学者深入研究了多粒度粗糙集中的粒度约简,提出不同的方法。针对悲观多粒度粗糙集,文献[11-13]分别提出了下近似分布约简、基于信息量的下近似分布约简方法和基于重要度的上(下)近似分布约简方法。文献[14]提出了可变多粒度粗糙集粒度约简方法。目前的多粒度粗糙集的粒度约简主要是基于悲观多粒度粗糙集,利用粒度重要性进行约简的。本文利用程度多粒度粗糙集模型,提出程度多粒度粗糙集粒度矩阵,结合粒度矩阵提出一种简单有效的粒度约简方法。

1 相关概念

Pawlak粗糙集计算下近似要求集合间必须是完全包含关系,不考虑一定程度上的“包含”,当集合间没有完全包含关系,却具有对分类重要的重叠信息时,应当考虑一定程度的包含。在这种背景下,文献[15]提出了程度粗糙集。

定义 1[15]设信息系统S,属性子集A1,A2,…,Am⊆AT,k为非负常数,∀X⊆U,X关于A,依据程度k的下、上近似分别定义为

(1)

(2)

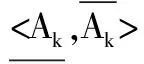
在程度粗糙集中应用多粒度知识,文献[16] 分别从乐观和悲观方面提出两种程度多粒度粗糙集。

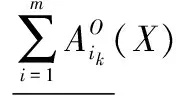
|[x]Am|-|[x]Am∩X|≤k}

(3)

(4)

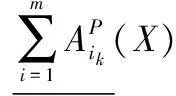
|[x]Am∩X|≤k}

(5)

(6)

2 粒度矩阵

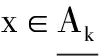
定义 4 设信息系统S=对于∀X⊆U,A⊆AT,k为非负常数,X的程度粗糙集下近似为

k∧[x]A∩X≠φ}

(7)

定理 1 设信息系统S=,对于∀X⊆U,A⊆AT,k为非负常数,X的程度粗糙集下近似和上近似分别为

φ}

式中,[x]A-X表示集合X相对于集合[x]A的补集。

证明 由定义1,定义4和集合的相对补集、绝对补运算可得证。

证毕

定义 7 设S=是一个信息系统,其中A1,A2,…,Am⊆AT,D为决策属性,k为非负常数,A={A1,A2,…,Am},U/D={Y1,Y2,…,Yn},则程度多粒度粗糙集粒度矩阵M={mij}定义为

(8)

粒度矩阵包含|U|行, |U/D|列, |U|表示信息系统中实例数, |U/D|表示决策属性类数,粒度矩阵中的非空元素mij是满足|[xi]B-Yj|≤k∧[xi]B∩Yj≠φ的条件属性粒度B组成的集合。

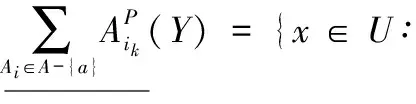
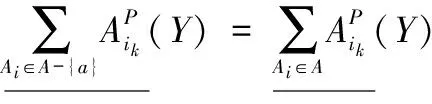
定理 2 程度多粒度粗糙集粒度矩阵M={mij}中,A是所有条件属性粒度集合,a∈A,对∀Y∈U/D,若∀Y∈U/D列不存在只包含粒度集合A-{a}中所有粒度的元素,则在程度悲观多粒度粗糙集中粒度a在粒度集合A中是不必要的,否则称粒度a在粒度集合A中是必要的。

证明 由定义5和推论4可证。

证毕

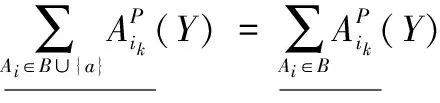
定理 3 程度多粒度粗糙集粒度矩阵M={mij}中,A是所有条件属性粒度集合,B⊂A,a∈A-B,对∀Y∈U/D,若∀Y∈U/D列所有包含粒度集合B中所有粒度的元素,同时也包含粒度a,则在程度悲观多粒度粗糙集中粒度a对粒度集合B是不必要的;否则,称粒度a对粒度集合B是必要的。

证明 由定义6和推论5可证。

证毕

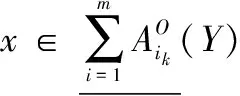
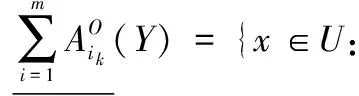
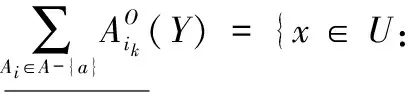
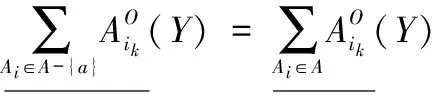
定理 4 程度多粒度粗糙集粒度矩阵M={mij}中,A是所有条件属性粒度集合,a∈A,对∀Y∈U/D,若∀Y∈U/D列不存在只包含粒度a的元素,则在程度乐观多粒度粗糙集中粒度a在粒度集合A中是不必要的;否则,称粒度a在粒度集合A中是必要的。

证明 由定义5和推论9可证。

证毕

定理 5 程度多粒度粗糙集粒度矩阵M={mij}中,A是所有条件属性粒度集合,B⊂A,a∈A-B,对∀Y∈U/D,若∀Y∈U/D列不存在包含粒度a且不包含粒度集合B中任意粒度的元素,则在程度乐观多粒度粗糙集中粒度a对粒度集合B是不必要的,否则称粒度a对粒度集合B是必要的。

证明 由定义6和推论10可证。

证毕

定义 8 程度多粒度粗糙集粒度矩阵M={mij}中,A是所有条件属性粒度集合,若某个对象x∈U与某个决策类∀Y∈U/D所对应的元素只包含一个唯一粒度Ai∈A,则Ai为程度乐观多粒度粗糙集的核粒度。

3 粒度约简

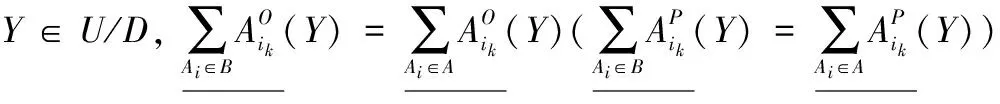
定理 6 在粒度矩阵M中,A是所有条件属性粒度集合,T={mij|mij为粒度矩阵中所有不为∅的元素},若red⊂A,且∀mij∈T,red∩mij≠∅,而对∀red′⊂red,存在red′∩mij=∅,则集合red为程度乐观多粒度粗糙集的下近似分布粒度约简。

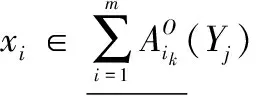
证毕

程度乐观多粒度粗糙集的粒度约简算法步骤描述如下。

输入 决策信息系统S=,A1,A2,…,Am⊆AT为条件属性粒度,A={A1,A2,…,Am},U/D={Y1,Y2,…,Yn}。

输出 决策信息系统的一个程度乐观多粒度粗糙集的粒度约简red。

步骤 1 根据定义7建立粒度矩阵M={mij}。

步骤 2 将粒度矩阵中的核粒度加入到red中。

步骤 3 将粒度矩阵中的包含集合red中任意粒度的元素改为∅。

步骤 4 若粒度矩阵中的所有元素都为∅,则转步骤6;否则转步骤5。

步骤 5 将粒度矩阵中不为∅的元素中选择一粒度加入到集合red中,转步骤3。

步骤 6 输出粒度约简集red。

在程度乐观多粒度粗糙集粒度约简算法中,计算各个粒度对论域划分的时间复杂度为O(m|U|2),建立粒度矩阵的时间复杂度为O(mn|U|),在最坏情况下利用粒度矩阵获得粒度约简的时间复杂度为O(mn|U|)。在决策信息系统中,一般对象的个数大于决策属性分类数,所以该算法需要的时间复杂度为O(m|U|2)。粒度矩阵的空间复杂度为O(n|U|)。

定理 7 在粒度矩阵M中,A是所有条件属性粒度集合,T={mij|mij⊂A且mij≠∅},若red⊂A,且∀mij∈T,red-mij≠∅,而对∀red′⊂red,存在red′-mij=∅,则集合red为程度悲观多粒度粗糙集的下近似分布粒度约简。

证毕

针对程度悲观多粒度粗糙集,给出基于粒度矩阵的粒度约简算法步骤如下。

输入 决策信息系统为S=,A1,A2,…,Am⊆AT为条件属性粒度,A={A1,A2,…,Am},U/D={Y1,Y2,…,Yn},T=∅。

输出 决策信息系统的一个程度悲观多粒度粗糙集的粒度约简red。

步骤 1 根据定义7建立粒度矩阵M={mij}。

步骤 2 将粒度矩阵中的mij⊂A且mij≠∅的元素加入到集合T中。

步骤 3 选择必要粒度加入到集合red中。

步骤 4 将集合T中所有满足red-mij≠∅的元素删除。

步骤 5 如果T=∅,则转步骤7；否则,转步骤6。

步骤 6 在A-red中选择一粒度加入到集合red中,转步骤4。

步骤 7 输出粒度约简集red。

在程度悲观多粒度粗糙集粒度约简算法中,计算每个粒度划分论域的时间复杂度为O(m|U|2),建立程度多粒度粗糙集粒度矩阵的时间复杂度为O(mn|U|),计算所有必要性粒度的时间复杂度为O(m2n|U|)。所以,该算法需要的时间复杂度为O(m|U|2+m2n|U|)。

4 实例分析

例 1 设决策系统S=,其中对象集U={x1,x2,…,x9},条件属性为a1,a2,a3,a4,d为决策属性,如表1所示。令条件属性粒度集A={A1,A2,A3}={{a1,a2},{a2,a3},{a3,a4}},取k=1。U/IND(d)={D1,D2}={{x2,x4,x6,x8},{x1,x3,x5,x7,x9}}

建立程度多粒度粗糙集粒度矩阵如表2所示。

表1 决策信息表

表2 粒度矩阵表

(1) 计算程度乐观多粒度粗糙集粒度约简

核粒度为A2,将粒度矩阵中的包含A2的元素改为∅后,只有m52={A1A3}≠∅,所以最终获得的粒度约简为{A1,A2}或{A2,A3}。

(2) 计算程度悲观多粒度粗糙集粒度约简

5 结 论

本文针对程度多粒度粗糙集,定义了粒度矩阵,围绕粒度矩阵,研究了程度多粒度粗糙集的相关理论。粒度矩阵可以方便计算程度乐(悲)观多粒度粗糙集的上、下近似。给出程度乐观多粒度粗糙集核粒度定义,提出了基于粒度矩阵的程度多粒度粗糙集粒度约简算法。在提取核粒度(或必要粒度)的基础上,可快速计算出程度乐(悲)观多粒度粗糙集的下近似约简。下一步的研究工作是对粒度约简后的信息系统进行规则提取研究。

[1] Qian Y H, Liang J Y. Rough set method based on multigranulations[C]∥Proc.ofthe5thIEEEInternationalConferenceonCognitiveInformatics, 2006:297-304.

[2] Qian Y H,Liang J Y,Wei W.Pessimistic rough decision[C]∥Proc.ofthe2ndInternationalWorkshoponRoughSetsTheory, 2010: 440-449.

[3] Qian Y H, Liang J Y,Yao Y Y, et al. MGRS: A multi-granulation rough set[J].InformationSciences, 2010,180(6): 949-970.

[4] Qian Y H, Liang J Y, Dang C Y. Incomplete multi-granulation rough set[J].IEEETrans.onSystems,Man,andCybernetics-PartA:SystemsandHumans, 2010, 40(2): 420-431.

[5] Qian Y H, Zhang H, Sang Y L, et al. Multigranulation decision-theoretic rough sets[J].InternationalJournalofApproximateReasoning, 2014, 55(1): 225-237.

[6] Ma R, Liu W Q. Multi-granulation rough set model based on set-valued information system[J].SystemsEngineeringandElectronics, 2014, 36(5): 920-925.(马睿,刘文奇. 基于集值信息系统的多粒度粗糙集[J].系统工程与电子技术, 2014, 36(5): 920-925.)

[7] Sun W X, Zhuo C Y, Wang G D, et al. Generalized multi-granulation rough set in ordered information system[J].JournalofFrontiersofComputerScienceandTechnology, 2015,9(3):376-384. (孙文鑫,卓春英,王国栋,等. 序信息系统的一般多粒度粗糙集[J].计算机科学与探索, 2015, 9(3): 376-384)

[8] Zhang M, Tang Z M, Xu W Y, et al. Incomplete variable multi-granulation rough sets decision[J].AppliedMathematics&InformationScience, 2014, 8(3):1159-1166.

[9] Lin G P, Qian Y H, Li J J. NMGRS: neighborhood-based multi-granulation rough sets[J].InternationalJournalofApproximateReasoning, 2012, 53(7): 1080-1093.

[10] Lin G P, Liang J Y, Qian Y H, et al. A fuzzy multi-granulation decision theoretic approach to multi-source fuzzy information systems[J].Knowledge-BasedSystems, 2016, 91(C): 102-113.

[11] Sang Y L, Qian Y H. A granular space reduction approach to pessimistic multi-granulation rough sets[J].PatternRecognitionandArtificialIntelligence, 2012, 25(3): 361-366. (桑妍丽,钱宇华.一种悲观多粒度粗糙集中的粒度约简算法[J].模式识别与人工智能, 2012, 25(3): 361-366)

[12] Meng H L, Ma Y Y, Xu J C. The granularity reduction of pessimistic multi-granulation rough set based on the information quantity[J].JournalofNanjingUniversity(NaturalSciences), 2015, 51(2): 343-348. (孟慧丽,马媛媛,徐久成.基于信息量的悲观多粒度粗糙集粒度约简[J].南京大学学报(自然科学版), 2015,51(2):343-348)

[13] Qian Y H, Li S Y, Liang J Y, et al. Pessimistic rough set based decisions: a multi-granulation fusion strategy[J].InformationSciences, 2014, 264(6): 196-210.

[14] Zhang M, Tang Z M, Xu W Y, et al. Variable multi-granulation rough set model[J].PatternRecognitionandArtificialIntelligence, 2012, 25(4): 709-720.(张明,唐振民,徐维艳,等.可变多粒度粗糙集模型[J].模式识别与人工智能,2012,25(4):709-720)

[15] Yao Y Y,Lin T Y. Generalization of rough sets using modal logics[J].IntelligentAutomation&SoftComputing, 1996, 2(2): 103-120.

[16] Wu Z Y, Zhong P H, Hu J G. The graded multi-granulation rough set[J].FuzzySystemsandMathematics, 2014, 28(3): 165-172.(吴志远, 钟培华, 胡建根.程度多粒度粗糙集[J].模糊系统与数学, 2014, 28(3): 165-172.)

Granulation reduction of graded multi-granulation rough set based on granulation matrix

WANG Xiao-yan, SHEN Yuan-xia

(SchoolofComputerScience&Technology,AnhuiUniversityofTechnology,Ma’anshan243032,China)

Multi-granularity is an effective data processing method in rough set theory. Granularity reduction is the prerequisite for obtaining the concise rules of the information system. The granulation reduction of graded optimism (pessimism) multi-granulation rough set is researched and the lower approximation definition of graded rough set is improved. The granulation matrix of graded multi-granulation rough set is proposed. Based on the granulation matrix, the lower approximation calculation and necessity of granularity are studied in graded multi-granulation rough set. Then the core granulation definition on graded optimism multi-granulation rough set is given. The granulation reduction of graded optimism (pessimism) multi-granulation rough set is proposed based on granulation matrix. Finally, a numerical example is given to demonstrate the correctness of the proposed method for granularity reduction.

graded multi-granulation rough set; granulation matrix; core granulation; granulation reduction

2016-04-12;

2016-09-19;网络优先出版日期:2016-10-22。

国家青年科学基金(61300059)资助课题

TP 18

A

10.3969/j.issn.1001-506X.2016.12.31

汪小燕(1974-),女,副教授,硕士,主要研究方向为数据挖掘、粗糙集理论。

E-mail: wxyzjx@126.com

申元霞(1979-),女,副教授,博士,主要研究方向为智能计算、数据挖掘。

E-mail: yuanxiashen@163.com

网络优先出版地址:http:∥www.cnki.net/kcms/detail/11.2422.TN.20161022.2349.002.html