基于PSO-SVR近似模型的乘员约束系统稳健性优化*

张海洋，胡帅帅，周大永，高剑武，谷先广2，

（1.浙江吉利汽车研究院有限公司，浙江省汽车安全技术研究重点实验室，杭州 311228；2.太航常青汽车安全系统（苏州）股份有限公司，苏州 215100； 3.合肥工业大学汽车与交通工程学院，合肥 230009）

前言

乘员约束系统作为汽车被动安全领域的主要研究对象之一，包括仪表板、安全气囊、安全带、座椅和转向系统等［1］。当汽车发生碰撞时，由安全带等装置组成的乘员约束系统不但可以有效缓冲乘员所受到的冲击载荷，且能避免乘员与车身发生二次碰撞，从而起到保护乘员安全的作用［2］。因此，乘员约束系统的优化设计具有重要意义。

当前乘员约束系统的优化方法主要是建立近似模型，利用优化算法寻求各系统之间的最优参数匹配。由于约束系统中的参数众多，若对所有参数进行优化将导致近似模型的维度过高，近似模型精度得不到保障。为此，有学者将灵敏度分析的方法应用于优化流程中［3－5］。同时，支持向量回归法在处理小样本、非线性、高维度等问题上比传统近似模型更有优势［6］，但该近似模型中的参数及核函数众多，构建近似模型之前需要通过优化算法对其进行合理优化。另外，为保证产品质量，须在传统的确定性优化基础上进行稳健性优化［1，7－8］。

综上所述，在对乘员约束系统的优化过程中，首先建立某款乘用车正面碰撞乘员约束系统数值模型，并与物理试验数据进行对标，验证模型的有效性。应用全局灵敏度方法筛选优化对象，并采用粒子群优化算法对支持向量回归模型中的参数及核函数参数进行优化，从而建立PSO-SVR近似模型。同时，在确定性优化的基础上进行稳健性优化，得到该约束系统的最优结果。

1 PSO-SVR近似模型

1.1 SVR近似模型

支持向量回归机是支持向量机（support vector machine，SVM）在函数拟合领域的应用。针对训练样本｛（x1，y1），（x2，y2），…，（xn，yn）｝，SVR的研究目的是利用某一函数表示x和y之间的关系，即给定某一x值，该函数能够得到相应的预测值y。支持向量回归模型的形式为［9］

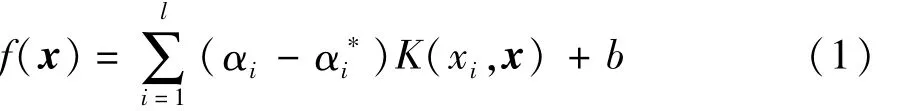
式中：l为样本点的个数；αi和αi*为针对不同约束条件的拉格朗日乘子；K（xi，x）为核函数；b为真实值与预测值的偏差量。根据结构风险最小化法则，求解函数f（x）可转化为优化求解问题：

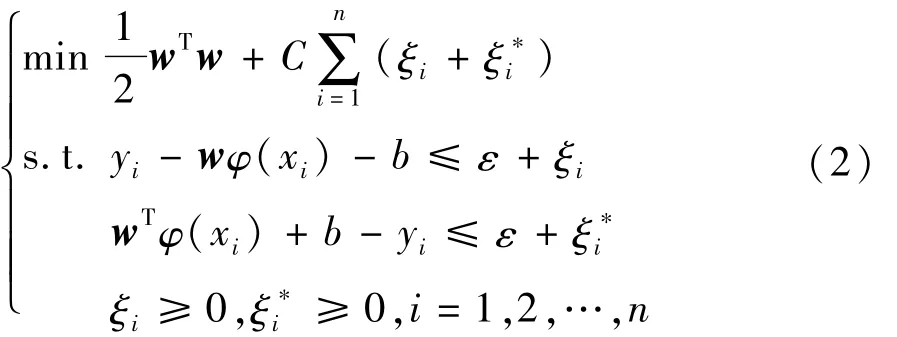
式中：w为权重向量；ξi和为松弛因子；ε为不敏感系数；C为惩罚系数且C＞0，它控制对超出误差ε的样本的惩罚程度，合适的C值能使模型具有较好的推广能力。

多种核函数可以应用在SVR模型中，使用不同核函数构建的近似模型预测精度有很大差异，典型的核函数如表1所示。

对于线性问题，通常使用线性型核函数；对于非线性问题，考虑使用高斯型或多项式型核函数。核函数分全局核函数和局部核函数，为提高SVR近似模型的适用范围，采用式（3）所示的混合核函数处理非线性问题。

表1 典型核函数

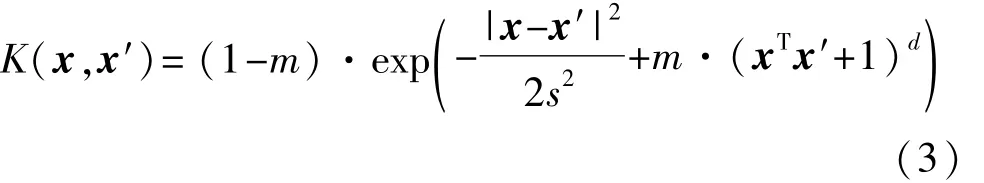
1.2 PSO-SVR近似模型

为提高近似模型的预测精度，采用粒子群算法对SVR近似模型的参数进行优化。待优化的参数有惩罚系数C、不敏感系数ε和核函数参数m、s、d。近似模型的精度可由确定性系数R2和均方根误差Er来评价，其表达式为［8］

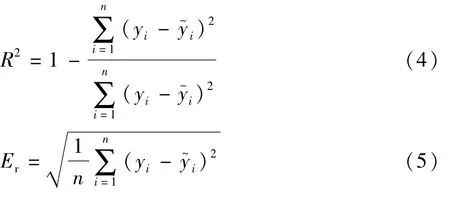
PSO-SVR近似模型的具体建立过程如下：（1）确定优化变量、优化目标和约束，本文中优化变量为表2中的参数，目标和约束分别为R2和Er；（2）通过试验设计（design of experiments，DOE）得到样本点和验证点的数据；（3）应用PSO算法进行优化迭代；（4）获得SVR模型参数的优化值并进行统计；（5）针对不同响应，依次进行上述步骤（1）－（4）。

2 乘员约束系统模型的建立与验证

2.1 约束系统模型的建立

首先建立了吉利某车型正面100%重叠刚性壁障碰撞的驾驶员侧乘员约束系统模型，如图1所示。具体步骤如下：（1）根据试验车实际参数建立驾驶室模型，包括转向系统、仪表板、防火墙、踏板系统、地板和座椅系统等；（2）导入50百分位的混Ⅲ男性假人模型并调整其坐姿；（3）配置安全带和安全气囊；（4）定义接触关系；（5）定义模型输入，包括Z向的重力场和X向的加速度场，其中后者是试验车根据C-NCAP中正面100%重叠刚性壁障碰撞工况下B柱下端传感器测得的减速度曲线。

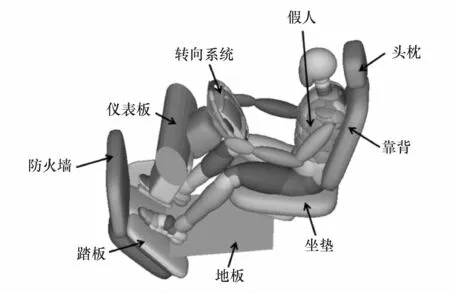
图1 乘员约束系统模型

2.2 约束系统模型验证

约束系统仿真模型的精确度是后续优化问题的基础，在优化之前需要先进行模型验证。首先，表2给出了典型伤害指标的仿真与试验结果对比，各项误差均小于10%。其次，图2给出了仿真模型与实车试验在不同时刻下假人的姿态对比，可以看出，仿真与试验结果基本一致。因此，本文中建立的仿真模型满足精度要求。

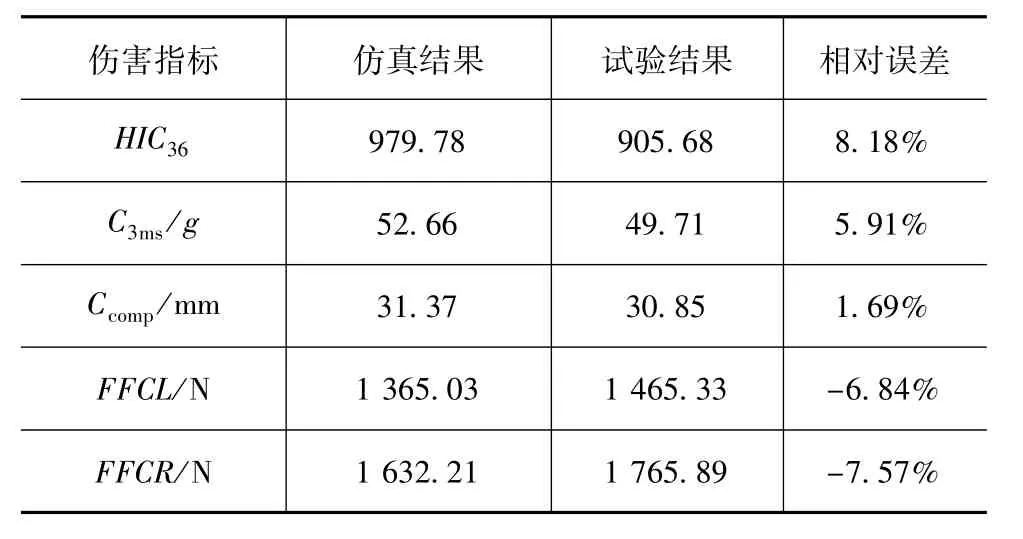
表2 伤害指标仿真与试验结果对比

3 乘员约束系统稳健性优化

3.1 优化问题定义

3.1.1 设计变量的选择

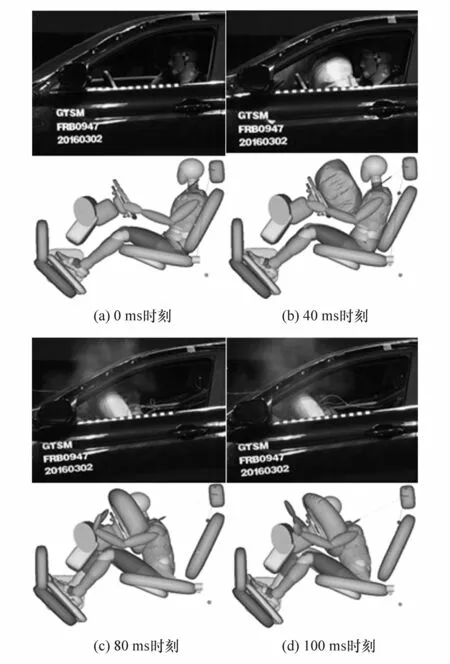
图2 不同时刻仿真与试验乘员姿态对比

主要对直接保护乘员的安全带和安全气囊进行优化，从两者中预选9个设计参数，其中安全带设计参数包括限力等级、预紧时间、织带刚度等级和织带伸长量；安全气囊设计参数包括排气孔直径、拉带长度、起爆时间、充气质量流率比例和气囊体积。在灵敏度分析中，为综合反映各参数对乘员各部位伤害值的影响，选择加权伤害准则WIC作为评价标准，其表达式［10］为

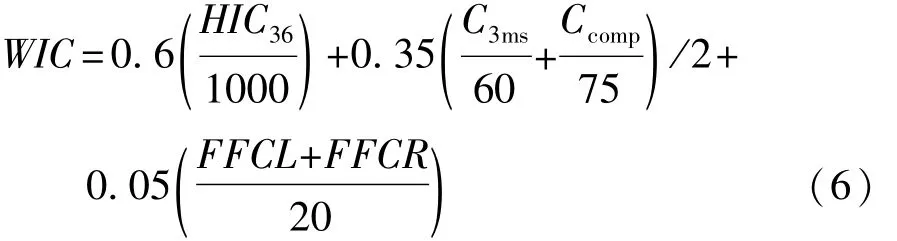
应用 Sobol法计算全局灵敏度［3－5］，结果如图 3所示。根据全局灵敏度，选择安全带限力器限力等级x1及预紧器预紧时间x2、气囊排气孔直径x3、充气质量流率比例x4及气囊体积x5，作为后续乘员约束系统优化的设计变量。根据生产厂家的实际情况确定设计变量的取值范围与分布，如表3所示。

3.1.2 优化目标和约束条件

以兼顾头、胸、腿部的加权伤害指标WIC作为优化目标，以头部伤害指标HIC36、胸部伤害指标Ccomp与C3ms和左右大腿轴向力FFCL与FFCR作为约束条件进行优化。参考乘员保护国家标准GB 11551及C—NCAP中的评价标准，确定各约束条件的目标值，连同初始值，列于表4。

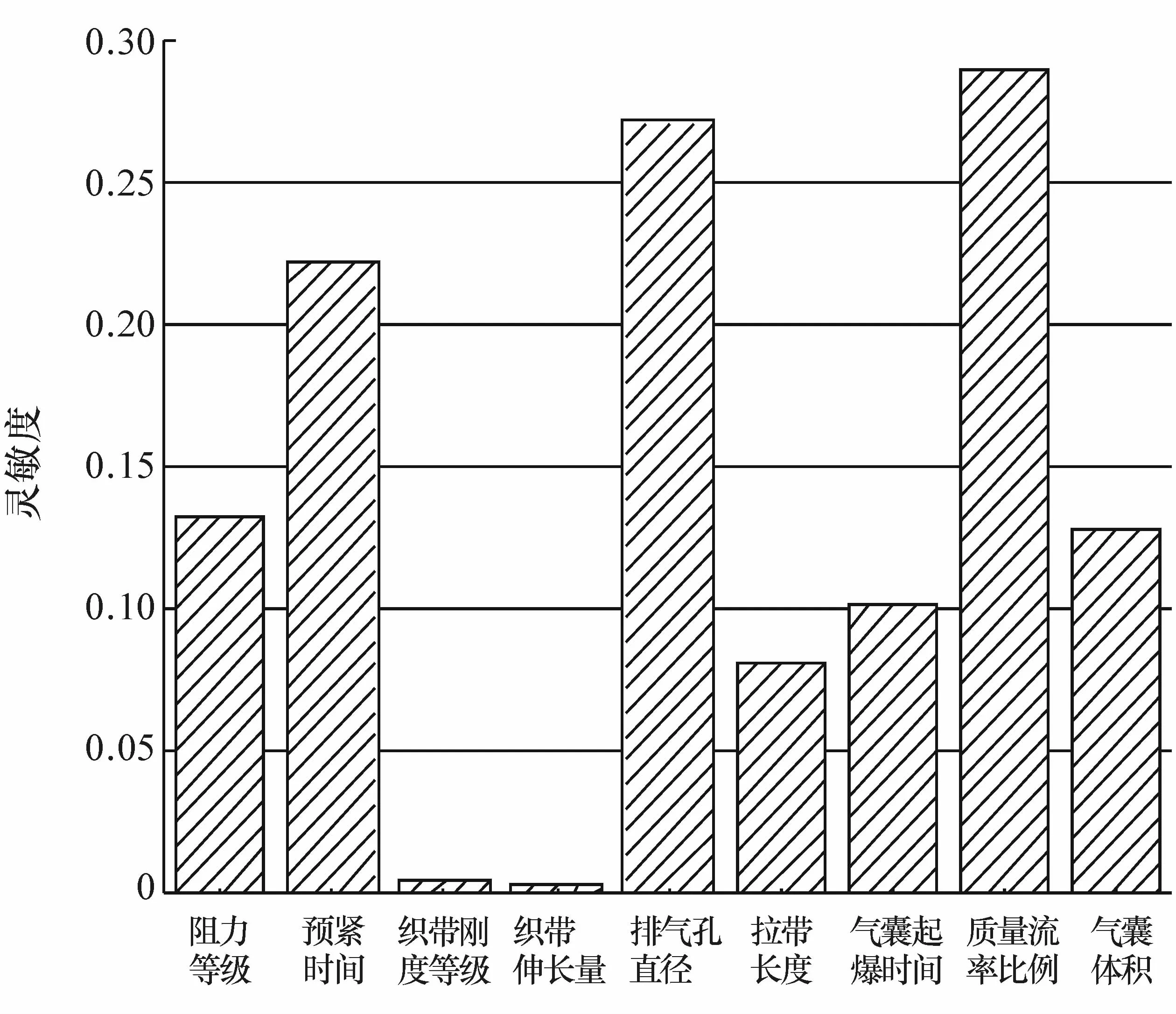
图3 WIC对各设计参数灵敏度的对比

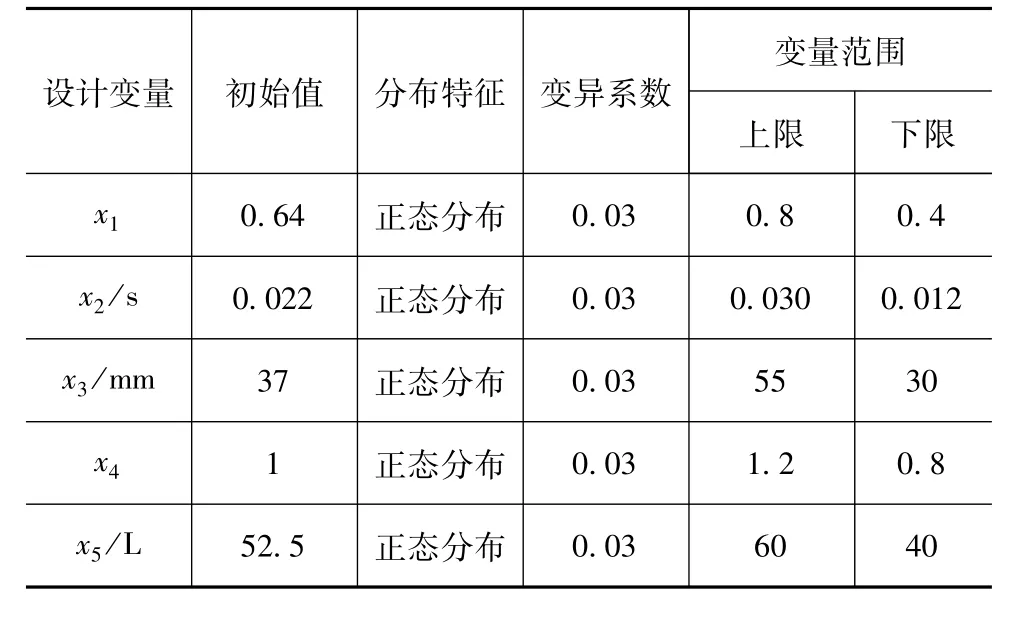
表3 设计变量的取值范围和分布情况

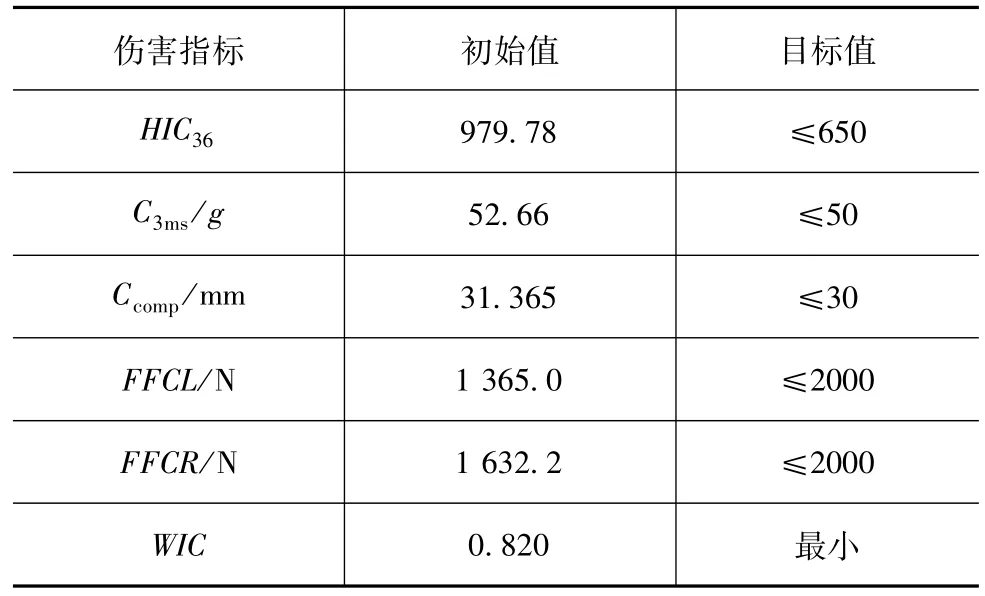
表4 伤害指标初始值和优化的目标值

3.2 试验设计

通过试验设计可以合理、高效地获得数据信息。本文中使用填充性能优良的最优拉丁超立方（optimal Latin hypercube，OLH）试验设计方法获得样本点数据。在设计空间中应用两次OLH试验设计方法分别抽取120组样本点数据和30组验证点数据。按照DOE数据修改仿真模型参数并提交计算，统计并计算各伤害指标值。

3.3 PSO-SVR近似模型的建立

根据DOE数据计算相应的响应值，构造近似模型。应用PSO算法对SVR模型中的参数进行优化，结果如表5所示。同时构建传统的克里金（Kriging，KRG）、响应面（response surface model，RSM）和径向基函数（radial basis function，RBF）近似模型，比较三者与优化后的SVR模型的精度，对比结果如表6所示，PSO-SVR近似模型拥有更高的精度，可以用于后续优化。

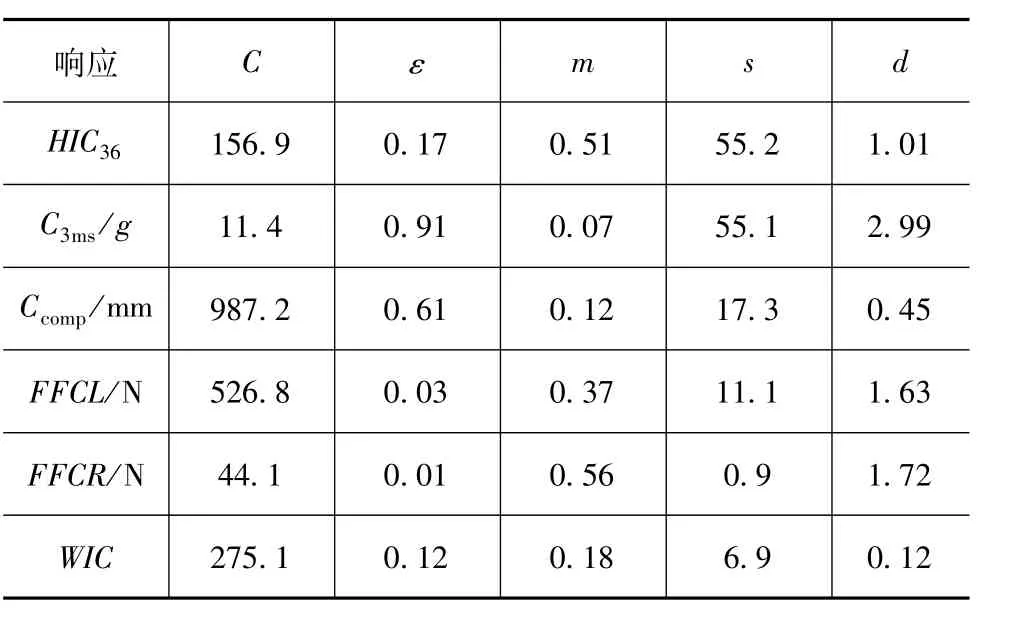
表5 SVR模型参数优化结果

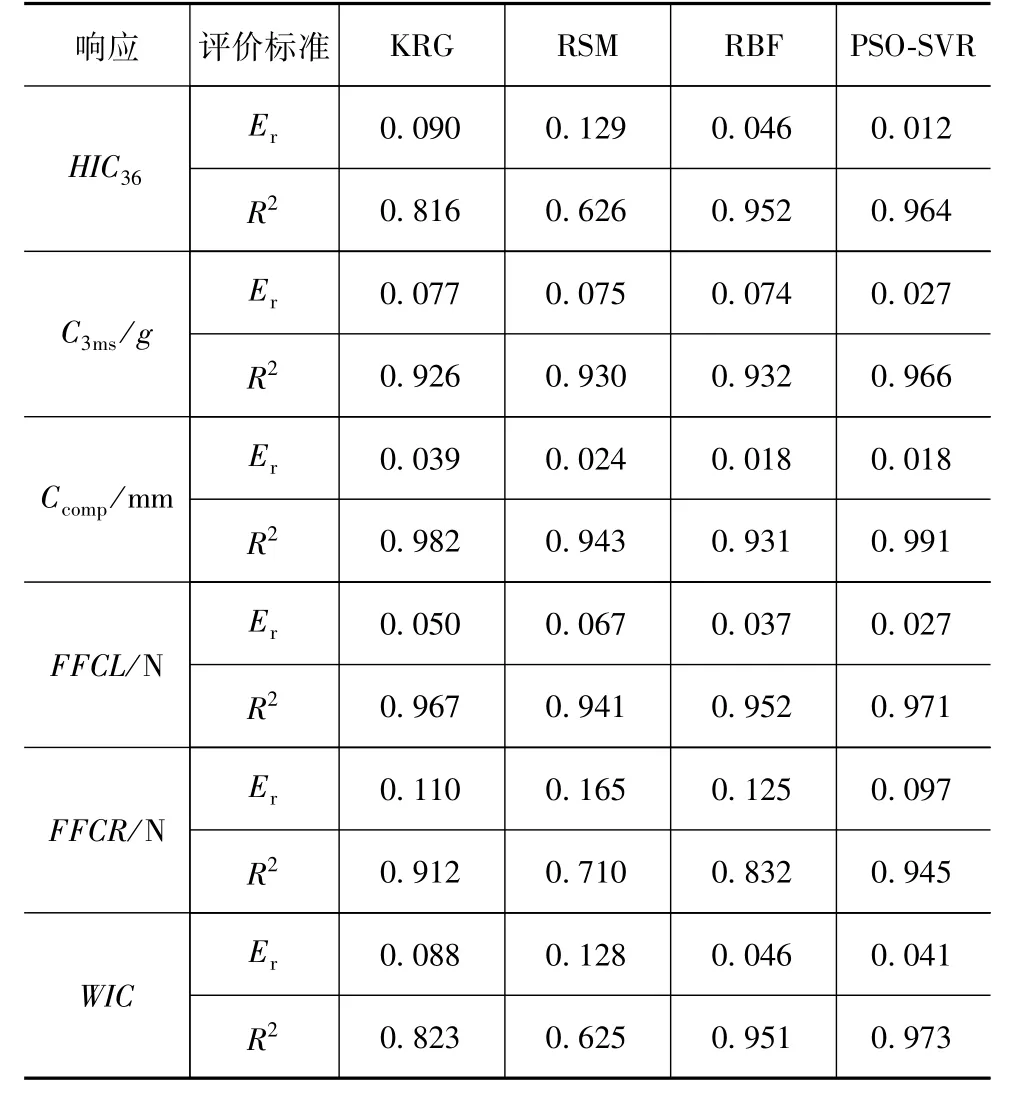
表6 不同近似模型精度对比

3.4 优化过程与结果分析

3.4.1 确定性优化

该问题的确定性优化数学表达式为

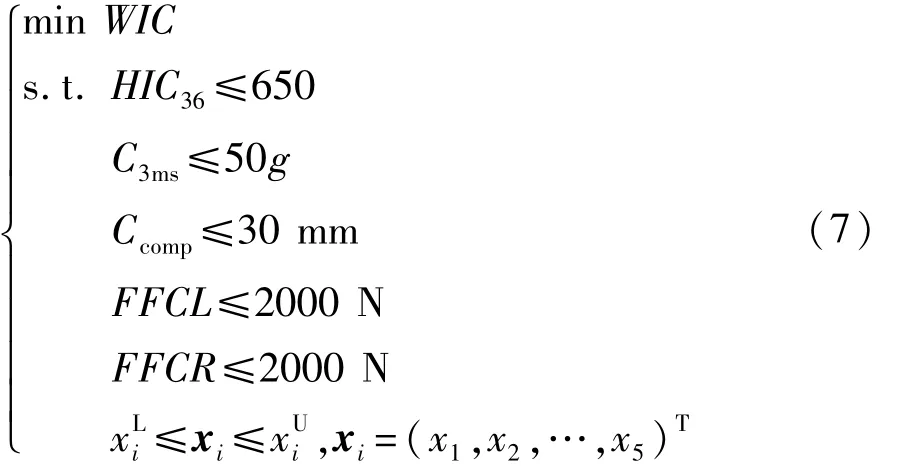
采用多岛遗传算法（multi-island genetic algorithm，MIGA）调用建立的PSO-SVR近似模型进行优化，结果如表7所示，设计变量优化结果见表8。可以看出，仿真值与预测值相对误差最大为1.6%，因此PSO-SVR近似模型的可信度较高。

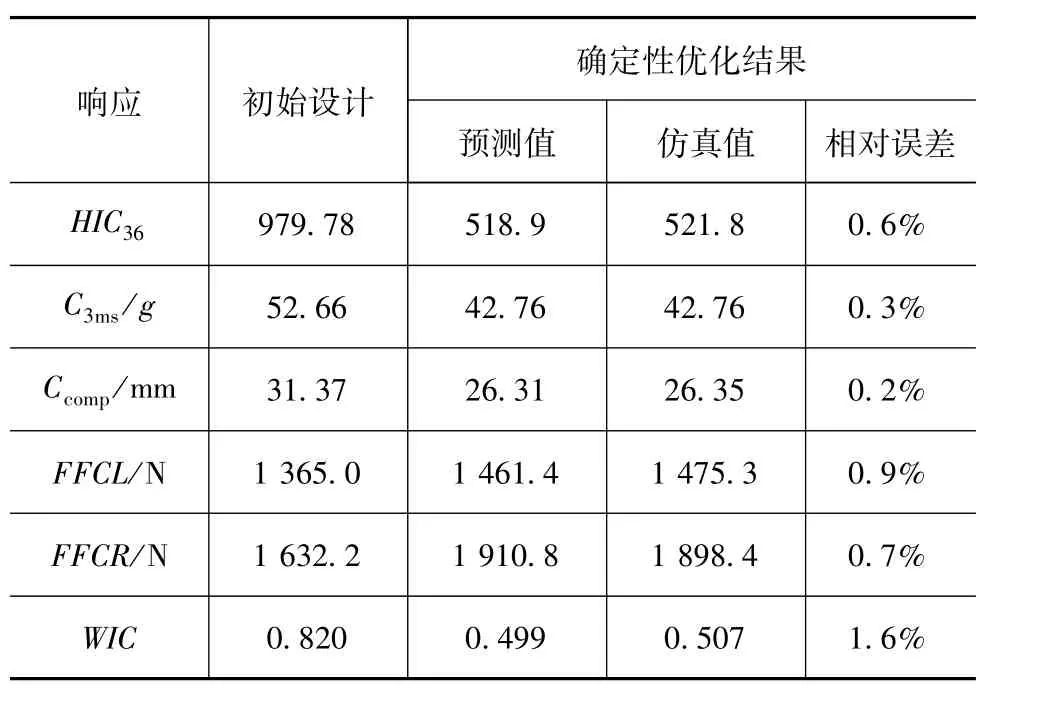
表7 确定性优化结果

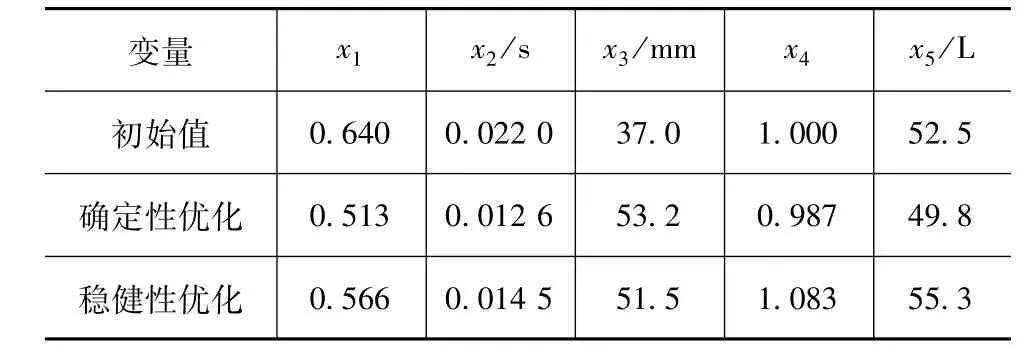
表8 设计变量优化结果

为控制约束函数响应的波动，降低优化解的敏感性，对确定性设计进行了可靠度评估。根据表3中设计变量的分布，对设计变量采用蒙特卡罗描述性抽样方法抽取2 000组数据，并调用PSO-SVR近似模型进行计算，各响应的均方差和可靠度如表9所示。工程上要求产品的可靠度需要达到99%以上，确定性优化解中头部及胸部伤害指标的可靠度均不满足要求，在实际应用中存在设计失效的风险，需要对其进行稳健性优化。

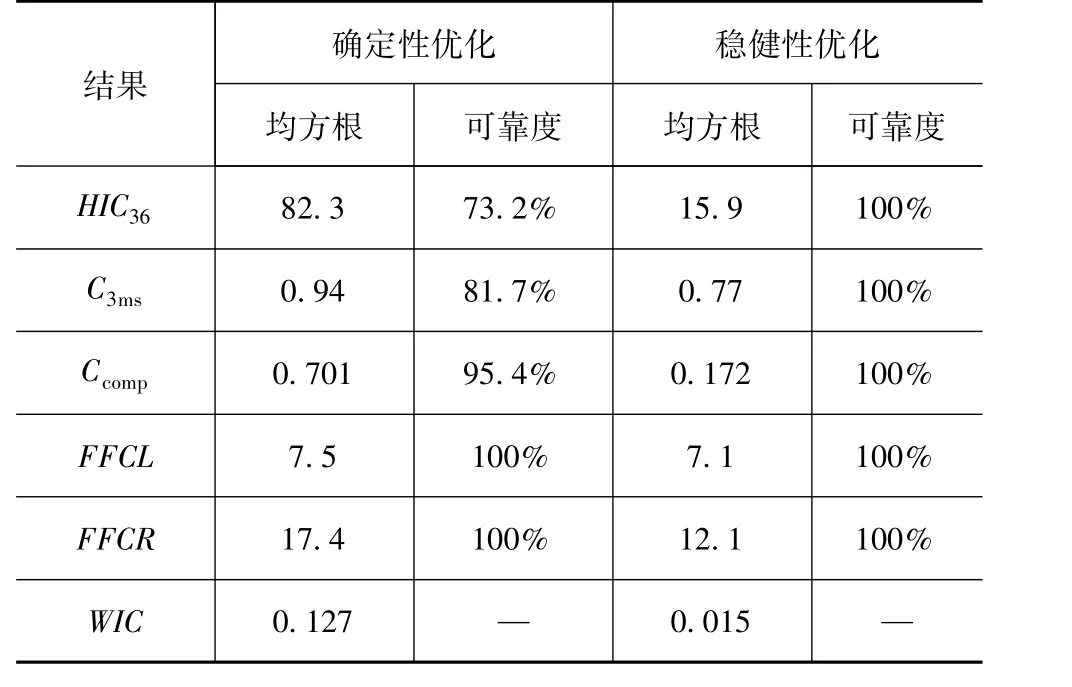
表9 稳健评估结果

3.4.2 稳健性优化设计

稳健性优化考虑了设计变量波动对优化结果的影响，其数学表达式为

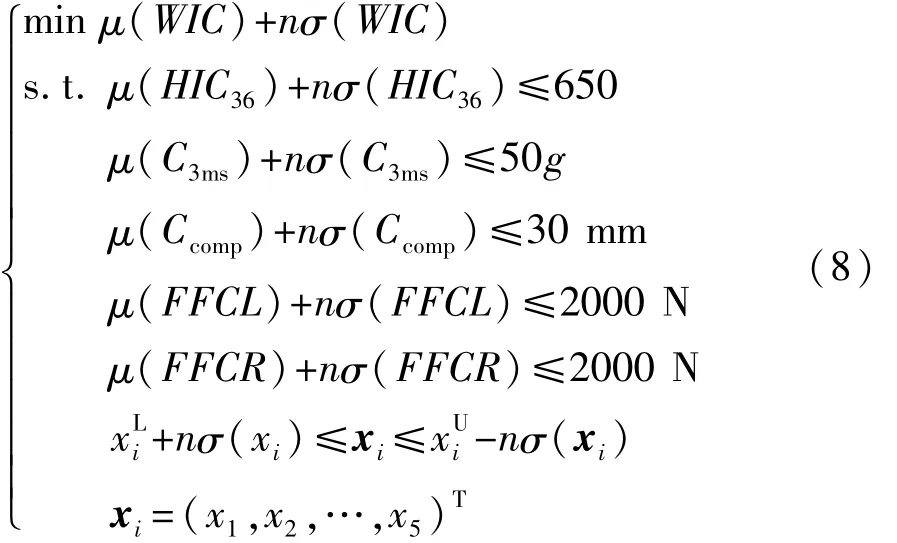
式中：μ和σ为各响应参数的均值和均方差；n为稳健性优化中的σ水平，其水平越高，优化过程中对响应的稳健性要求也越高，本文中n的取值为6。用蒙特卡罗描述性采样方法［11］，将采集的样本点代入PSO-SVR近似模型中进行稳健性优化。

对稳健性优化的结果进行稳健性评估，同列于表9中。各约束响应的可靠度均为100%，且均方根均得到明显降低，满足工程应用要求。

3.5 优化结果的仿真验证

优化过程中使用近似模型代替仿真模型，因此需要将优化结果进行仿真验证。稳健性优化最终得到的设计变量取值如表8所示。优化值与仿真值对比如表10所示。从仿真结果分析，虽然约束响应FFCL和FFCR有所增加，但均在可接受的范围内；目标响应WIC降低了31.7%，优化效果明显。同时，预测值与仿真值的最大误差为2.0%，表明构造的PSO-SVR近似模型具有较高的预测精度。

图4给出了初始设计、确定性优化与稳健性设计优化结果的头部X向加速度曲线和胸部压缩量曲线。虽然确定性优化的结果要优于稳健性优化，但考虑到确定性优化后的可靠度不满足要求，因此选择稳健性优化为最终优化结果。

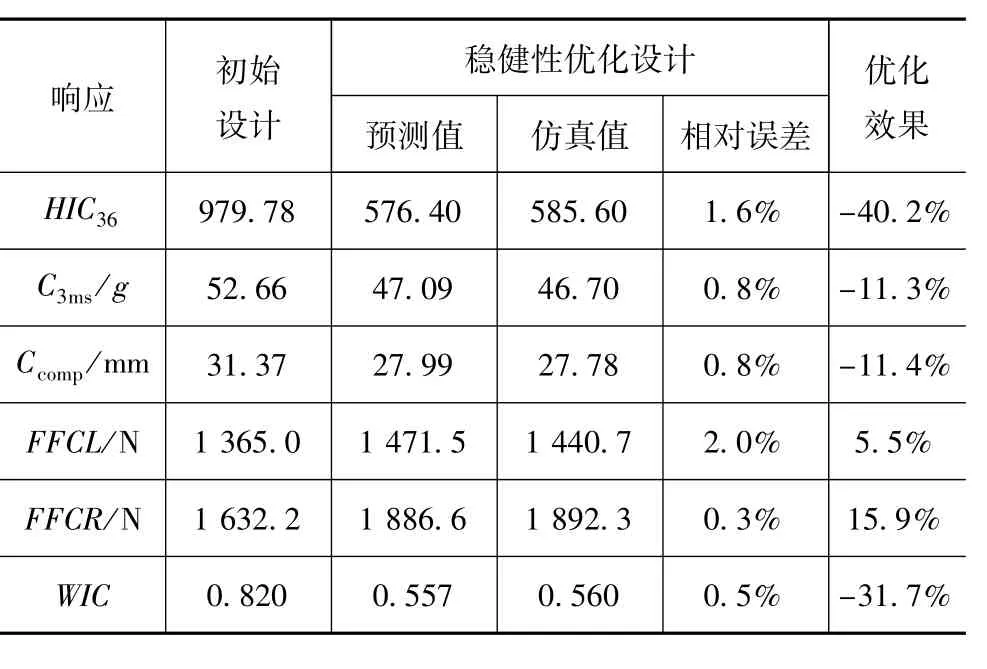
表10 稳健性优化结果

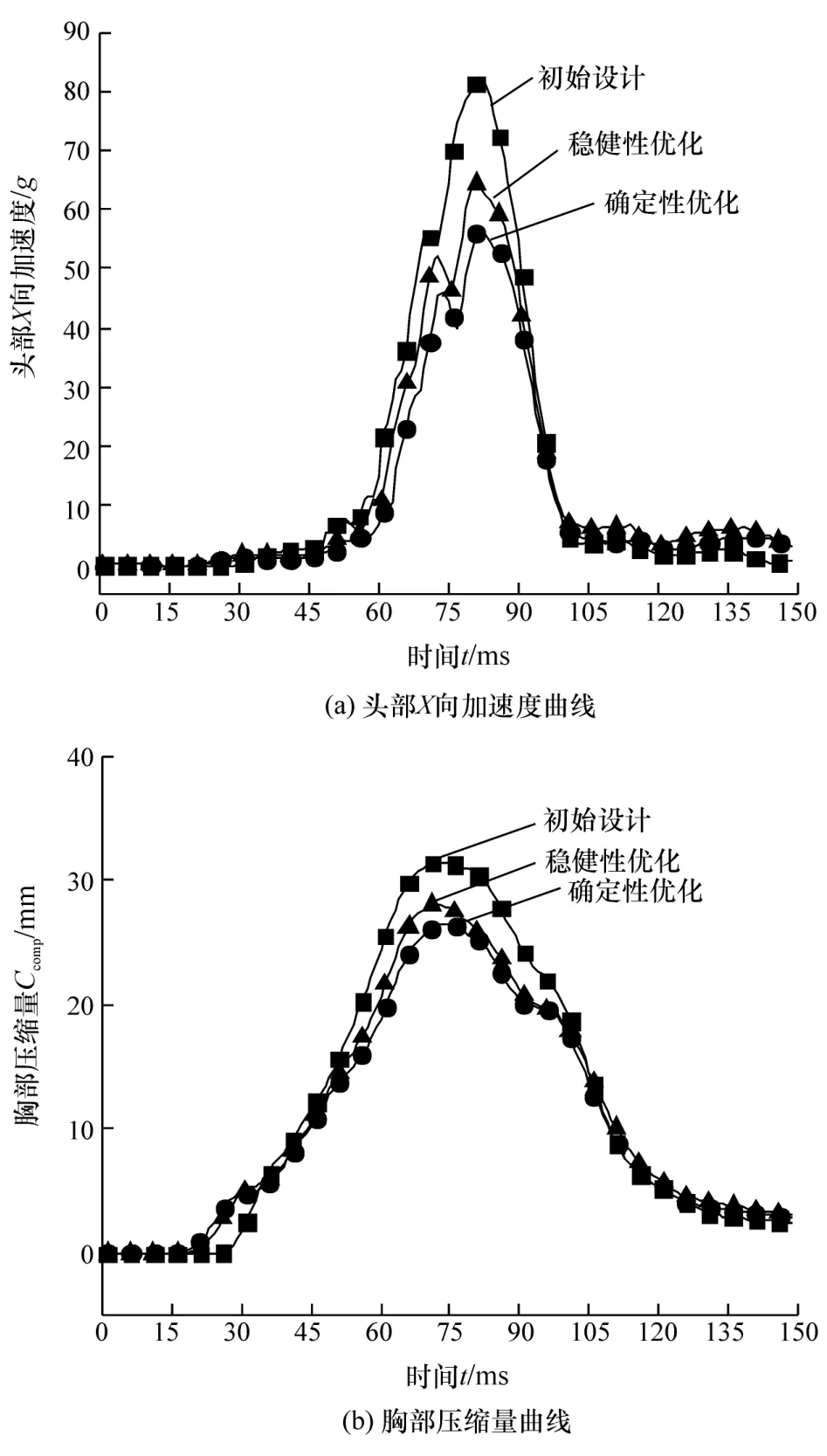
图4 优化结果曲线对比

4 结论

（1）通过粒子群算法对支持向量回归模型中的参数和加权核函数的参数进行优化，构建了比传统近似模型精度更高的PSO-SVR模型，并应用于后续优化过程中。

（2）确定性优化得到满足损伤指标要求的优化解，但它们不满足可靠度要求，设计变量的波动可能会导致产品性能的降低甚至是失效。

（3）通过稳健性优化可以得到既满足设计要求又兼顾稳健性的优化结果。通过本文的优化，加权伤害准则降低了31.7%。