不同温度与荷电状态下锂离子电池传荷电阻估计*

李日康，王学远，2，戴海峰，魏学哲

（1.同济大学，新能源汽车工程中心，上海 201804； 2.同济大学电子与信息工程学院，上海 201804）

前言

锂离子电池在电动汽车中广泛应用。但是，随着比能量提升，电池寿命问题成为其安全、高效车载应用和梯次利用的关键技术问题。电池老化过程中伴随容量衰减和阻抗上升［1］，因此可基于阻抗来表征电池寿命。

锂离子电池交流阻抗谱反映锂离子在电极界面和固液相的扩散传导特性，阻抗成为研究电池内部特性的常用工具。随着可靠的车载电池阻抗测量方案提出［2］，使得车载条件下利用阻抗进行电池老化状态估计成为可能。电池工作过程包括多种电化学反应和物理过程，电池老化会伴随电化学反应阻抗增加，体现在电化学阻抗谱（electrochemical impedance spectroscopy，EIS）中低频区域的传荷电阻，代表电极界面反应进行的难易，其受电池荷电状态（state of charge，SOC）、温度和老化状态影响。电池老化过程中电池传荷电阻相比于欧姆内阻表现出更加明显的上升趋势［3］，可通过传荷电阻来表征电池寿命变化［4］。但是，已有研究在利用传荷电阻表征电池寿命时并没有考虑荷电状态与温度的影响，使得基于传荷电阻的寿命估计和预测方法的适用性受到影响。

为此，本文中第1章从电池电化学机理模型出发，考虑电池副反应进行老化建模，分析老化过程中正负极上传荷电阻变化；然后从电极界面反应机理出发推导传荷电阻近似表达式，提出在不同温度和荷电状态下传荷电阻的折算方法；最后通过获取4节不同老化工况下的电池单体在不同状态下的传荷电阻，对传荷电阻折算方法的有效性进行了验证。

1 锂离子电池伪二维模型

Doley等人对锂离子电池内部电化学反应进行研究，提出了锂离子电池伪二维模型（pseudo-two-dimensions，P2D）［5］，如图 1所示。

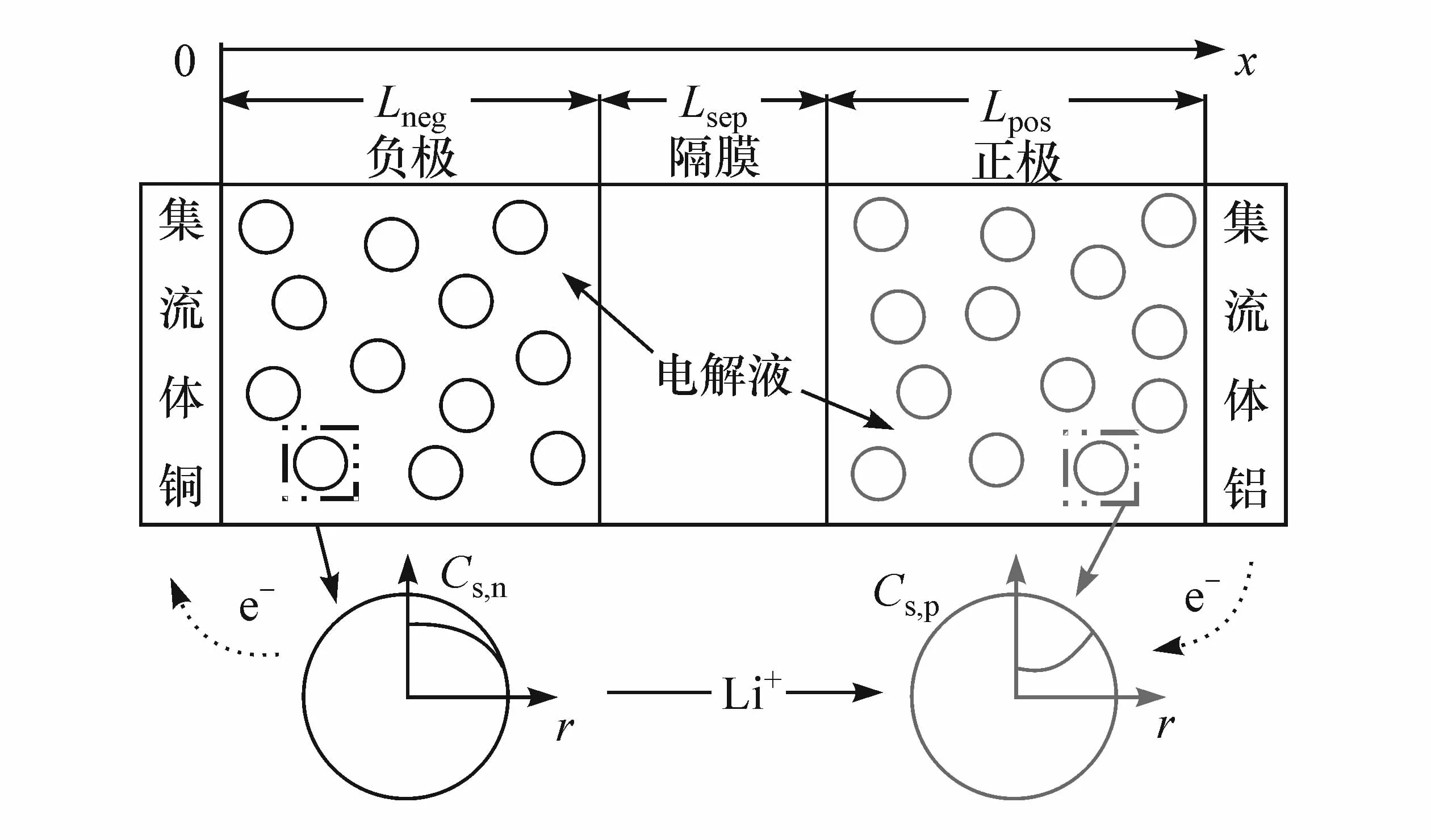
图1 锂离子电池伪二维模型示意图

1.1 锂离子固相扩散

正负极区域锂离子固相扩散满足Fick扩散第二定律：

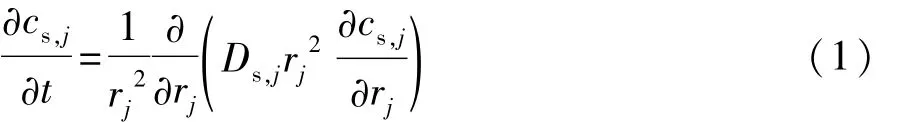
式中：cs为固相锂离子浓度；Ds为固相锂离子扩散系数；在电池负极、隔膜以及正极区域，下标分别对应为 j＝neg，sep，pos。

电池正负极满足以下边界条件：

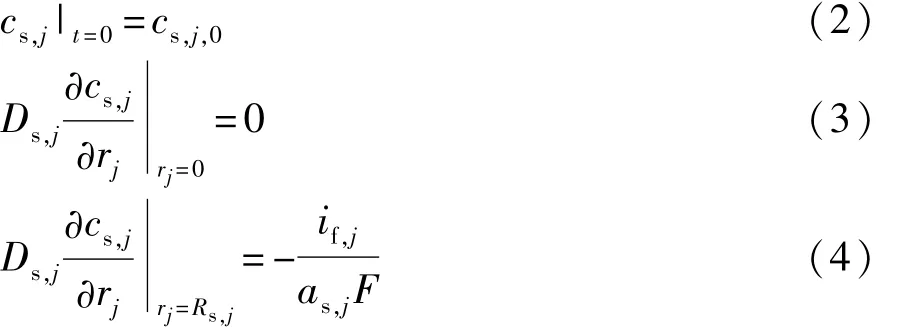
式中：Rs为电极球形颗粒半径；if为局部电流密度；F为法拉第常数；as为比表面积。

式中εs为电极固相体积分数。

1.2 锂离子液相扩散

正负极区域液相扩散满足方程：

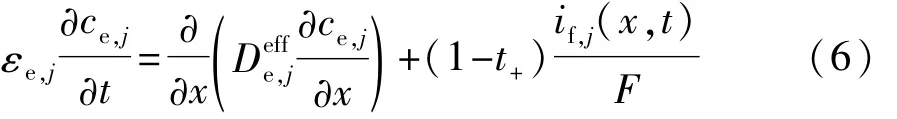
隔膜区域液相扩散满足方程：

式中：ce为液相锂离子浓度；εe为液相体积分数；t＋为液相中锂离子迁移数为锂离子有效液相扩散系数。

式中：De为液相扩散系数；Brugg系数描述多孔电极导致的锂离子在电解液中曲折迁移。

电池内部液相扩散过程满足边界条件：

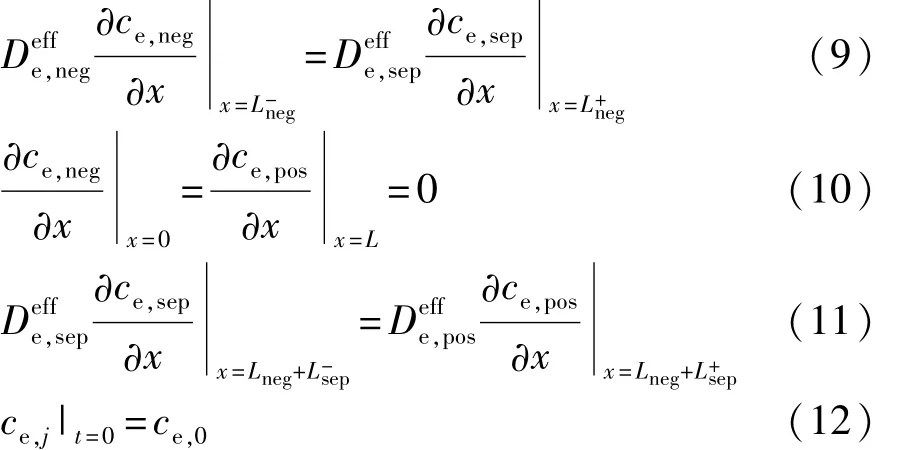
式中：0≤x≤L；Lneg为负极厚度；Lsep为隔膜厚度；Lpos为正极厚度；L为正负电极与隔膜厚度总和。

1.3 固相电势分布

正负极固相电势φs分布符合欧姆定律：

满足以下边界条件：

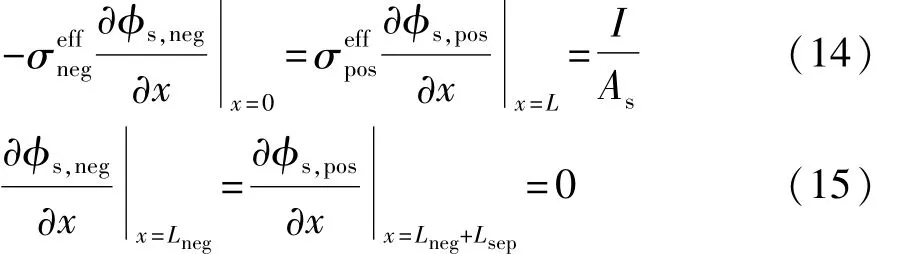
式中：I为电池电流；As为电极表面积；σeff为固相有效离子电导率。

σ为固相材料电导率，则σeff满足等式：

1.4 液相电势分布

电池液相电势φe分布满足欧姆定律：

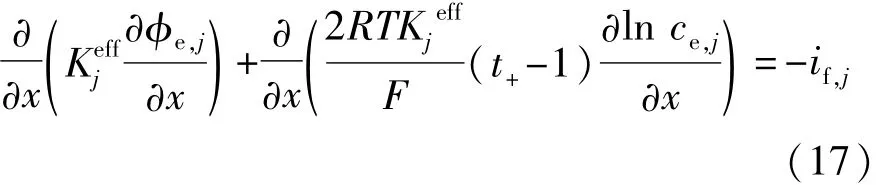
且满足以下边界条件：

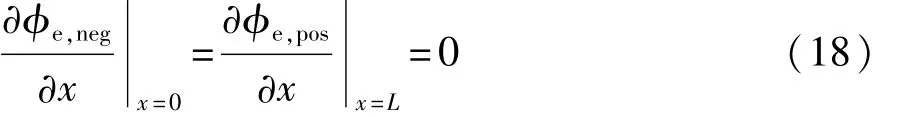
式中：R为通用气体常数；T为电池温度；Keff为电解液的有效离子电导率。

K为电解液离子电导率，则有

电解液离子电导率满足关系式［5］：

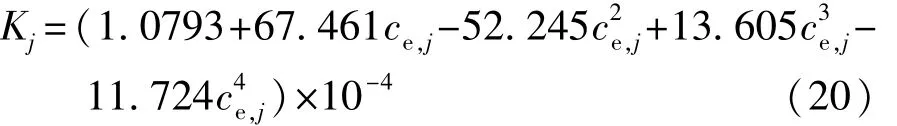
式中 0＜ce，j＜2.5 mol／dm3。

1.5 电极动力学

使用Butler-Volmer方程来描述电池正负极固液相界面的动力学：

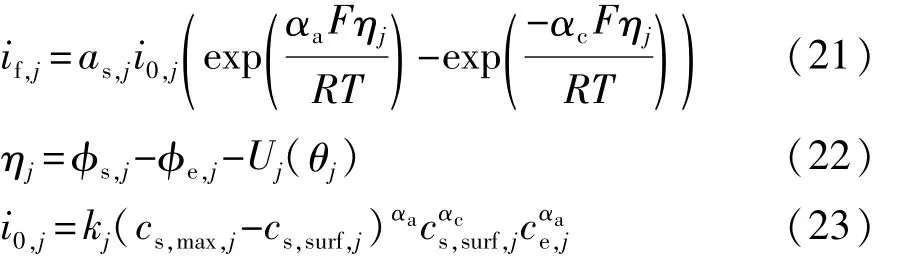
式中：i0为交换电流密度；η为电极过电位；αa与αc为传递系数；U为电极平衡电势；θ为电极SOC；k为反应速率常数；cs，max为固相最大锂离子浓度；cs，surf为表面锂离子浓度。

1.6 电池老化副反应建模

电池内部副反应是电池老化的重要原因，通常认为电池老化是由充放电过程中活性锂离子损失、活性材料损失、电解液干涸、负极结构坍塌等副反应造成［1］。本文中将电池老化过程中活性锂离子损失和正极活性材料损失与P2D模型结合，分析老化过程中传荷电阻变化。

1.6.1 活性锂离子损失

活性锂离子损失主要由负极固体电解质膜（solid electrolyte interphase，SEI）形成导致，SEI膜在首次充电过程中形成并消耗锂离子，造成电池容量不可逆损失［6－7］。Ramadass等人认为在充电过程中负极上锂离子与溶剂反应形成SEI膜，导致溶剂减少与锂离子不可逆损失［8］。负极产生的膜阻Rfilm满足下式：

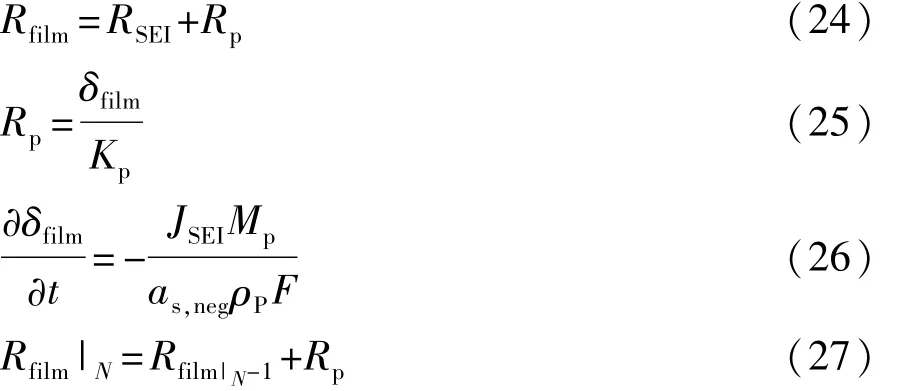
式中：RSEI为膜阻初值；Rp为副反应增加膜阻；N为电池循环次数；δfilm为膜厚；Kp为膜电导率；ρP为密度；Mp为摩尔质量；JSEI为SEI膜局部电流密度。JSEI满足如下等式［6］：

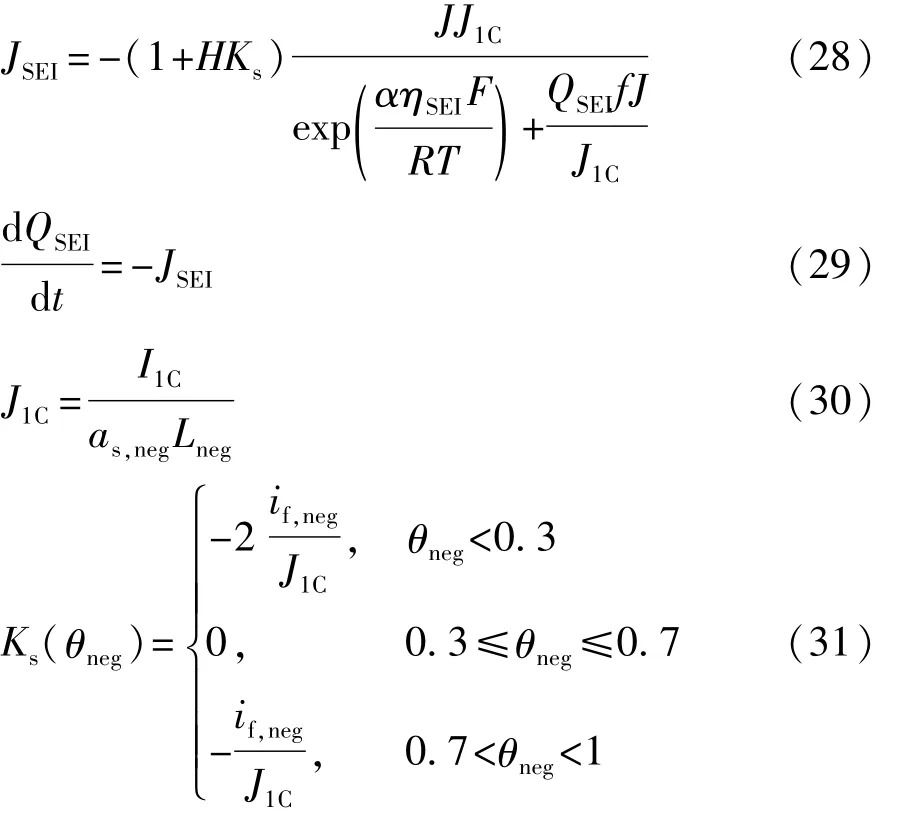
式中：ηSEI为副反应过电位；QSEI为负极副反应消耗锂离子而损失的容量；J1C为电池1C倍率放电时负极电流密度；α为副反应过程传递系数；f、J、Ks、H为集总参数。副反应表达式（24）～式（31）发生在电池充电过程中。

负极局部电流密度与副反应过电位满足式（32）［8］，仿真参数如表 1所示。

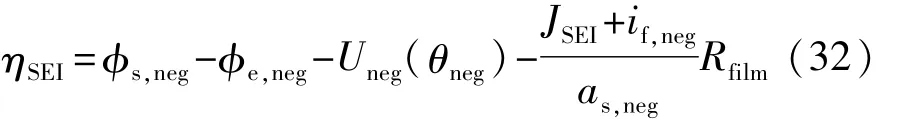
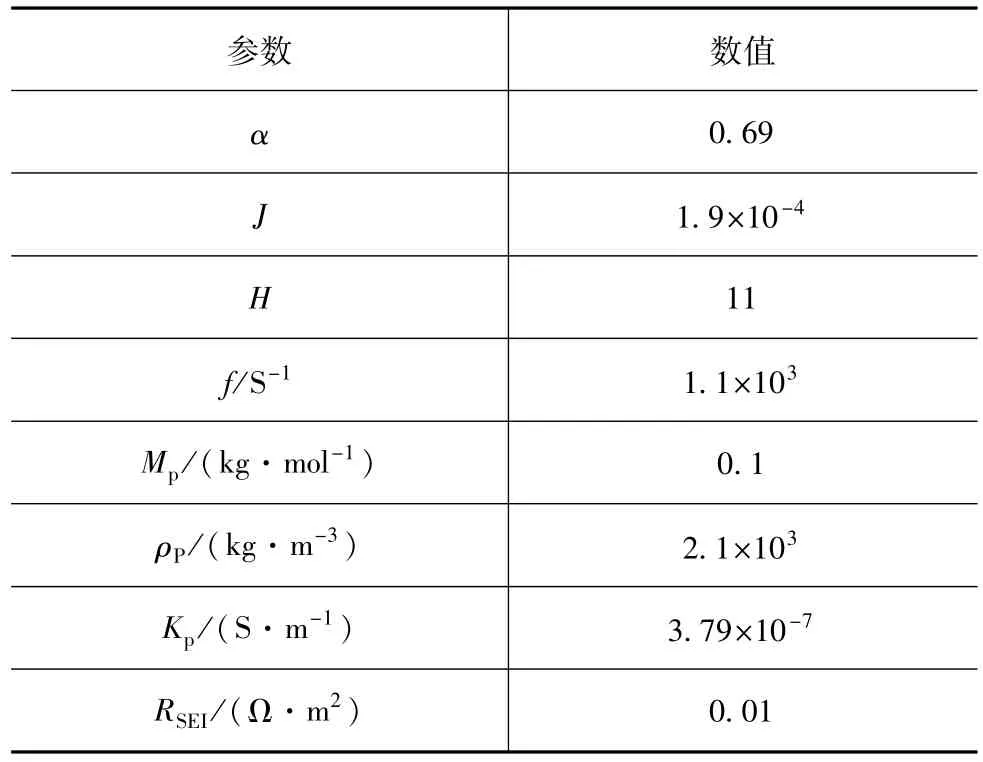
表 1 负极副反应仿真参数［6，8－9］

1.6.2 正极活性材料损失

Zhang等人分析LiNiCoO2电池老化过程中容量衰退的不同阶段，发现电池容量衰退过程中，负极材料体积分数基本不变，而正极材料体积分数逐渐减小，在电池老化后期容量衰退主要由正极活性材料损失引起［10］。Kindermann等人针对NCM电池构建正极体积分数下降模型分析电池老化［11］。Dai等人研究LiMn2O4正极材料容量衰退过程，认为正极在老化过程中活性材料体积分数减小部分等于副反应引起的非活性材料体积分数增加部分［12］。以上学者对不同类型锂离子电池的研究均认为老化过程中正极活性材料体积分数逐渐下降。本文中选取Zhang等人提出的正极老化模型，体积分数变化符合下式［10］：

式中A、B、C为拟合经验参数。

1.7 电池模型仿真

选用正极材料为镍钴铝、标称容量为2.75 A·h的三星INR18650－29E锂离子电池进行循环老化。老化工况为：先恒流恒压充电，充电电流为 1C（2.75 A），截止电压为4.2 V，截止电流为1／20C，然后恒流放电，放电电流为1C，放电截止电压为2.5 V，置于25℃恒温箱循环150次。同时对利用COMSOL5.3a软件构建的电池老化模型进行相同老化工况仿真，包含P2D模型、负极SEI膜增长模型与正极活性材料损失经验模型。仿真参数主要来源于文献和软件材料库，如表2所示。

1.8 模型仿真结果

通过实验获取电池在25℃下每循环老化50次的1C倍率放电曲线，并与COMSOL中电池老化模型仿真结果作对比。如图2所示，模型仿真与实验放电曲线相近，所建立模型能较好地反映电池老化过程中放电过程。

1.9 电池老化过程中正负极传荷电阻变化

由 Butler-Volmer方程得传荷电阻 Rct［14］：

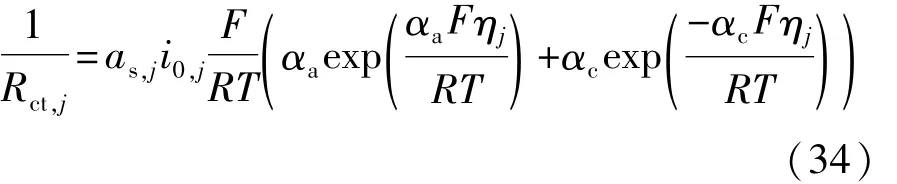
当αa＝αc＝0.5时，传荷电阻表达式简化为

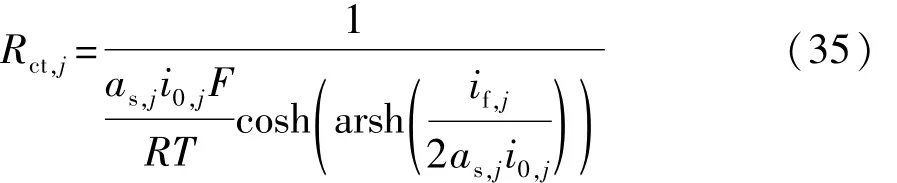
由式（35）绘制电池放电过程和老化过程中正负极上传荷电阻变化，如图3和图4所示。

从图3可知放电过程中正极传荷电阻大于负极。图4表明电池电压为4.2和2.5 V时，电池老化过程中正极传荷电阻逐渐增加，而负极传荷电阻相比于正极基本不变。传荷电阻决定电池中低频阻抗，而电池中低频阻抗主要是由正极决定［15］。因此，综上考虑可使用正极传荷电阻来近似代替电池传荷电阻。

表 2 电池仿真参数［8，13］

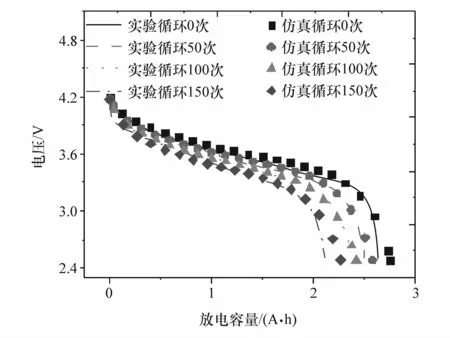
图2 电池不同循环次数下1C倍率放电曲线对比

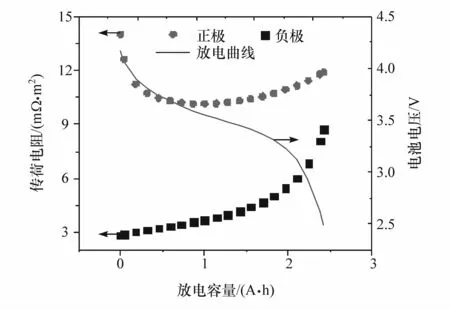
图3 循环100次放电过程中正负极传荷电阻的变化

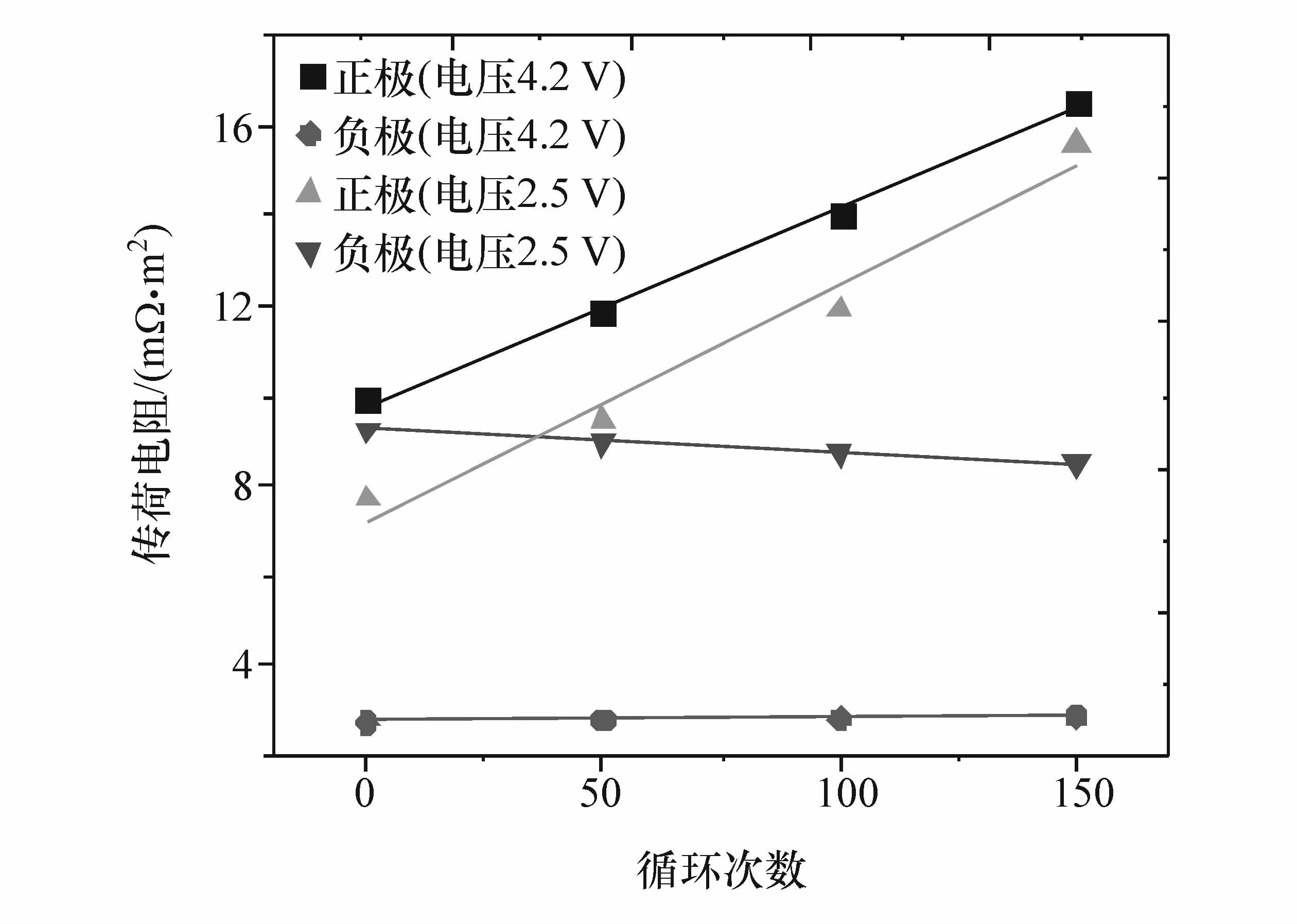
图4 电池电压为2.5和4.2 V时老化过程中正负极上传荷电阻的变化

2 传荷电阻与荷电状态、温度关系

温度和荷电状态对电池内阻有重要影响，须建立传荷电阻与温度、荷电状态的关系式。对Butler-Volmer方程进行1阶泰勒展开［14］：

则可以得到正极传荷电阻的表达式为

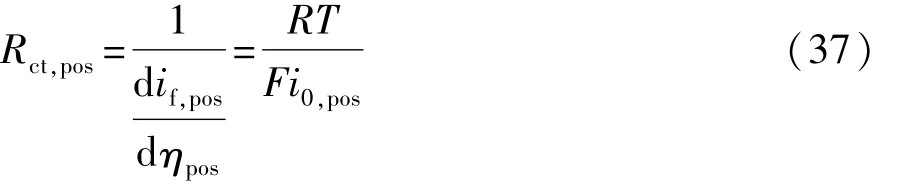
将式（23）正极i0表达式代入式（37）可得

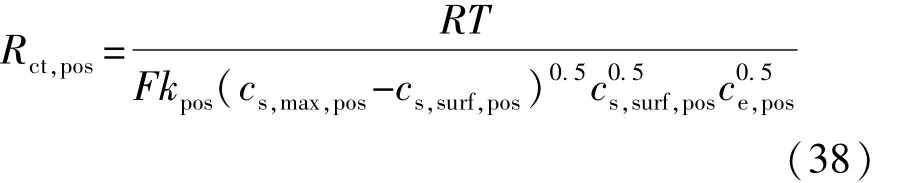
正极 θpos与电池 SOC存在关系［14］：

式中：θ100%，pos为电池充满电时正极荷电状态；θ0%，pos为电池放空时正极荷电状态；Cs，avg，pos为正极颗粒平均锂离子浓度。近似认为 Cs，avg，pos≈ Cs，surf，pos，由式（38）～式（40）可得

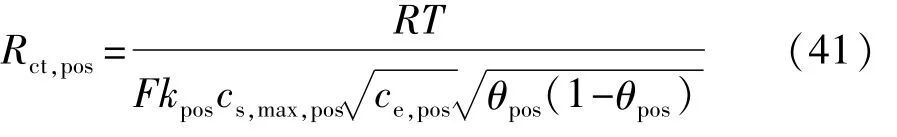
假设 θ100%，pos＝b，θ0%，pos＝a，定义 d＝a－b，代入式（39），则有 θpos＝a－dSOC，正极反应速率常数满足阿伦尼乌斯公式［14］：

式中：Ea为电极反应的活化能；Apos为指前因子。将式（42）和 θpos＝a－dSOC代入式（41），则可获得电池传荷电阻近似表达式：

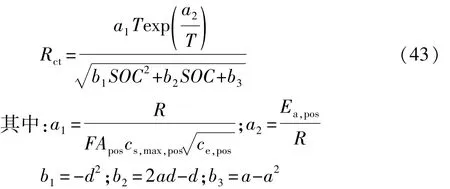
式（43）为传荷电阻与温度、荷电状态之间的关系式，若获得式中各个参数值，则可计算不同温度、荷电状态下的传荷电阻值。

2.1 不同状态下传荷电阻的折算

测量电池在不同状态下的电化学阻抗谱，分别分析电池传荷电阻随电池温度和荷电状态变化关系，就能确定传荷电阻表达式中的各个参数值。具体思路如下：调整电池荷电状态为SOCk，测量电池在不同温度下的EIS，与等效电路模型结合获得电池在该荷电状态、不同温度下的Rct。将式（43）中与电池荷电状态相关的表达项以P表示：

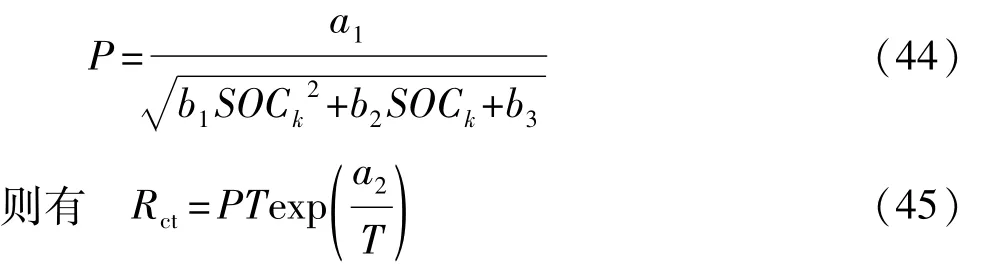
采用式（45）拟合电池荷电状态为SOCk时不同温度下的Rct，则能得到P和a2值。

同理确定 Q、b1、b2、b3，假设电池处于某一温度Tb，定义与温度相关项为Q：

则有

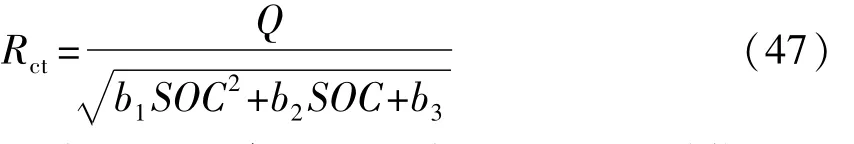
采用式（47）拟合电池温度为Tb时不同荷电状态下的 Rct，获得 Q、b1、b2、b3值。

确定 P、Q、a2、b1、b2、b3之后，将 SOCk代入 P或者Tb代入Q都可以解得a1，a1应同时满足式（44）和式（46）。由于设备存在测量噪声，两个表达式解得的a1会有差异。定义关于两个方程误差的目标函数J为

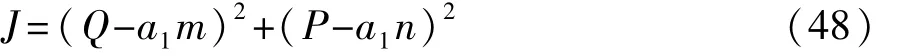
综上可知，电池不同状态下传荷电阻折算的关键是获得荷电状态为SOCk、温度为Tb时对应的a1、a2、b1、b2、b3，然后将不同温度和荷电状态值代入式（43）计算其它状态的传荷电阻值，从而实现不同温度和荷电状态下传荷电阻估计，下面对折算方法进行验证。

3 实验验证

同一批次编号为Cell1～Cell4的电池分别进行4种工况老化实验，充放电设备为 Chroma Model17011。电池容量标定采用0.5C电流充电，包含恒压阶段，充电截止电流0.055 A，放电电流1C，放电截止电压2.5 V，容量标定温度25℃。电池EIS测量使用Toyo BA500－50 Battery ANALYZER，电流幅值500 mA，频率10 kHz－0.01 Hz，实验过程如下：

（a）循环老化，Cell1和Cell2置于25℃恒温箱，使用0.5C电流充电至4.2 V，静置2 min，1C电流放电至2.5 V，循环25次，Cell3和 Cell4置于35℃恒温箱，使用0.5C电流充电至4.2 V，静置2 min，NEDC循环至电压小于2.5 V，充放电循环2次（NEDC循环25次）；

（b）将电池置于25℃恒温箱标定容量，然后采用恒流恒压充电至SOC达100%；

（c）采用1C倍率放电调整电池SOC为90%；

（d）依次设定恒温箱温度为35、25、15和5℃，电池在各个温度下静置1.5 h测量EIS，然后采用1C放电倍率让电池SOC下降20%；

（e）重复步骤（d），依次测量 SOC为90%、70%、50%、30%和10%在以上温度点的电池EIS；

（f）重复步骤（a）－（e），获得4节电池循环老化25、50、75、100、125次后的 EIS。

使用图5所示的等效电路模型解析不同状态下电池 EIS并得到电池传荷电阻［19－20］。

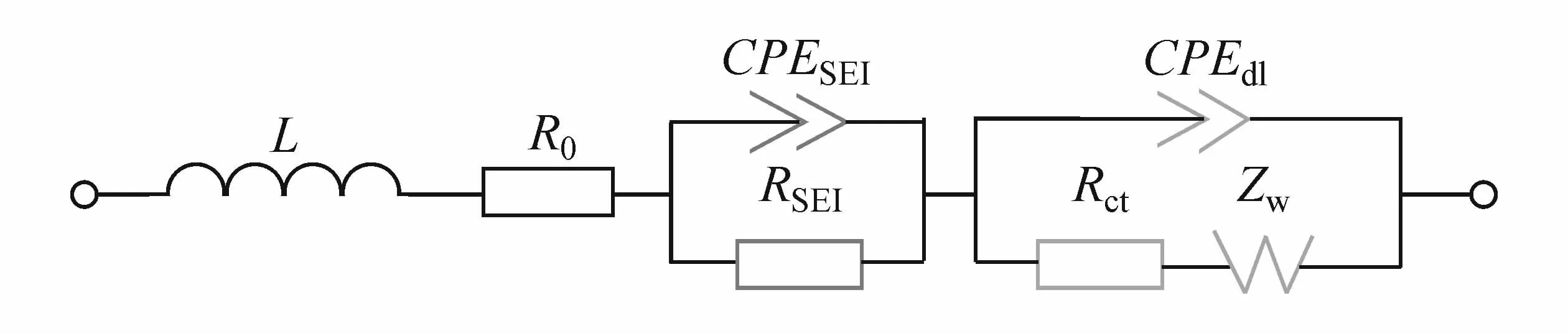
图5 电化学阻抗谱等效电路模型

Cell1循环25次不同状态下的EIS测量结果和4节电池循环25次后传荷电阻随温度与荷电状态的变化关系如图6～图9所示。

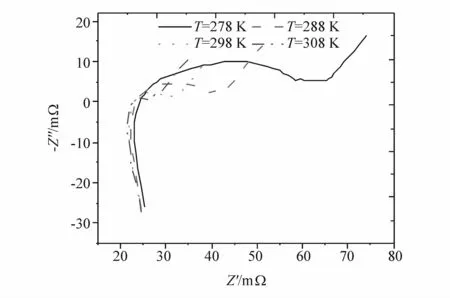
图6 Cell1循环25次SOC为50%时EIS随温度变化

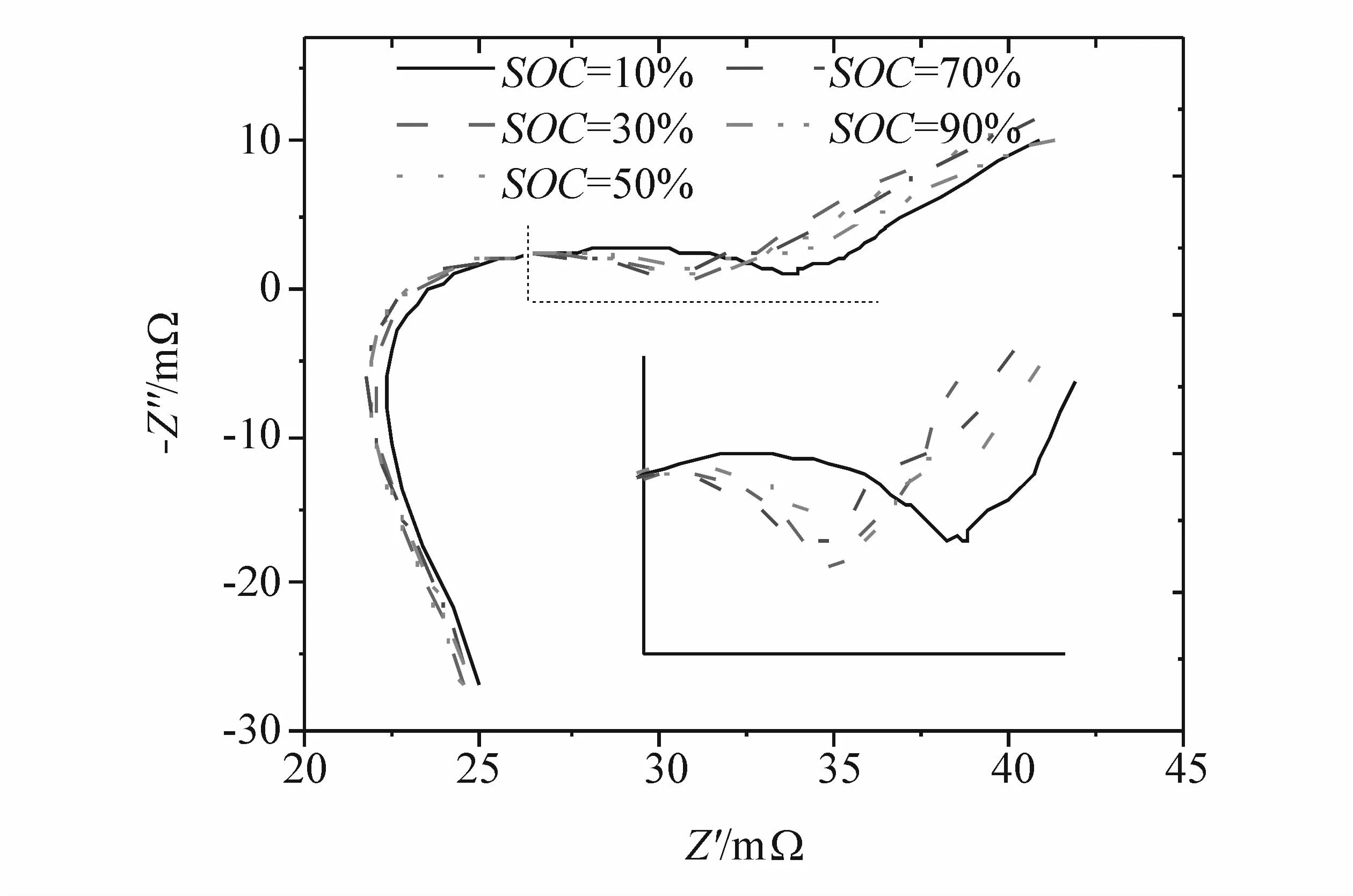
图7 Cell1循环25次25℃下EIS随荷电状态变化

图8 和图9中绘制了Cell1-Cell4循环老化25次后传荷电阻随荷电状态与温度变化关系，并用式（45）与式（47）去拟合获取式（43）参数值。由图8（a）～图8（c）可知传荷电阻随荷电状态呈现近似于抛物线变化关系，在荷电状态为50%附近传荷电阻有最小值。由式（41）正极传荷电阻表达式可知，正极传荷电阻在θpos为0.5时有最小值，将正极电化学工作窗口 θ0%，pos与 θ100%，pos代入式（39）求得正极传荷电阻取得最小值对应的荷电状态为SOCmin，pos＝58%，而从图7可知 EIS上反应传荷电阻的中低频圆弧半径在荷电状态为50%－70%区间内有最小值，两者结果相近。因此近似认为当正极传荷电阻达到最小值时电池传荷电阻也达到最小值，进一步说明使用正极传荷电阻代替电池传荷电阻合理性。

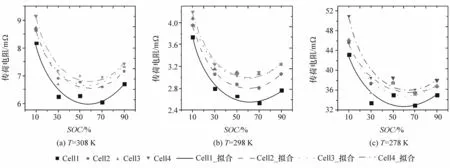
图8 Cell1-Cell4循环25次不同温度下的传荷电阻随荷电状态的变化（使用式（45）拟合）

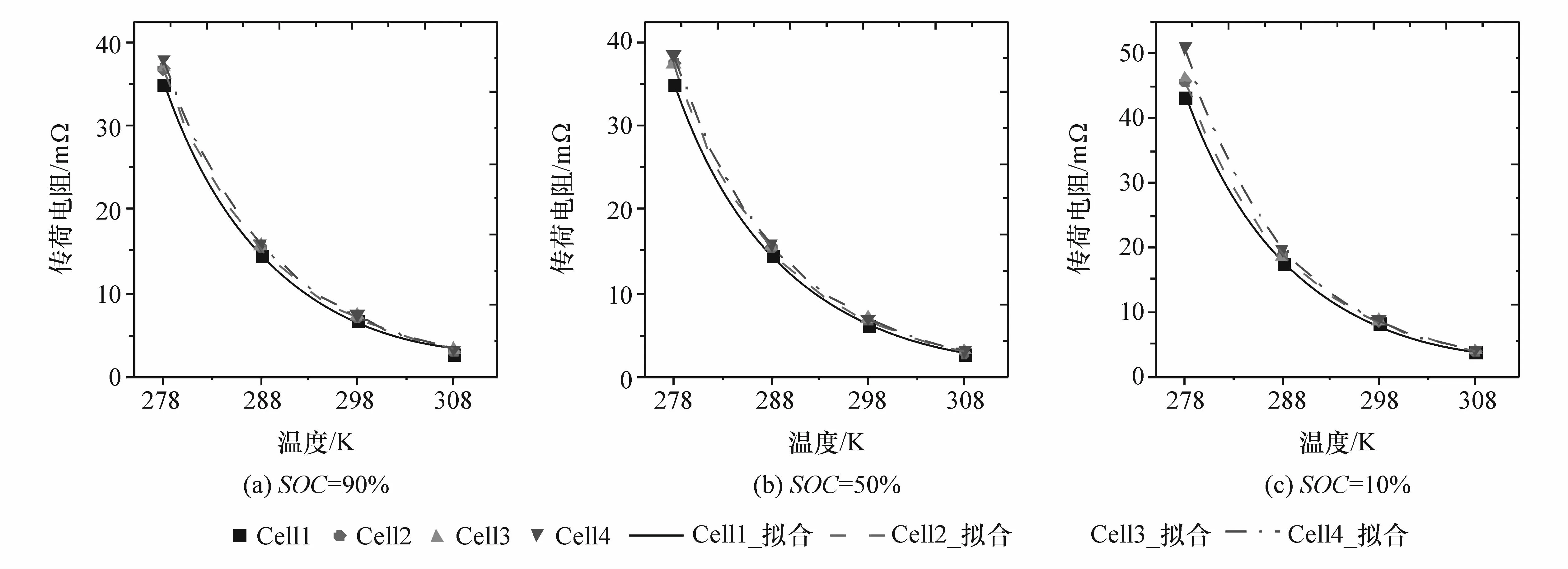
图9 Cell1-Cell4循环25次不同荷电状态下的传荷电阻随温度的变化（使用式（47）拟合）

获取电池不同循环系数不同状态下式（43）参数值后，接下来验证所提出的传荷电阻折算方法在电池各个状态和老化过程中的有效性。使用不同循环次数各个电池状态下参数值计算各个状态传荷电阻，以及与实验测量值的相对误差，然后计算相对误差平均值来表征传荷电阻折算方法在该电池状态下的误差。

记使用式（43）计算电池荷电状态为SOC、温度为T时传荷电阻值为（SOC，T）、实验测量值为（SOC，T），电池温度为 Tb、荷电状态为 SOCk时折算方法平均误差 δ定义，式中，下标 i表示SOC索引，j为温度索引，分母20代表电池有20个状态。不同老化工况电池Cell1-Cell4循环老化25、75、125次后各个状态的平均误差分布如图10～图13所示。

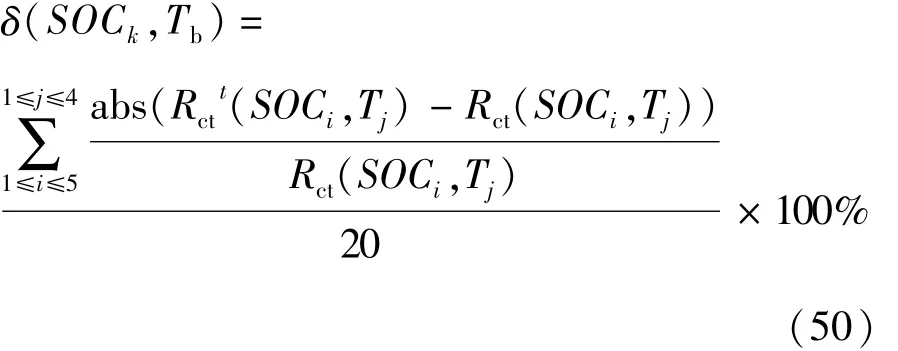
从图10～图13可知，不同循环老化工况电池Cell1-Cell4在老化过程中各个状态平均误差的最大值分别为8.98%、7.97%、7.85%、6.28%，且4节电池在绝大部分状态下误差分布均小于6%。误差来源主要有以下两个方面：首先传荷电阻应包含正负极上的传荷电阻，且所使用的传荷电阻表达式是线性化后的简化表达式；其次设备测量误差导致在电池中低频处测量得到的阻抗谱曲线有毛刺（图7），会影响拟合电化学阻抗谱所得到的传荷电阻值。

图10 Cell1不同老化阶段各个电池状态的平均误差分布

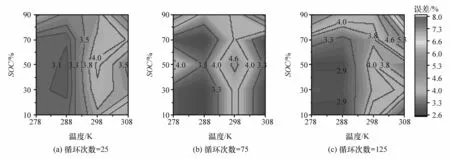
图11 Cell2不同老化阶段各个电池状态的平均误差分布

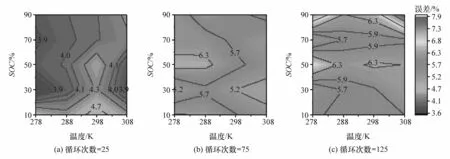
图12 Cell3不同老化阶段各个电池状态的平均误差分布

所提出方法可用于图14所示电池剩余寿命预测过程：在实车环境下根据式（43）计算电池荷电状态 SOC＝SOC0，温度 T＝T0时的传荷电阻T0）；假设电池状态 SOC＝SOC0，T＝T0时传荷电阻经验增长模型为 Rct＝g（α1，α2，…，αn，cycle）［4］，其中模 型 初 始 参 数。 然 后 基 于利用粒子滤波算法修正经验模型初始参数并结合电池失效时的Rct，end，计算电池剩余寿命RUL。

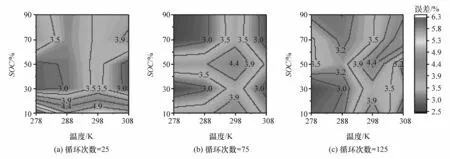
图13 Cell4不同老化阶段各个电池状态的平均误差分布

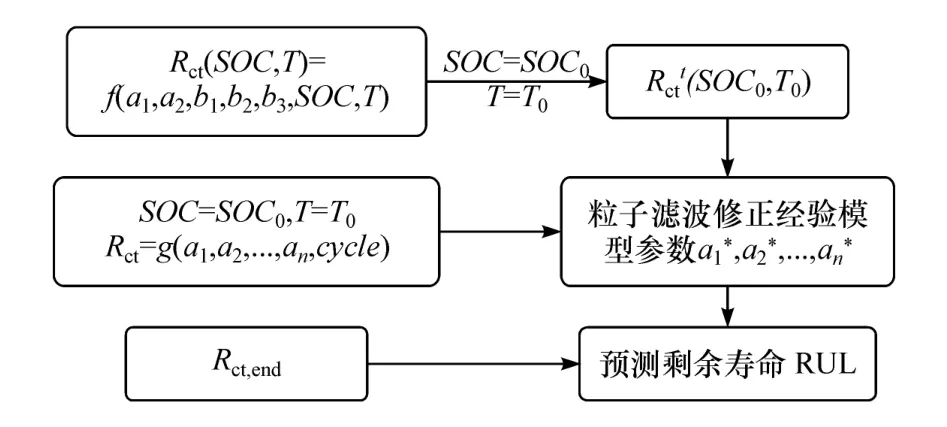
图14 电池寿命预测过程

4 结论

本文中从电池伪二维模型出发耦合负极SEI膜生成和正极活性材料损失的副反应模型，分析老化过程中正负极上传荷电阻的变化，基于仿真结果提出电池传荷电阻主要由正极决定的假设，推导了传荷电阻考虑温度和荷电状态的计算模型，阐述模型参数获取方法，并通过4种不同循环老化工况实验验证了在老化过程中各个状态下折算方法的有效性，为考虑电池不同温度和荷电状态下的剩余寿命估计提供基础。但也存在局限性：实验仅验证电池老化初期，对于电池后期衰减至0.8倍的初始容量老化过程需要进一步验证，同时缺乏对电池在全范围荷电状态和高低温的状态验证。