基于补偿滑模控制的混合动力汽车协调控制*

蔡英凤，窦 磊，陈 龙，施德华，汪少华，朱 镇

（1.江苏大学汽车工程研究院，镇江 212000； 2.江苏大学汽车与交通工程学院，镇江 212000）

前言

近年来随着汽车工业迅速发展，汽车保有量持续攀升，能源及环境问题日益凸显。为应对能源环境问题，各大汽车厂商不断探索降低油耗、减少排放的新技术，通过一系列发动机改进技术［1－2］、变速器技术［3］、车身设计［4－5］等手段来实现不同程度的整车节油效果。而混合动力汽车具有多个行驶模式，低速时可以在纯电动模式下行驶，中高速可以在发动机驱动模式或者混合驱动模式下行驶，可以减少发动机在非经济油耗区工作的机会，进而减少油耗和排放［6］，被认为是当前最具有发展潜力的节能汽车。

混合动力汽车在纯电动和混合驱动两个稳态工作模式之间的过渡过程是一个动态响应过程［7］，该过程涉及离合器接合、发动机快速起动、发动机和电机转矩切换。由于发动机和电机的响应速度不同以及离合器的非线性特性，导致动力系统输出的转矩会有较大波动，从而产生冲击，影响汽车行驶平顺性。

针对上述问题，清华大学的童毅［8］最先将混合动力汽车的控制分为转矩管理和动态协调控制，前者是控制混合动力汽车在什么时候进行状态切换以及各个状态下发动机和电机的目标转矩；后者对状态切换过程进行控制。文献［9］中利用最优控制原理，对单轴并联式混合动力汽车模式切换的各阶段发动机和电动机的目标转矩进行控制，但是忽略了发动机和电动机瞬态响应的差异。文献［10］中以单轴混联式传动机构为研究对象，提出了以纯电动模式下（离合器锁死）的电机转速为参考，通过设计相应的模型参考控制器，成功地控制了滑摩阶段的离合器两端转速跟踪参考转速，明显提升了切换平顺性。文献［11］中针对一种双模功率分流混合动力系统，探讨了其从输入功率分流模式切换到复合功率分流模式过程中变速器输出端转矩波动问题，并采用电机予以补偿，有效抑制了其转矩波动。文献［12］中采用模型预测控制方法，根据算法原理和适用性特征设计了面向离合器控制的模型预测控制器，基于控制目标分别选取了参考模型、预测模型和优化目标函数。文献［13］中设计了基于H∞的鲁棒控制器，进行分层协调控制，发动机侧控制器输入为发动机需求转矩，输出为发动机实际转速，通过实验验证了该策略能够较好地改善平顺性，具有较强的实用性和鲁棒性。

现有的协调控制方法大多数是通过对离合器接合过程的控制以达到协调控制的目的，但是离合器接合过程有较强的非线性，不可控制因素较多。控制过程中模型简化严重，都会建立理想的发动机、离合器转矩输出模型，但实际转矩控制、估计过程中存在很多时滞、超调、误差等情况，这就导致协调控制策略在实际应用时必须做出一定的修改和校正。

本文中以双行星排功率分流式混合动力汽车为研究对象，由于行星排结构的特殊性，可以通过调节任意两个构件的转速和转矩，使另一个构件转速转矩为0。因此结构上无需使用离合器，通过调节行星排转速和转矩来起到发动机平稳起步的效果。由于传动系统中没有离合器，简化了模型，省去了在建模过程中的诸多不确定因素。通过对切换过程进行动力学分析，建立基于滑模补偿的协调控制方法。确定模式切换过程中4个阶段：模式1，纯电动阶段1（制动器锁止）；模式2，纯电动阶段2（制动器断开）；模式3，发动机拖转；模式4，混合驱动。最后在Matlab／Simulink平台进行仿真验证，对该控制方法进行有效性分析。

1 功率分流式混合动力汽车动力系统结构及动力学分析

1.1 功率分流式混合动力汽车动力系统结构

本文中研究的功率分流式动力系统结构简图如图1所示，由发动机、发电机 MG1、电动机 MG2、制动器CB1／CB2和两个行星排组成。其中发动机与前行星排行星架相连，发电机MG1与前行星排太阳轮相连，电动机MG2与后行星排太阳轮相连。另外前行星排行星架与后行星排齿圈相连，前行星排齿圈、后行星排行星架、输出轴3者相连［14］。制动器CB1保证低速纯电动行驶时的效率，同时防止发动机对转速产生扰动；高速时制动器CB2锁死发电机MG1，提高效率，实现发动机直驱［14］。

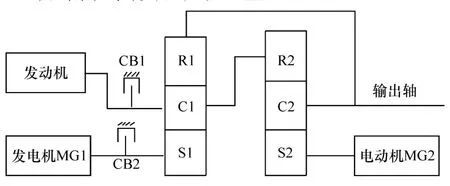
图1 动力系统结构简图

通过调节制动器分离和接合状态，纯电动到混合动力切换过程分为4个过程，各部件状态如表1所示。

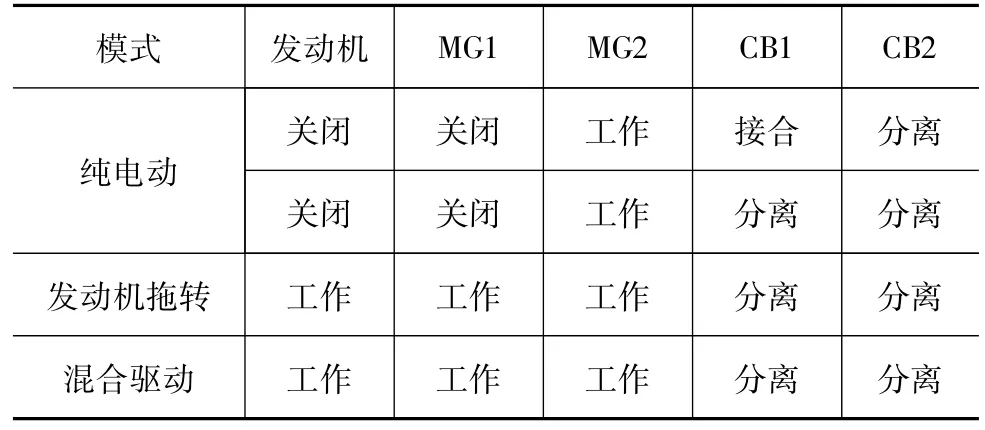
表1 功率分流式混合动力汽车模式划分

汽车以纯电动模式起步，当运行负荷较小，转速较低时，保持纯电动模式运行；运行一段时间后由于加速或者爬坡导致运行负荷增大，需要切换到混合驱动模式。在此过程中，MG2持续输出需求转矩，制动器CB1断开，使发动机在0.4 s内点火起动，随后输出需求转矩。由于发动机的响应过程较慢，电动机响应速度快，因此，在发动机响应过程中会产生转矩的波动，这就需要MG1、MG2对发动机进行转矩补偿，保证车辆平稳运行。

1.2 模式切换过程动力学模型

1.2.1 车辆系统动力学模型［15］

根据牛顿力学方程建立整车纵向动力学数学模型，汽车驱动力-行驶阻力平衡方程为

式中：Ftrac为驱动力；Ff为滚动阻力；Fw为空气阻力；Fi为坡度阻力；Fa为加速阻力。

滚动阻力、空气阻力、坡度阻力、加速阻力分别为

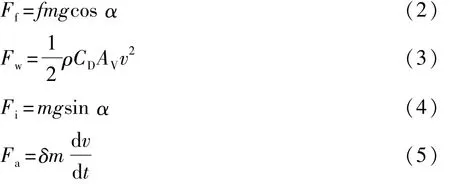
式中：m为整车质量；g为重力加速度；α为路面倾角；ρ为空气密度；CD为空气阻力系数；AV为迎风面积；v为车速；f为路面摩擦因数；δ为旋转质量换算系数为行驶加速度。

1.2.2 各行星排转矩平衡方程

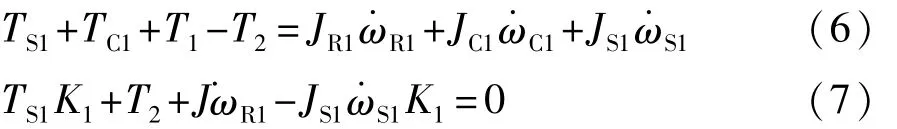
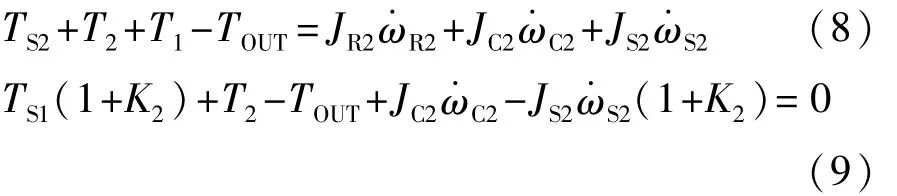
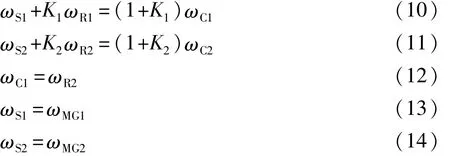
转速平衡关系为式中：TS为太阳轮转矩；TC为行星架转矩；T1为行星排1的行星架到行星排2的齿圈的转矩；T2为行星排1的齿圈到输出轴转矩；TOUT为输出转矩；JR齿圈转动惯量；JC为行星架转动惯量；JS为太阳轮转动惯量；ωS为太阳轮角速度；ωR为齿圈角速度；ωC为行星架角速度；ωMG1为电机1角速度；ωMG2为电机2角速度；K1、K2为前后行星排传动系数。

1.2.3 各模式下的转矩分配公式

纯电动阶段1：

纯电动阶段2：

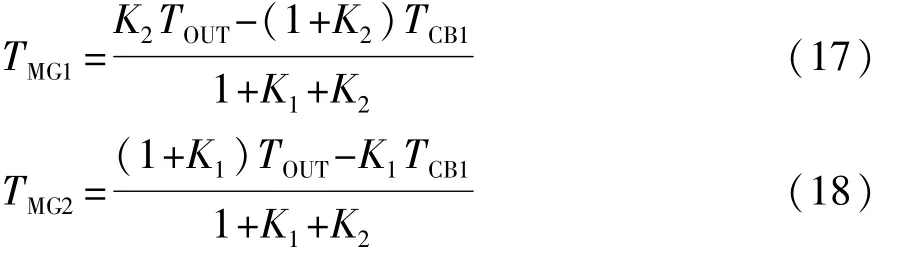
发动机拖转阶段：

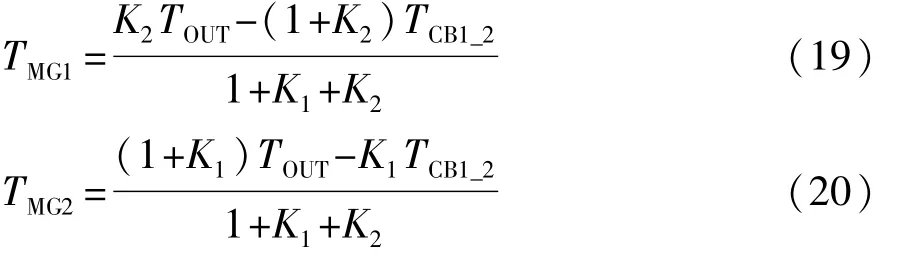
混合动力阶段：

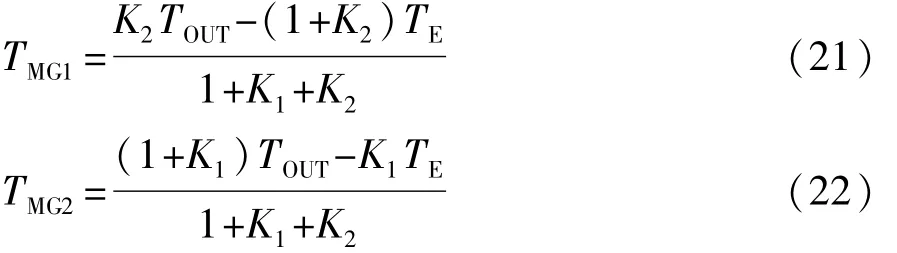
式中：TMG1为电机1转矩；TMG2为电机2转矩；TCB1为制动器CB1转矩；TCB1＿2为起动发动机所需要转矩；JE为发动机转动惯量；TE为发动机输出转矩。

1.2.4 各阶段传动系统模型

纯电动阶段1和纯电动阶段2：

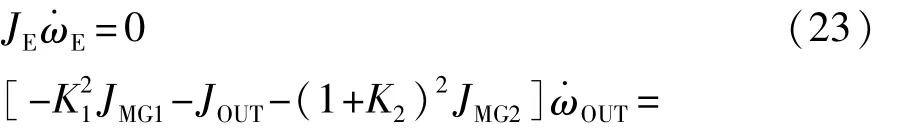
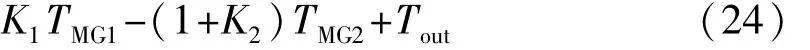
发动机拖转：

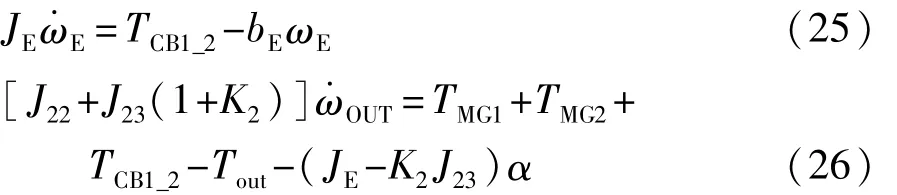
其中：

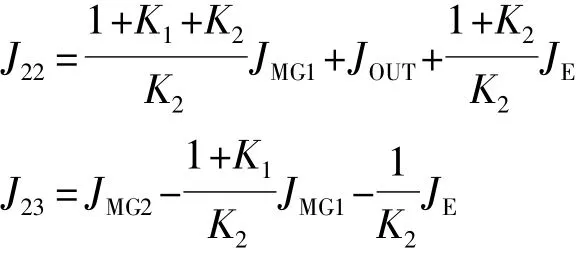
混合驱动阶段：

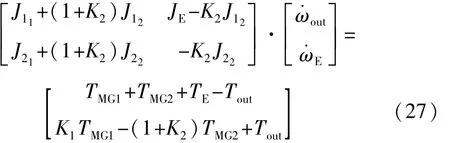
其中：

式中：JMG1、JMG2为电机 MG1、MG2的转动惯量；ωE为发动机角速度；bE为发动机阻力系数；ωOUT为输出轴角速度。

2 模式切换协调控制策略

整车模式切换协调控制流程如图2所示。车辆起步后，整车负荷较小，汽车以纯电动模式行驶。当驾驶员的需求转矩Treq大于纯电动模式所能输出的最大转矩 TEV＿max或电池 SOC小于电池最低阈值SOCmin或需求车速v大于纯电动所提供的最大车速vEV＿max时，整车控制器接收模式切换信号，控制制动器CB1迅速打开，同时进行MG1、MG2的协调控制。等制动器CB1完全打开后，MG1拖转发动机，同时MG2对拖转发动机所造成的转矩损失进行补偿。当拖转发动机转速nICE大于发动机怠速转速nidle后发动机点火，进入混合驱动模式。此时发动机转速迅速从怠速转速增长到1 500 r／min的经济转速，但由于发动机瞬态转矩反应的滞后，使发动机不能及时到达目标转速，利用MG1、MG2进行转矩补偿，补偿值通过滑模控制器求解，以满足驾驶员的需求转矩，降低输出端的转矩波动，减少车辆冲击。

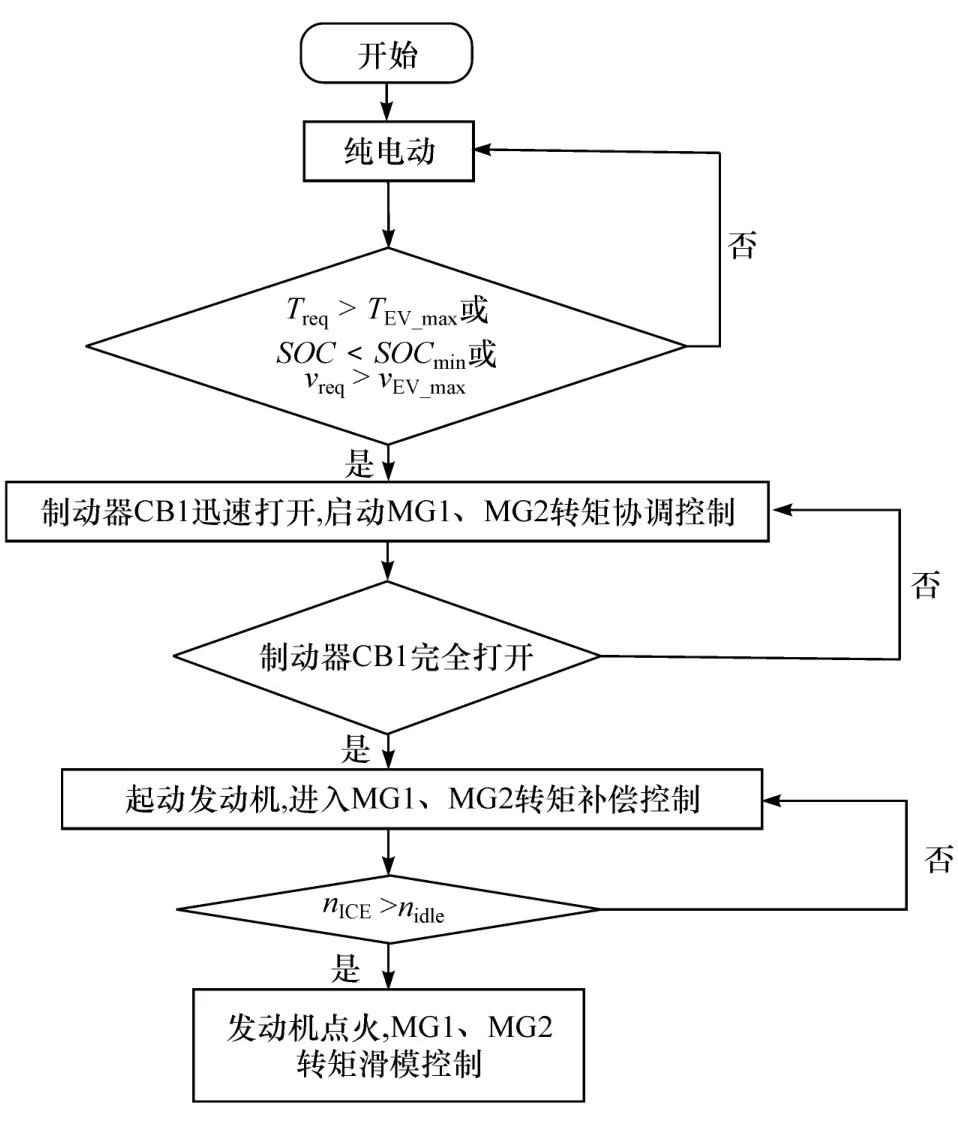
图2 模式切换协调控制流程图

2.1 发动机拖转阶段的转矩补偿控制［16］

制动器CB1完全打开后，电动机MG1开始拖转发动机，此时，MG1的实际输出转矩TMG1需要在纯电动模式输出转矩的基础上添加拖转发动机所需要的转矩T′MG1，同时电动机MG2的实际输出转矩TMG2需要在纯电动模式输出转矩的基础上添加补偿转矩T′MG2，用以消除MG1拖转发动机对输出轴转矩的影响。此阶段系统的控制框图如图3所示。

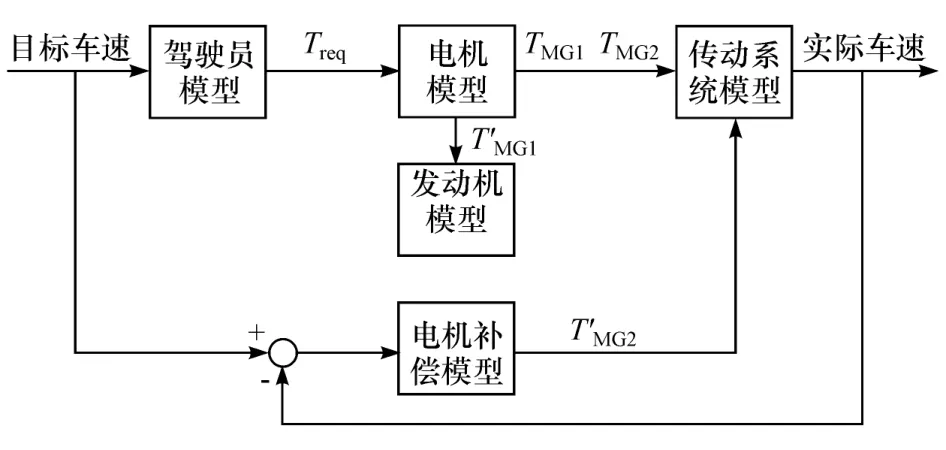
图3 发动机拖转阶段控制框图

转矩补偿前电机MG1、MG2的转矩分别为稳态时转矩分配公式，如式（19）和式（20）所示，没有考虑发动机起动时的阻力矩和转动惯量。考虑补偿后，该阶段电机MG1、MG2的目标转矩分别为

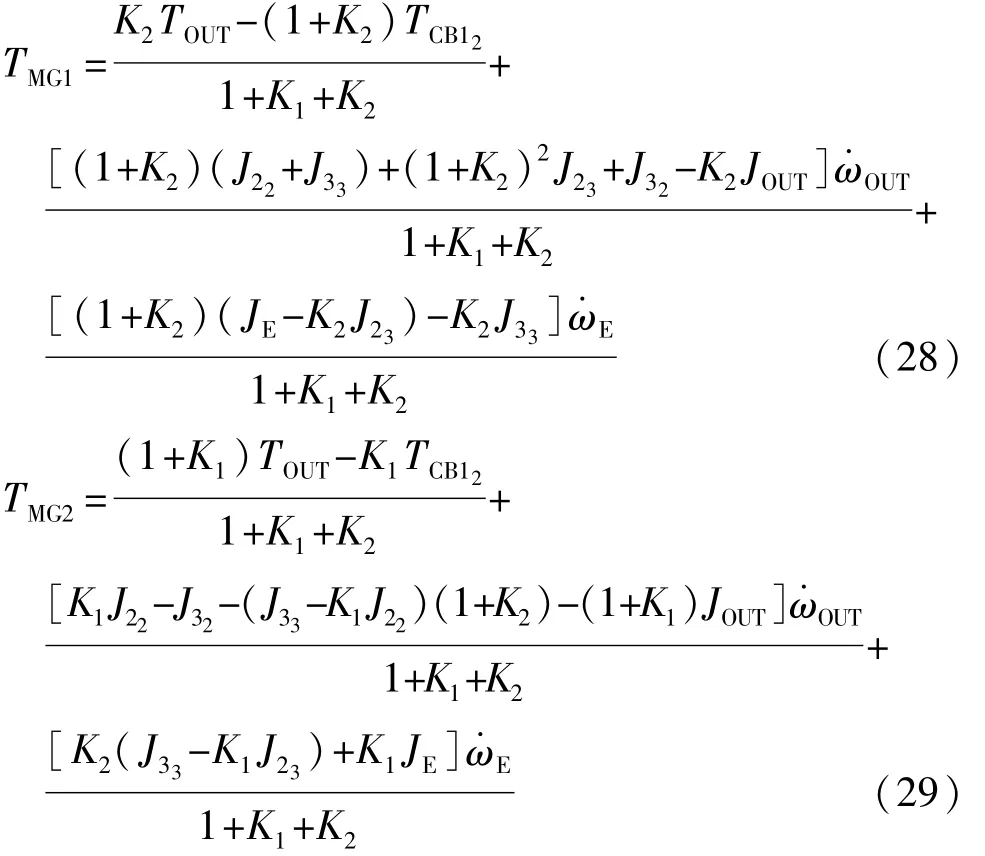
2.2 混合驱动阶段的滑模控制

发动机的转速达到怠速后，发动机点火起动，此时发动机、MG1、MG2同时向传统系统输出转矩，驱动车辆行驶，汽车处于混合驱动阶段。但由于发动机的转矩瞬态响应较慢，无法和电机一样瞬间到达理想状态，因此需要对所估算出的发动机实际转矩，利用MG1、MG2对发动机转矩不足进行补偿。文中利用滑模控制，计算出补偿量，然后进行补偿。此阶段的控制目标是完成模式切换，实现与纯电动模式“无缝”切换。汽车进入混合驱动阶段后的目标行驶状态应该与车辆保持纯电动模式的行驶状态一致［17］。此阶段系统的控制框图如图4所示。

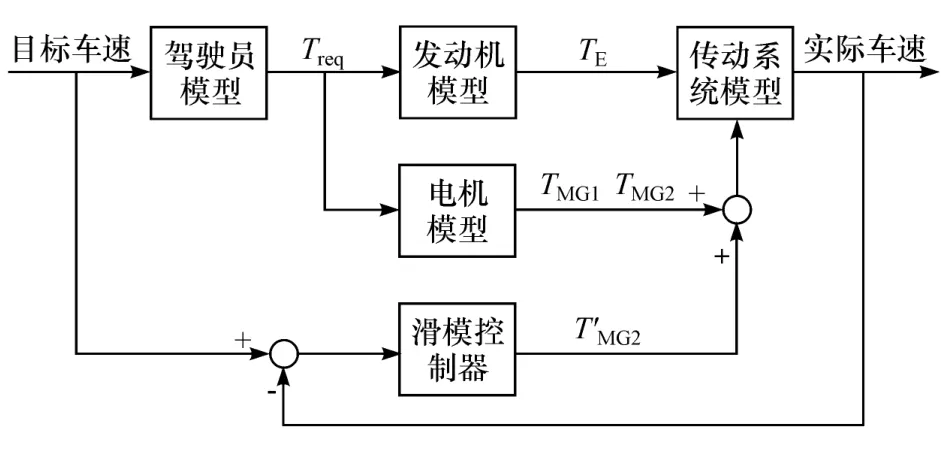
图4 混合驱动阶段控制框图

此阶段采用基于固定边界层的自适应滑模控制，通过建立一个切换超平面，并构造一个控制规律，来使控制目标满足条件，使切换平面以外的点都慢慢到达切换面并滑向原点。当系统到达滑模状态后，跟踪误差趋近于零。但是系统状态到达切平面后，难以严格按照指定切平面滑向原点，会在切平面两侧来回穿越，产生颤振，影响系统稳定性。因此，本文中为消除颤振所设计的滑模控制器采用固定一定厚的边界层，其在切平面附近定义一个较薄的边界层，使得输入控制在边界层外部采用切换控制，使系统快速趋于滑动模态，边界层内部采用反馈控制，降低滑动模态迅速切换所导致的颤振。

将车辆需求车速和实际车速的偏差值和系统参数的不确定性引起的偏差视做系统的干扰项。混合驱动阶段纵向动力学模型为式（27），进入混合驱动阶段后，通过调整MG2的转矩实现对应的控制目标。因此，此阶段混合动力系统输出轴端的动力学方程可重写为

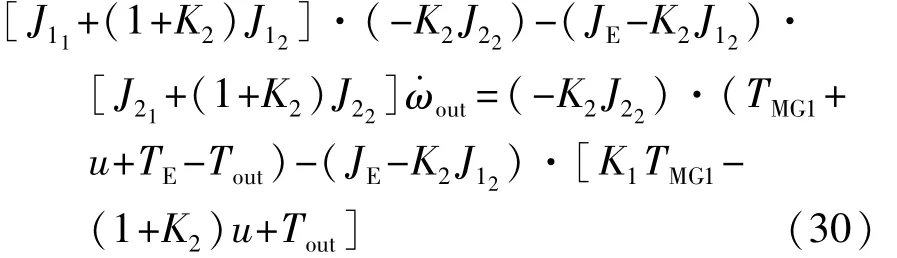
式中u为滑模控制器的控制律。

（1）滑模切换超平面设计

定义跟踪误差：

式中：ωreq为车辆需求的输出轴角速度；ωout为车辆实际输出轴角速度。

滑模切换超平面：

式中λ为正常数。

（2）滑模控制器设计

当系统处于滑模运动时，满足S·（t）＝0，可得

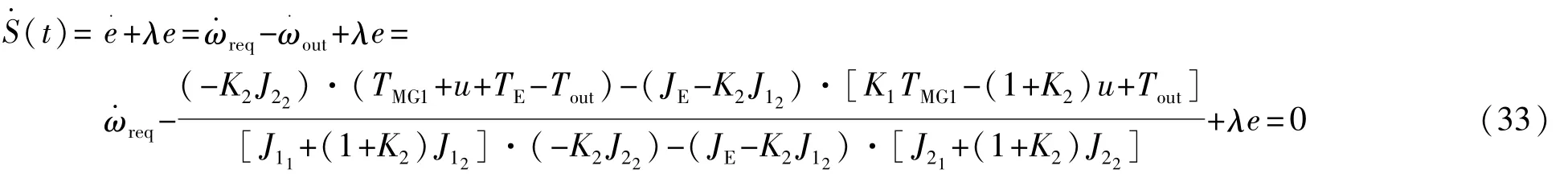
得到此阶段滑模控制等价控制律u为

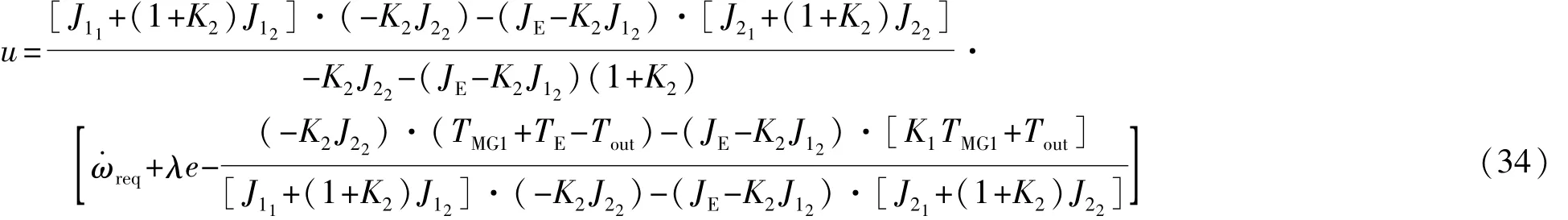
为消除颤振，滑模控制的到达控制采用基于sat函数的固定边界层滑模控制，sat函数定义［18］见式（35），式中，k＝1／Δ，Δ为边界层。

根据式（34）和式（35），在该模式下的协调控制律见式（36），式中η为正常数。

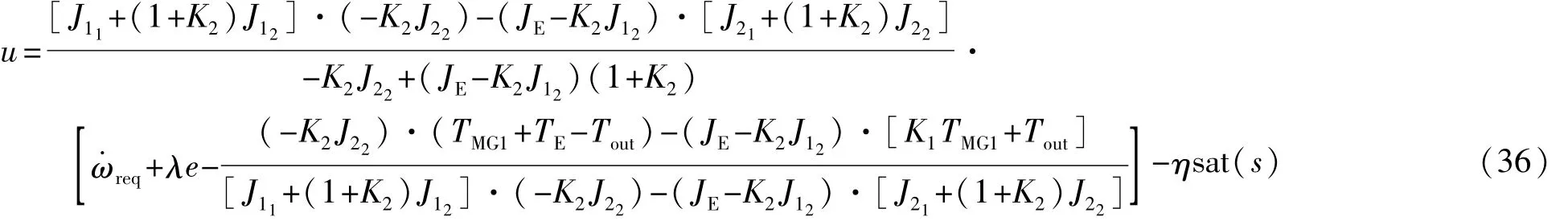
（3）稳定性分析

构造Lyapunov函数：

对Lyapunov函数两边同时求导：

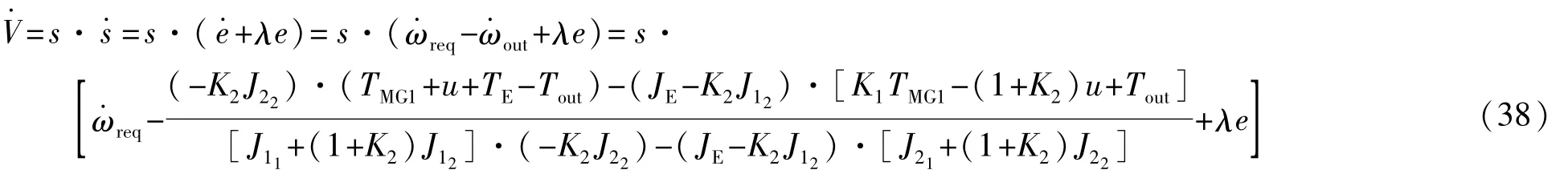
将式（36）代入上式得

3 仿真结果及分析

利用Matlab／simulink仿真平台搭建功率分流式混合动力汽车前向仿真模型及转矩协调控制模型进行仿真验证。

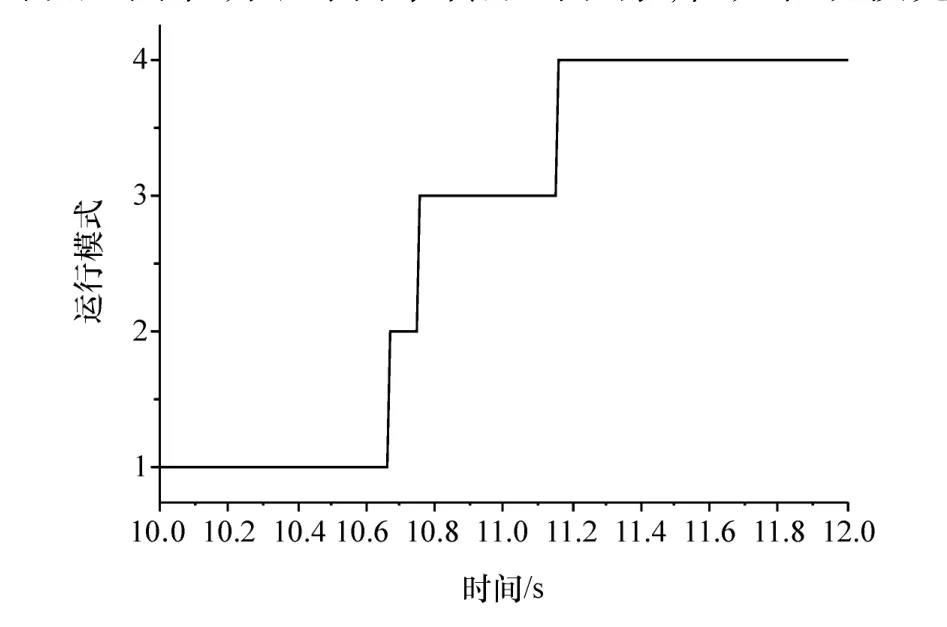
图5 运行模式

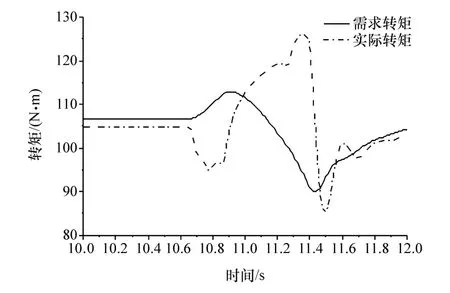
图6 驾驶员需求转矩与实际转矩

图5 为汽车由纯电动到混合驱动运行模式的切换过程，由图可知，整个切换过程基本控制在1 s左右，切换过程能够迅速完成。图6为汽车行驶过程中需求转矩与实际转矩的对比，汽车在模式切换过程中有发动机转矩引入过程，导致需求转矩出现波动，为跟踪目标车速，需要调节实际转矩，因此会出现无法准确跟踪需求转矩的现象，但是在切换完成后能够及时调整，重新跟踪需求转矩。图7为实际车速与需求车速的对比，由图可知车速的跟踪效果良好，基本能够满足车速需求。图8为控制前后发动机转速对比，控制前发动机转速变化剧烈，且点火时出现发动机转速降低的现象，通过进行补偿滑模控制，发动机转速变化过程趋于平缓，且没有转速波动现象，达到经济转速1 500 r／min的时间较短。图9为控制前后冲击度对比，控制前后冲击度发生显著变化，冲击度改善明显，整个过程冲击度均没有超过德国冲击度限值10 m／s3。图10为发动机实际与需求转矩对比，图11和图12为控制前后MG1、MG2的转矩对比。由图可见：发动机转矩跟踪效果较好，且时间较短；MG1、MG2较控制前在切换过程中转矩变大，这是由于补偿滑模控制通过MG1、MG2进行转矩补偿，变大的部分为补偿值。

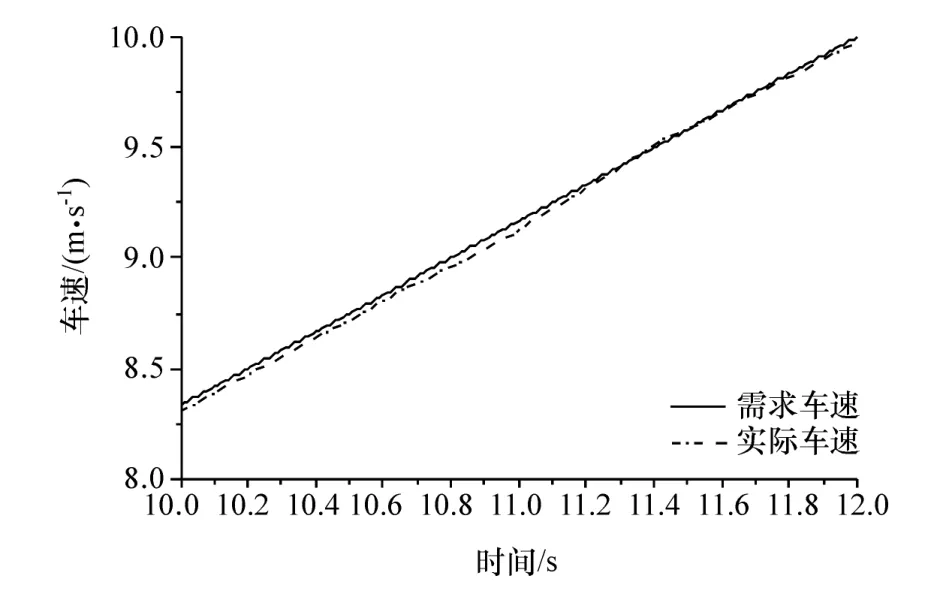
图7 驾驶员需求车速与实际车速

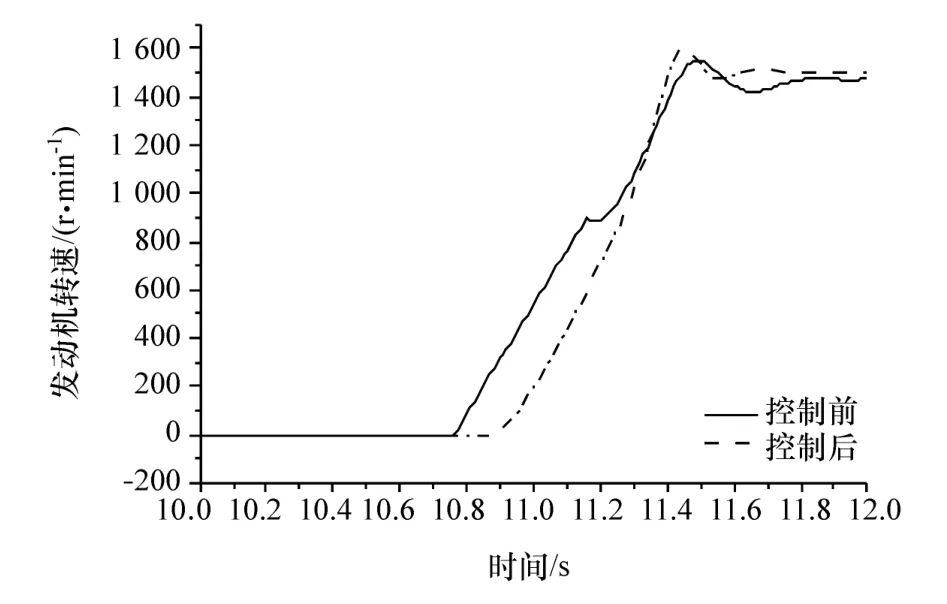
图8 控制前后发动机转速对比

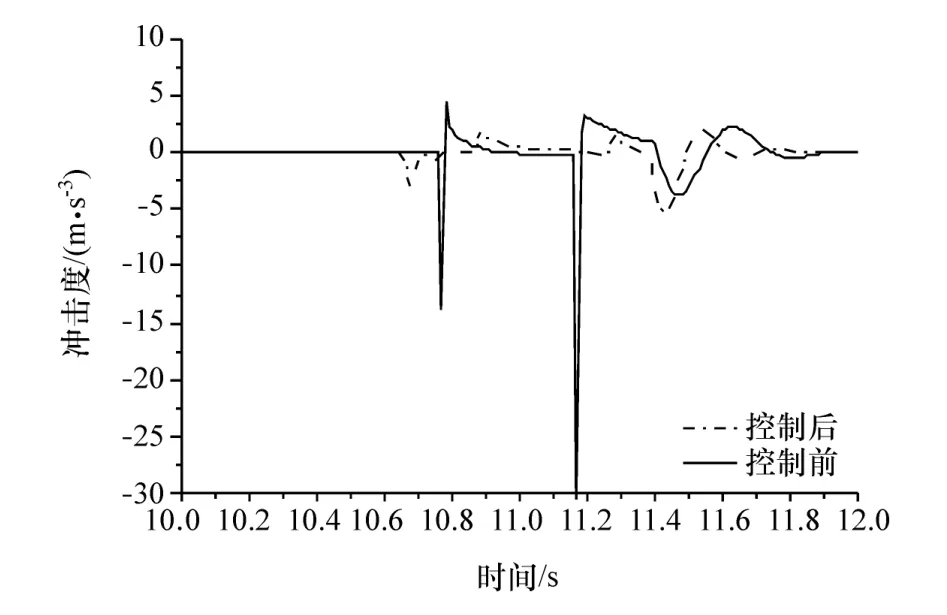
图9 控制前后冲击度对比

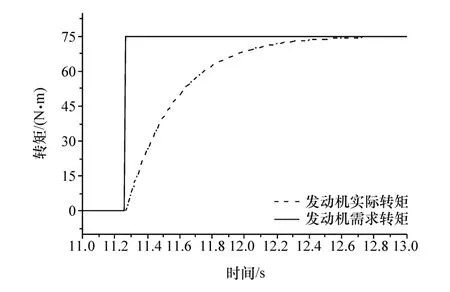
图10 发动机实际与需求转矩对比

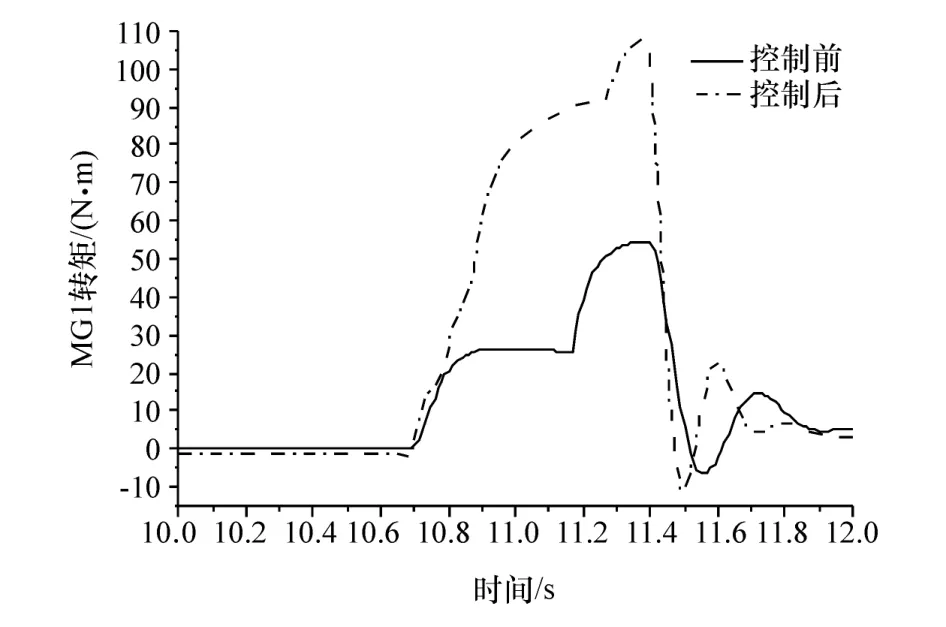
图11 控制前后MG1转矩对比

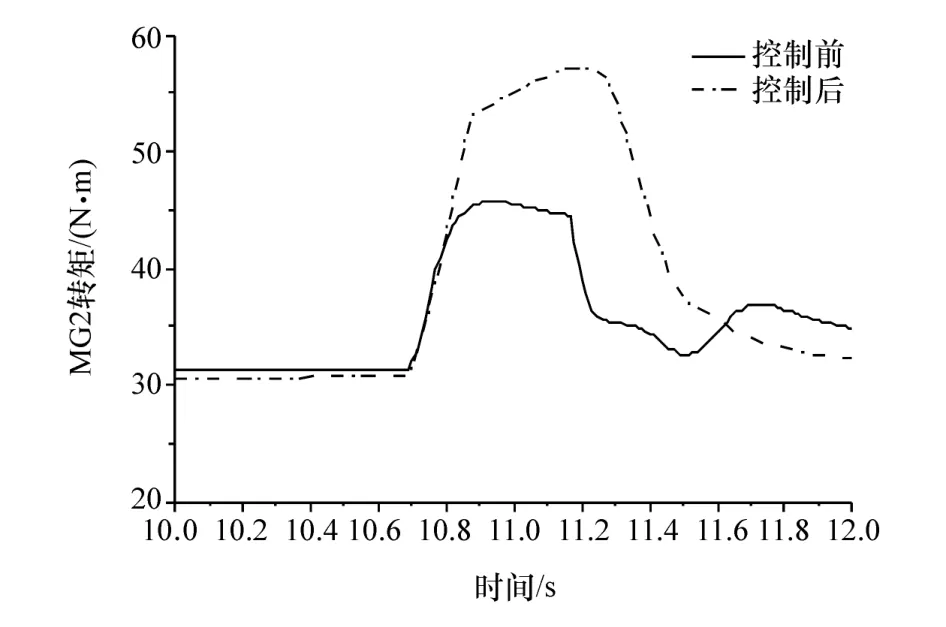
图12 控制前后MG2转矩对比

仿真结果表明，基于补偿滑模控制的模式切换协调控制策略能够有效地降低输出端转矩波动，减小冲击度，能够在满足驾驶员行驶需求的前提下，提高驾驶平顺性，改善驾驶体验。

4 结论

（1）建立功率分流式混合动力汽车动力系统的瞬态动力学模型，求得每个模式下理想状态的转矩分配，以此来获得每个动力源对应的目标转矩。

（2）将从纯电动到混合驱动模式切换过程中的发动机拖转和混合驱动模式进行单独的控制。对发动机拖转阶段采用电机补偿控制，通过对MG1、MG2添加补偿转矩，以此来抑制发动机起动过程所引起的转矩波动；混合驱动阶段采用基于固定边界层的自适应滑模控制，来消除由于发动机的转矩瞬态响应较慢，无法和电机一样瞬间到达理想状态所引起的转矩波动，同时通过固定一定厚的边界层，用来消除滑模控制过程中可能引起的颤振。

（3）整个切换过程采用的转矩协调控制策略能够有效地减小切换过程的转矩波动和传动系统的冲击，提高了车辆行驶的平顺性。