隧道变形引起的钢弹簧浮置板轨道变形与脱空分析

程霖，杨成永，马文辉，车敬珂

隧道变形引起的钢弹簧浮置板轨道变形与脱空分析

程霖1，杨成永1，马文辉1，车敬珂2

(1. 北京交通大学 土木建筑工程学院，北京 100044；2. 北京市市政工程设计研究总院有限公司，北京 100082)

穿越施工引起既有隧道及其上的轨道结构产生变形，给列车运营安全带来不利影响。将钢弹簧浮置板轨道视为弹性地基梁，建立钢弹簧浮置板轨道变形的控制微分方程。采用傅里叶级数法求解微分方程，得到关于未知级数系数的线性方程组，进而给出求解线性方程组的迭代方法。基于本文方法分析钢弹簧浮置板轨道与隧道底板相互作用规律。研究结果表明：浮置板自身的抗弯刚度使其与隧道底板存在变形差异，进而与隧道底板产生脱空；随着隧道底板变形的增大，轨道结构变形及脱空范围均增大；随着沉降槽宽度的增大，轨道变形与隧道底板逐渐趋近，脱空范围呈先增大后减小的趋势；钢弹簧刚度越大，间距越小，轨道与隧道底板越容易产生脱空，脱空范围越大。研究成果可为穿越施工中既有线轨道结构的安全评价提供理论依据。

穿越施工；钢弹簧浮置板轨道；变形；脱空；傅里叶级数解

随着城市轨道交通建设规模的扩大，不可避免出现新建地铁隧道穿越既有隧道的现象[1]。新建隧道施工引起既有隧道底板及其上的轨道结构产生变形[2−4]，进而影响既有线的运营安全。轨道结构与隧道底板不是一个整体，在新建隧道施工影响下，两者变形存在差异，甚至产生脱空。例如，北京地铁5号线下穿地铁2号线施工过程中，既有2号线道床板与隧道底板在变形缝两侧产生脱空，最大脱开值达12.7 mm[5]。然而，目前在穿越工程轨道结构力学计算时，大多将既有轨道与隧道底板变形视为等同，忽略两者的相互作用[6−7]，这样得到的计算结果并不能反映实际情况。常见的轨道结构计算模型包含弹性地基梁模型、弹性地基梁−板模型和梁体模型3类。张群[6]建立了双块式无砟轨道的弹性地基梁−板有限元模型，分析了道床板和支承层的受力特性。赵坪锐等[7]建立了无砟轨道的弹性地基梁有限元模型，分析了梁端位移、梁端悬臂长度等因素对扣件系统受力的影响。孙璐等[8]分别采用弹性地基叠合梁模型、弹性地基梁−板模型、梁体模型3种模型计算了板式无砟轨道的受力情况。以上计算模型描述了轨道结构各部分之间的关系，但均未对轨道与下伏支承结构的相互作用问题进行研究。轨道与隧道底板相互作用问题具有复杂性。轨道与隧道底板产生变形差异后可能出现脱空区，轨道在脱空区和接触区承担的荷载不同，目前尚无有效的理论方法能够考虑轨道与隧道底板的脱空。本文针对城市轨道交通中应用较为广泛的钢弹簧浮置板轨道建立理论分析模型。将浮置板道床视为弹性地基梁，建立了轨道变形控制微分方程，引入“相当荷载”[9]模拟相邻浮置板间的剪力铰，引入阶梯函数描述浮置板道床与隧道底板的脱空。用傅里叶级数解法对控制微分方程进行了求解。将本文方法的计算结果与数值模拟结果进行对比，验证了本文方法的正确性，进一步讨论了钢弹簧浮置板轨道与隧道底板的相互作用规律。

1 控制微分方程及边界条件

钢弹簧浮置板轨道由钢轨、扣件、浮置板、钢弹簧隔振器、剪力铰等部件构成。钢轨通过扣件固定在浮置板上，浮置板由钢弹簧隔振器支承在隧道底板上，相邻浮置板由剪力铰相连。剪力铰具有较大的径向刚度，可避免钢轨受到过大的剪力[10]。

将地铁隧道开挖引起的既有隧道变形作为荷载施加到轨道结构上，并采取以下假设：

1) 浮置板道床与钢轨变形一致，两者简化为单层弹性地基梁，变形服从平截面假定，基底变形遵从Winkler假定。2) 钢弹簧隔振器提供的点支承刚度等效为连续支承刚度。3) 相邻浮置板通过剪力铰铰接，剪力铰不传递弯矩。

由以上假设得到理论计算模型如图1所示。模型中轨道结构关于轴对称，计算范围是[−，]，分布荷载−()为对称荷载。

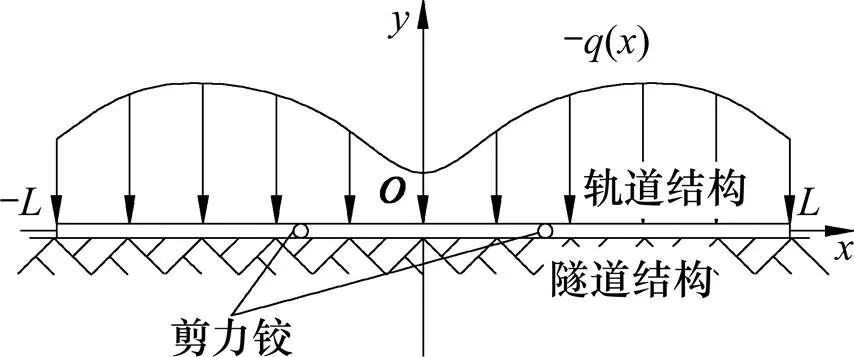
图1 钢弹簧浮置板轨道计算模型

轨道结构变形的控制微分方程为[11− 12]

式中：为轨道结构的弹性模量；为轨道结构横截面的惯性矩；()为轨道结构竖向变形，向上为正；为沿轨道轴向的坐标；()为右端荷载，向上为正。

轨道结构两端位于隧道开挖的影响范围之外，轨道结构两端(=±)转角为0，即

2 相当荷载和阶梯函数

2.1 相当荷载

传统弹性地基梁法只能求解连续刚度梁，不能考虑铰接，因此本文在剪力铰两侧的极小区域内施加“相当荷载”。相当荷载为分布荷载，可简化为一对大小相等，方向相反的力偶。相当荷载自身构成平衡力系，不影响整体的平衡，但能够迫使梁转角在相当荷载施加处产生突变，如图2所示[9]。

图2 相当荷载使梁产生相对转角(h为无限趋近于0的数)

相当荷载的表达式为

式中：q()为相当荷载，向上为正；Δ为相对转角，以铰接点右侧梁段相对于左侧逆时针转动为正；″(0)为脉冲函数的二阶导数；0为铰接点位置。

相当荷载相当于在铰接处施加了额外弯矩，故铰接处有以下荷载边界条件

式中：M(0)为q()在=0处产生的额外弯矩。

2.2 阶梯函数

隧道底板发生竖向变形前，在钢轨、浮置板道床重力的作用下，钢弹簧产生初始压缩量。隧道底板产生竖向变形后，浮置板道床与隧道底板沉降差超过钢弹簧的初始压缩量，钢弹簧恢复原长，不再提供支承力，本文称之为轨道与隧道底板产生脱空。在脱空区，轨道结构只受到重力作用；在接触区，轨道结构受到重力和地基反力的共同作用。

综上，式(1)中右端荷载()包含轨道自重、地基支承反力和相当荷载，可写为

式中：为重力加速度；为轨道线密度；为浮置板道床宽度；为地基系数(若钢弹簧刚度为k，间距为l，则=k/(bl))；()为轨道与隧道底板竖向位移差，若隧道底板位移为()，则()=()−()。在式(5)中引入阶梯函数：

将式(5)代入式(1)，则控制微分方程可写为：

轨道与隧道底板的脱空点为函数()的零点。每个脱空区间包含2个端点，因此()的零点个数为脱空区间个数的2倍。由于荷载和结构的对称性，()关于轴对称，()的正根个数正好等于脱空区间个数。若轨道与隧道底板存在个脱空区，则()在区间[0,]上的正根从左到右依次为1，2，…，e，式(6)在区间[0,]上可写为如下2种形式：

当为奇数时，

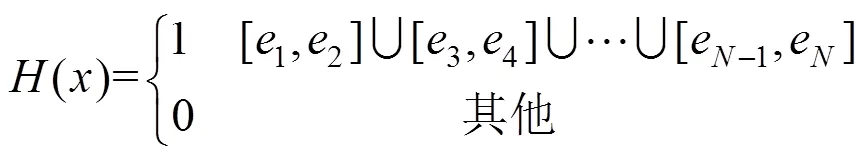
当为偶数时，

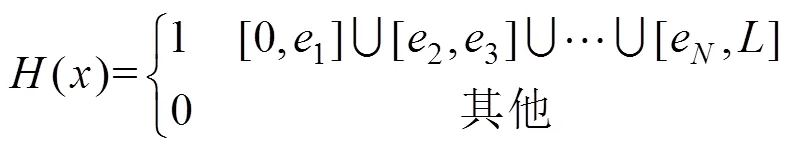
3 傅里叶级数解法

3.1 未知函数的级数展开

式(7)中，轨道结构变形()和阶梯函数()为未知函数。

将()展开为余弦级数，即：

式中：0和a为待求的傅里叶级数的系数。

将()在[−,]内展开成余弦级数，即：

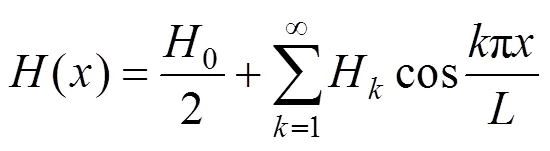
式中：0和H为傅里叶级数的系数。

根据式(8)和式(9)，若轨道与隧道底板存在个脱空区间，有

3.2 已知函数的级数展开

式(4)和式(7)中，隧道底板变形()，脉冲函数(x−x)及其二阶导数(x−x)为已知函数。

假定隧道底板变形符合Peck曲线[13]，即：

式中：0为隧道底板最大变形，发生在=0处；为沉降槽宽度。

将()展开为余弦级数，即：

式中：0和b为傅里叶级数的系数。

脉冲函数的表达式为

将(0)展开为余弦级数，即：

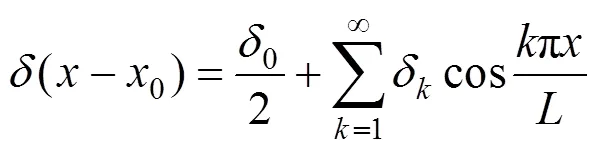
式中：0和δ为傅里叶级数的系数。

将(0)展开为余弦级数，即：

将上述已知函数的级数系数列于表1。

3.3 系数方程组及其求解

根据傅里叶级数的乘法法则计算式(7)中阶梯函数()与()及()的乘积。

表1 已知函数的傅里叶级数系数

()与()乘积()的余弦级数为：

式中：0和β为傅里叶级数的系数；|×|表示绝对值。

()与()乘积()的余弦级数为：

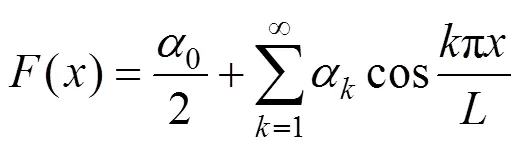
式中：0和α为傅里叶级数的系数。

将式(10)，(18)，(19)，(22)，(23)和(24)代入式(7)，比较系数并取级数前项，可得线性方程组：

式(25)即为确定待定系数0和a的方程组，包括+1个方程，但含有0~a，1~e以及Δ共++2个未知数，需要进行迭代求解。

首先令相对转角Δ=0，先迭代脱空。第1次迭代假定轨道与隧道底板不产生脱空，可通过式(25)求得系数0(1)~a(1)(括号中数字代表迭代次数)；将0(1)~a(1)代入式(10)，求得()零点的第1次迭代值1(1)~e(1)；第2次迭代将1(1)~e(1)代入式(25)求得0(2)~a(2)，进而通过式(10)计算得到()零点的第2次迭代值1(2)~e(2)；以此类推直至前后2次迭代计算的()零点符合精度要求为止。

脱空迭代完成后，迭代转角Δ。此时()零点1~e为已知。将式(10)和(17)代入式(4)，得到如下的转角计算公式：

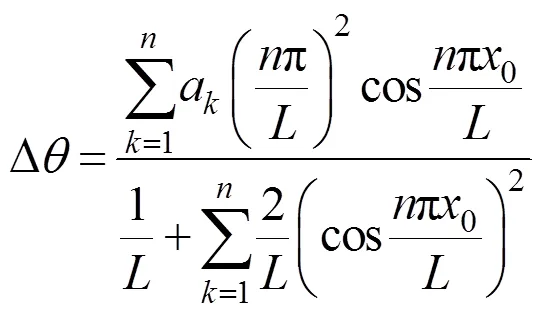
将脱空迭代完成的0~a代入式(26)计算转角的第1次迭代值Δ(1)；将Δ(1)代入式(25)以计算系数并进一步通过式(26)计算转角的第2次迭代值Δ(2)；重复迭代直至前后2次迭代计算的转角符合精度要求为止。

迭代完成后，将系数0~a代入式(10)即可求得轨道变形。轨道结构的实际弯矩(使梁下侧受拉为正)和剪力(使截面右侧梁段产生顺时针转动为正)要去除相当荷载的影响。由弯矩、剪力与竖向位移的微分关系可得如下的计算公式：

4 算例验证和参数分析

用MATLAB编写计算程序，求解方程组(25)采用LU分解法，求解()零点采用牛顿迭代法。傅里叶级数项数取200项，即方程组(25)中=200。

单块浮置板长度为30 m。当浮置板中部位于隧道底板最大变形处时(0=±15 m)，模型取3块浮置板，总长为90 m(=45 m)；当剪力铰位于隧道底板最大变形处时(0=0)，模型取2块浮置板，总长为60 m(=30 m)。

钢轨线密度为60 kg/m，弹性模量为210 GPa，截面惯性矩为3.217×10−5m4；钢弹簧刚度为8 kN/mm，间距为1.2 m；浮置板密度为2 420 kg/m3，弹性模量为30 GPa，宽度为3.3 m，厚度为0.6 m。钢弹簧在隧道底板变形之前已经产生了较大的初始压缩量，为了突出隧道底板变形对轨道变形的影响，在计算所得的轨道变形中去掉轨道的初始位移(根据轨道结构自重求得初始位移为3.570 mm)。

用有限元软件ANSYS建立单层弹性地基梁模型和弹性地基梁-板模型[8](钢轨为梁，浮置板道床为板)，计算参数与理论模型相同。梁采用BEAM4单元划分，单元长度为100 mm。板采用SHELL63单元划分，单元尺寸为300 mm×300 mm。将有限元模型节点的横向自由度约束以减少方程数目。计算结果对比列于表2，轨道变形曲线对比如图3 所示。

表2 不同计算模型的计算结果对比

(a) 工况1；(b) 工况2；(c) 工况3；(d) 工况4

由表2和图3可知，级数法与数值模拟得到的计算结果差别不大，轨道变形曲线基本吻合，证明了本文方法的正确性。与数值模拟相比，级数法的优越性在于：级数法与数值模拟均需要求解线性方程组，级数法的方程组规模远小于数值模拟。以算例中工况2为例，级数法只需求解201个方程，而数值解法中，弹性地基梁模型需要求解的方程个数为901×3+2×1=2 705个，梁−板模型需要求解的方程个数为3 612×2+24×1+2 699=9 947个。

下面将基于本文方法，在上述轨道结构参数基础上，讨论钢弹簧浮置板轨道与隧道底板的相互作用规律。

4.1 隧道底板变形的影响

4.1.1 隧道底板最大变形与剪力铰的位置关系

由表2可见，工况2和4与工况1和3相比，轨道结构变形较小，轨道与隧道底板变形差异较大，脱空范围也较大。说明对于计算脱空来说，浮置板道床中部位于隧道底板最大变形处为不利工况。因此当剪力铰与隧道最大变形位置关系不明确时，可假定浮置板道床中部位于隧道底板最大变形处，以得到脱空范围及脱空量的保守估计。

4.1.2 隧道底板最大变形0

0的取值范围为0~80 mm，沉降槽宽度=3 m，剪力铰位于=±15 m(下同)。0与轨道变形和脱空范围的关系如图4所示。

由图4可见，隧道底板隆起时，轨道变形随隧道隆起量的增大呈线性增长；隧道底板沉降时，轨道变形随隧道沉降量的增大呈逐渐平缓的增长趋势。这是因为浮置板道床具有较大的纵向抗弯刚度，隧道底板沉降时，轨道自身刚度能够避免其产生过大挠度；而隧道底板隆起时，轨道被迫在最大隆起位置产生与隧道底板一致的变形，其挠度与隧道底板沉降时相比大大增加。

轨道与隧道底板的脱空范围随隧道变形的增大而增大。当隧道最大变形量小于20 mm时，隧道沉降引起的脱空范围大于隧道隆起。隧道隆起引起的脱空范围随隧道变形的增大发展较为迅速，当隧道最大隆起量大于40 mm时，脱空范围约为隧道沉降引起脱空范围的2倍。

4.1.3 隧道底板沉降槽宽度

的取值范围为2~5 m，隧道最大变形0=40 mm。与轨道变形和脱空范围的关系如图5所示。

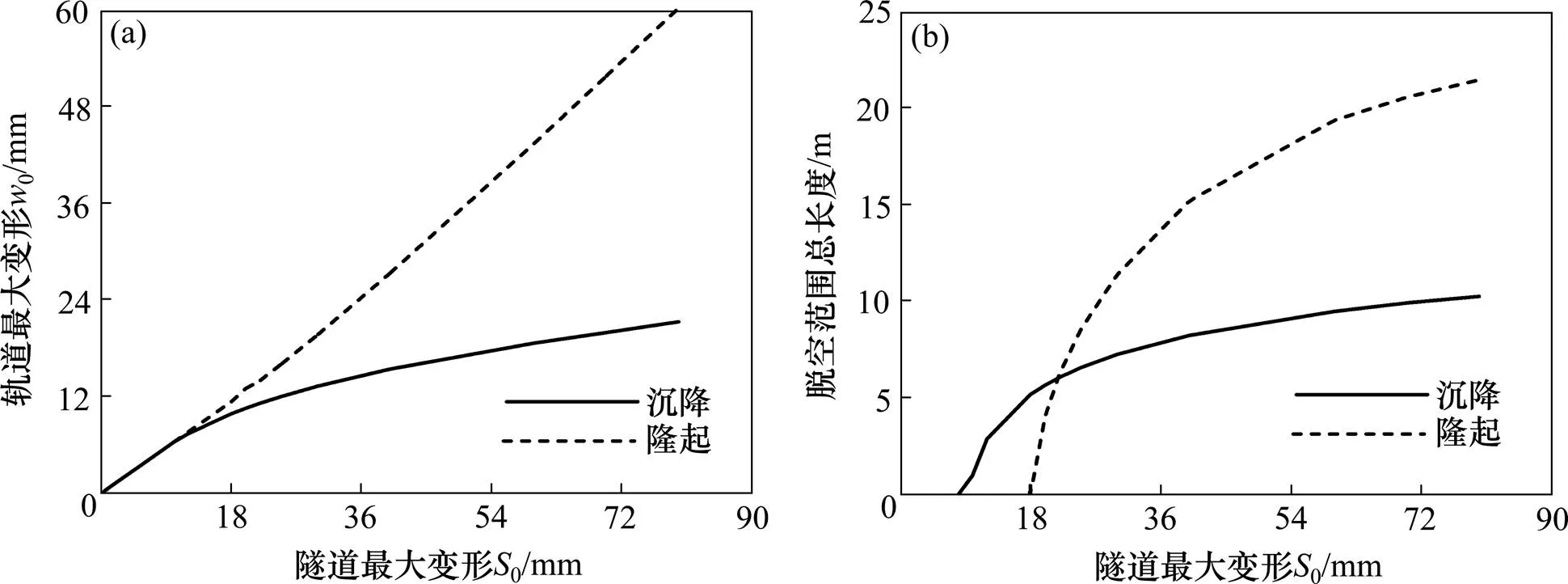
图4 隧道底板最大变形的影响

图5 隧道底板沉降槽宽度的影响

由图5可见，随隧道底板沉降槽宽度的增大，轨道结构最大变形最终与隧道底板最大变形趋同。这是由于沉降槽宽度与隧道纵向变形的不均匀程度有关，越大，隧道底板沉降不均匀性越小，轨道结构与隧道底板之间的变形差异越小。

轨道与隧道底板的脱空范围随隧道底板沉降槽宽度的增大呈先增大后减小的趋势。这是因为较小时，隧道不均匀变形的影响范围较小，此时脱空范围随不均匀变形影响范围的扩大而增大；增大到一定程度之后，轨道与隧道的变形差异逐渐减小，脱空范围也随之减小。

轨道与隧道底板能否产生脱空，与0和2个参数均有关系。轨道与隧道底板恰好产生脱空时的0−组合构成了图6所示的2条曲线。可见，随着值的增大，轨道与隧道底板产生脱空时的0值越来越大，说明随隧道底板沉降槽宽度的增大，轨道与隧道底板的脱空难度增大。值相同的情况下，隧道底板沉降对应的0小于隧道隆起，说明隧道沉降比隆起更容易使轨道与隧道产生脱空。

4.2 钢弹簧刚度及间距的影响

上述讨论中，钢弹簧刚度为8 kN/mm，间距为1.2 m，折合地基系数=4.040 MPa/m。钢弹簧的刚度和间距与式(7)中地基系数的取值有关，为此，取不同的地基系数计算钢弹簧刚度和间距对轨道脱空的影响。值增大，表明钢弹簧的间距减小，或者刚度增大；值减小，表明钢弹簧的间距增大，或者刚度减小。图7为隧道底板沉降时采用不同地基系数计算得到的恰好产生脱空时的0−曲线。图8为轨道与隧道底板脱空范围随值的变化关系，其中0=40 mm，=3m。

图6 S0和i对轨道与隧道底板脱空的影响

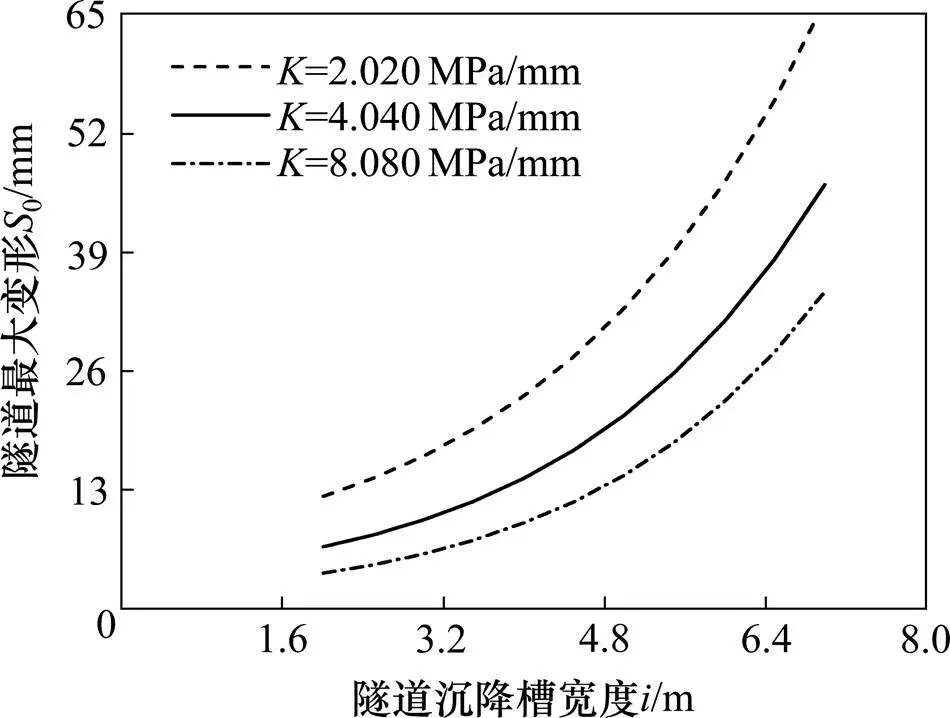
图7 不同地基系数对应的S0−i曲线

由图7及图8可见，值越大，相同沉降槽宽度对应的隧道最大变形0越小，且脱空范围随的增大而增大，说明值越大，轨道与隧道脱空越容易，且脱空范围更大。这是因为钢弹簧竖向刚度增大或者间距减小使得地基系数增大，轨道自重引起的钢弹簧初始压缩量减小，轨道与隧道底板越容易产生脱空，也将产生更大的脱空范围。

图8 地基系数对脱空范围的影响

5 结论

1) 浮置板道床自身有较大抗弯刚度且与基底不是一体，因而变形与基底不同步，当基底变形过大时可与基底产生脱空。可假定浮置板道床中部位于隧道底板变形最大处，以得到脱空范围及脱空量的保守值。

2) 随着隧道底板最大变形0的增大，轨道结构变形和脱空范围均增大；随着沉降槽宽度的增大，轨道结构变形与隧道底板逐渐趋近，脱空范围呈先增大后减小的趋势。

3) 轨道与隧道底板产生脱空是0和2个参数共同影响的结果。随着值的增大，轨道与隧道底板越不容易产生脱空；值相同的情况下，隧道底板沉降比隆起更容易引起轨道与隧道产生脱空。

4) 钢弹簧的竖向刚度和间距影响轨道与隧道底板脱空的难易程度。钢弹簧刚度越大，间距越小，轨道与隧道底板越容易产生脱空，脱空范围越大。

[1] 白海卫, 王剑晨, 刘运亮, 等. 既有地下结构受下穿施工影响的力学响应与安全控制研究[J]. 岩土工程学报, 2019, 41(5): 874−884. BAI Haiwei, WANG Jianchen, LIU Yunliang, et al. Safety control and mechanical response of existing underground structures induced by excavation of new tunnels under construction[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(5): 874−884.

[2] Ng W W, Thayanan B, David M. Three-dimensional centrifuge and numerical modeling of the interaction[J]. Canadian Geotechnical Journal, 2013, 50(9): 935−946.

[3] LIU X, FANG Q, ZHANG D, et al. Behaviour of existing tunnel due to new tunnel construction below[J]. Computers and Geotechnics, 2019(110): 71−81.

[4] LIU X, FANG Q, ZHANG D, et al. Mechanical responses of existing tunnel due to new tunnelling below without clearance[J]. Tunnelling and Underground Space Technology, 2018(80): 44−52.

[5] 姚海波. 大断面隧道浅埋暗挖法下穿既有地铁构筑物施工技术研究[D]. 北京: 北京交通大学, 2005: 145− 148.YAO Haibo. Research on construction technology of large section tunnel crossing under the existing subway tunnel by means of shallow tunneling method[D]. Beijing: Beijing Jiaotong University, 2005: 143−148.

[6] 张群. 路基不均匀沉降对双块式无砟轨道的影响研究[D]. 成都: 西南交通大学, 2007: 40−43.ZHANG Qun. Study of double block ballastless track causing by subgrade differential settlement[D]. Chengdu: Southwest Jiaotong University, 2007: 40−43.

[7] 赵坪锐, 肖杰灵, 刘学毅. 梁端位移对无砟轨道扣件系统的影响分析[J]. 铁道学报, 2008, 30(5): 68−73.ZHAO Pingrui, XIAO Jieling, LIU Xueyi. The influence of the displacement at bridge ends to the fastening systems used on ballastless tracks[J]. Journal of the China Railway Society, 2008, 30(5): 68−73.

[8] 孙璐, 段雨芬, 高培培. 高速铁路板式无砟轨道的结构分析模型对比[J]. 东南大学学报(自然科学版), 2013, 43(5): 938−943.SUN Lu, DUAN Yufen, GAO Peipei. Comparison of structural analysis models for slab ballastless track in high-speed railway[J]. Journal of Southeast University (Natural Science Edition), 2013, 43(5): 938−943.

[9] 程霖, 杨成永, 李延川, 等. 带接头地下管线变形的傅里叶级数解[J].湖南大学学报(自然科学版), 2018, 45(11): 149−156. CHENG Lin, YANG Chengyong, LI Yanchuan, et al. Fourier series solution for deformation of buried jointed pipelines[J]. Journal of Hunan University (Natural Sciences), 2018, 45(11): 149−156.

[10] 杨建近, 朱胜阳, 翟婉明. 浮置板剪力铰对列车-轨道耦合系统动力学行为的影响[J]. 振动与冲击, 2019, 38(11): 1−8. YANG Jianjin, ZHU Shengyang, ZHAI Wanming. Effects of shear hinges of floating slab on dynamic behavior of a train-track coupled system[J]. Journal of Vibration and Shock, 2019, 38(11): 1−8.

[11] 杨成永, 程霖, 余乐, 等. 隧道沉降引起的轨道结构变形与脱空[J]. 中国铁道科学, 2018, 39(6): 37−43. YANG Chengyong, CHENG Lin, YU Le, et al. Deformation and cavity of track structure due to tunnel settlement[J]. China Railway Science, 2018, 39(6): 37− 43.

[12] 杨成永, 程霖, 李延川, 等. 隧道结构隆起引起的轨道结构变形与脱空[J]. 铁道工程学报, 2019, 36(3): 19−25, 77. YANG Chengyong, CHENG Lin, LI Yanchuan, et al. Deformation and detachment of track structures induced by upheaval of tunnel structure[J]. Journal of Railway Engineering Society, 2019, 36(3): 19−25, 77.

[13] Attewell P B, Yeats J, Selby A R. Soil movements induced by tunneling and their effects on pipelines and structures[M]. London: Blackie and Son Ltd, 1986: 53− 60.

Analysis on deformation and detachment of the steel spring floating slab track induced by tunnel deformation

CHENG Lin1, YANG Chengyong1, MA Wenhui1, CHE Jingke2

(1. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China; 2. Beijing General Municipal Engineering Design & Research Institute Co., Ltd, Beijing 100082, China)

Traversing construction induces deformation of the existing tunnel and track structures within, which has side-effects on operation safety of trains. The steel spring floating slab track was simplified as a beam on elastic foundation. A governing differential equation for deformation of track structures was established and solved by Fourier series method. A set of linear equations for determining unknown series coefficients was obtained. An iterative method to solve the set of equations was given. Based on the method presented in this paper, interaction between steel spring floating slab track and tunnel floor was analyzed. Results show that, the flexural stiffness of floating slab causes differential deformation, or further detachment, between track slabs and the tunnel floor. The deformation of track structures and the detachment range increase with the increase of tunnel floor deformation. With the increase of width of settlement trough, the deformation of track and tunnel floor approaches gradually, and the detachment range first increases and then decreases. The greater the stiffness of steel springs or the smaller the spacing between two adjacent springs, the more likely the track separates from the tunnel floor, and the wider the detachment range will be. The research results provide theoretical guidance for safety evaluation of the existing track structures during traversing construction.

traversing construction; steel spring floating slab track; deformation; detachment; Fourier series solution

TU91

A

1672 − 7029(2020)04 − 0849 − 09

10.19713/j.cnki.43−1423/u.T20190616

2019−07−09

中央高校基本科研业务费专项资金资助项目(2018YJS119)；国家自然科学基金资助项目(51478032)

程霖(1992−)，男，山东聊城人，博士研究生，从事隧道与地下工程研究；E−mail：bjd_chenglin@163.com

(编辑 涂鹏)