基于PCA-改进TOPSIS的铁路桥梁加固改造方案决策

裴兴旺，李慧民，李轩，李文龙，黄俊杰

基于PCA-改进TOPSIS的铁路桥梁加固改造方案决策

裴兴旺1，李慧民1，李轩2，李文龙1，黄俊杰3

(1. 西安建筑科技大学 土木工程学院，陕西 西安 710055；2. 陕西通宇公路研究所有限公司，陕西 西安 710118；3. 中冶建筑研究总院有限公司，北京 100088)

为降低我国铁路桥梁加固改造过程中存在的潜在风险，并考虑现有决策方法存在的不足，依据问题特点建立科学的决策指标体系，提出一种基于主成分分析法(PCA)和加权广义马氏距离改进TOPSIS的决策模型。首先，利用三角模糊数等方法对指标进行量化与熵权赋值，采用主成分分析法按累计方差贡献率实现指标的降维处理；其次，依据加权广义马氏距离改进TOPSIS方法计算各指标方案与正负理想解的距离并进行方案排序；最后，以5例工程实例验证本文方法的可信性和优越性，所选方案能最大限度地实现性能提升、经济合理等要求。

铁路桥梁；加固改造；方案决策；主成分分析；改进TOPSIS

我国铁路桥梁加固改造是社会化进程中的重要策略，是可持续发展战略在交通运输领域的体现和升华。铁路桥梁加固改造有别于新建项目[1]，加固改造设计方案需要最大程度地发挥原结构的利用价值，实现性能提升、经济合理和技术可行等要求。加固改造方案涉及加固改造方法的选择、新旧结构体系协同工作和承载能力验算等关键环节，并存在因设计人员对原结构体系理解失误、相关工程经验不足和计算模型可信度低等原因导致的潜在风险。此外，桥梁多位于自然环境宜人的大江大河和自然保护区，这需要对受损构件进行加固设计和利用原桥梁结构体系进行改造设计的同时，妥善处理诸如加固改造材料盲目选择造成的环境破坏、野蛮施工超挖超建导致的植被覆盖及水土流失等诸多不确定环境因素。近年来，国内外相关学者在桥梁加固改造方案决策方面进行了诸多研究，Ellakwa等[2]对纤维增强复合材料不同布置方法及位置对桥梁加固效果的影响进行了分析。Hassan等[3]对碳纤维布(CFRP)整体加固和玻璃纤维布(GFRP)钢筋复合加固两种不同加固方案的性能进行了对比分析。张鹏[4]采用层次分析法对桥梁加固方案开展了优选研究；杨雅勋等[5]采用基于改进AHP法和熵值法的组合权值法结合灰关联法展开对旧桥加固方案的评价研究；边晶梅等[6]建立了服役桥梁加固方案优选决策支持系统，姜禹等[7]基于熵值-关联度法展开桥梁加固方案优选模型的研究。周长东等[8]基于层次分析法的模糊决策理论展开对震后桥梁结构应急加固方案优选模型的研究。常见的决策方法有灰色支持向量机法(SVM)、证据推理法(D-S)和逼近理想解法(TOPSIS)等，这其中因TOPSIS理论成熟，计算方法简单，应用过程直观而被学者们广泛应用[9−10]。过往研究取得了一定成果但仍存在如下不足：1) 指标体系建立未考虑各指标之间的内部联系，且指标数据样本过大，相互之间存在较强的关联性，直接分析易导致数据失真；2) 研究方法比较单一，容易产生同时逼近正负理想解、无法同时解决协方差矩阵为0或不可逆时计算不能进行、数据量过大导致数据灾难等缺陷。3) 研究内容主要集中在单一桥梁构件加固等方面，涉及到铁路桥梁整体加固改造的研究不充分。鉴于此，本文拟利用三角模糊数等方法对指标进行量化及熵权赋值，采用主成分分析法按方差贡献率实现数据降维，待数据处理后引入加权广式马氏距离改进TOPSIS法，计算方案的相对贴近度，结合实例对备选方案进行优劣排序，加以验证。

1 理论基础

1.1 主成分分析法

主成分分析(Principal Component Analysis)[11]是一种建立在统计最优原则基础上的特征选取分析方法，最早由Pearson于1901年首次提出；基本理念是在尽可能多地保留数据集中方差的同时，减少该数据集的维度，计算特点是内部模型为线性的，完全不受参数限制，具体步骤如下。

Step 1：首先对方案决策指标进行筛选，对于个样本维特征变量构建指标体系数据矩阵，对矩阵中各指标元素进行规范化处理。

Step 2：求规范化后矩阵*的样本相关系数矩阵：

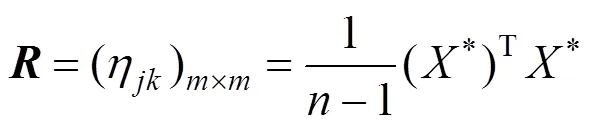
其中：=1, 2, …,,=1, 2, …,，为指标与指标的相关系数。

即可得综合评价函数：

Step 5：基于主成分分析，根据综合评价函数值对各方案进行排序。

1.2 加权广义马氏距离法

1.2.1 广义马氏距离

马氏距离是由印度学者Mahalanobis于1936年提出的一种统计距离。将马氏距离代替欧氏距离应用于TOPSIS方法中能有效解决指标间的相关性问题，计算公式如下：

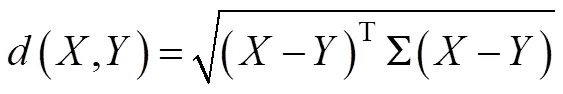
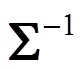
1.2.2 加权广义马氏距离

广义马氏距离考虑了指标之间的相关性，消除了指标量纲的影响，解决了协方差矩阵不可逆的问题，但没有考虑到指标间的重要性差异，而用加权广义马氏距离代替欧氏距离应用于TOPSIS方法中将有效解决指标间的重要性差异、不同量纲和相关性对决策结果的影响以及协方差矩阵不可逆的问题[12]，计算公式如下：

1.2.3 基于加权广义马氏距离改进TOPSIS法

改进TOPSIS法有效解决了指标间的重要性差异、不同量纲和相关性对决策结果的影响以及协方差矩阵不可逆的问题，具体步骤如下。

Step 1：构造包含个备选方案个指标的原始决策矩阵。

Step 2：确定正负理想解+和−。

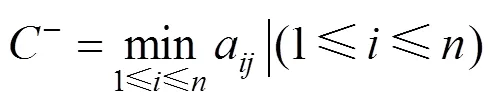
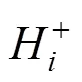
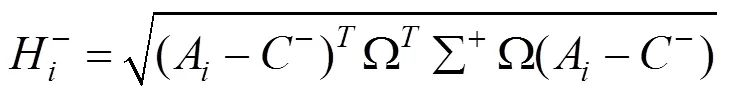
Step 4：计算各方案相对理想解的贴近度。

Step 5：各方案排序，贴近度越大方案越优。

2 铁路桥梁加固改造方案决策模型构建

2.1 决策指标体系构建

本文铁路桥梁加固改造方案决策指标体系的构建，依据指标构建的基本原则，在多次调研和查阅相关文献的基础上[2−3, 8]，对影响方案决策的相关因素进行总结，实现指标体系的阶梯层次性，最终建立了铁路桥梁加固改造方案决策指标体系，如图1所示。

1) 性能提升Q1：性能提升是铁路桥梁加固改造项目的初衷，桥梁技术状况等级、桥梁承载能力和桥梁耐久性能这3项指标是性能提升的关键，直接决定着铁路桥梁加固改造项目的成败。

2) 经济合理Q2：经济合理是方案选择的关键因素，对于铁路桥梁加固改造项目来说，不仅要需要考虑工期、造价及原结构利用率等直接因素，同时需考虑中断交通损失及后续使用年限和后续维护成本等间接因素。

3) 技术可行Q3：技术可行是保障铁路桥梁加固改造项目顺利进行的关键。首先要考虑加固改造技术的成熟度、大型机械的依赖程度及构造措施的合理程度；其次要考虑加固材料的供应难度和现场环境的制约情况；最后要考虑新旧结构的协同工作及现有方案对原桥梁的扰动程度。

4) 社会影响Q4：社会影响是评判基础设施建设项目成功与否的重要指标。铁路桥梁为区域经济和社会发展做出了重要贡献，是经济实力和文化自信的重要体现。加固改造方案的选择要综合考虑铁路桥梁加固改造后对交通功能、社会舆论、使用功能及桥梁外观等方面的影响。

5) 生态安全Q5：树立和践行绿水青山就是金山银山的理念，是指引建设美丽中国的理论明灯，建设生态文明是中华民族永续发展的千年大计，铁路桥梁多位于自然环境宜人的大江大河和自然保护区，因此，进行方案决策时需考虑到加固改造方案对区域生态环境的不良影响。

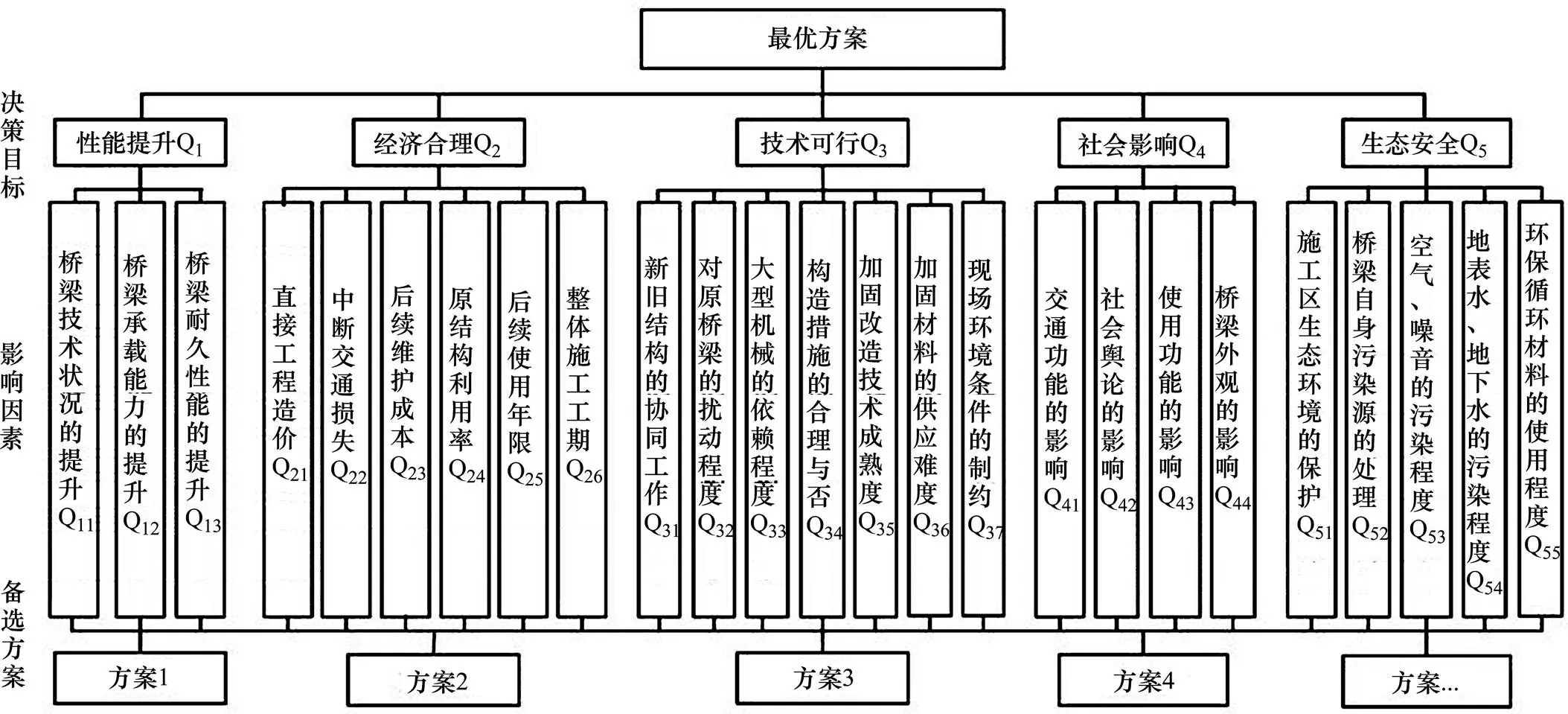
图1 铁路桥梁加固改造方案决策指标体系

2.2 决策模型计算过程

Step 1：在铁路桥梁加固改造方案决策问题中，假定有个备选方案，由专家组对个方案中的个指标数据进行提取(定量指标数据从方案中直接提取，定性指标数据采用语言模糊数法进行提取)，核定后得数据矩阵。

Step 2：对个备选方案首先进行“加固改造价值”评价，当铁路桥梁加固改造成本比拆除新建节省费用 60%以上认为是有价值的，符合要求则进行下一步计算，不符合则判为最差方案。

Step 3：本文所建立的铁路桥梁加固改造方案决策指标体系由定量和定性指标组成，且分为效益型指标1和成本型指标22种，计算之前需先进行规范化处理[13]。数据矩阵采用三角模糊数等方法进行规范化处理，得规范化矩阵*，结合熵权 法[14]计算各指标权重。

1) 定性指标按下式计算：

定性指标采用三角模糊数[15]进行量化。记为语义状态集，{,,,,,,}，依次对应着7个状态“特别差~特别好”。将转换为三角模糊数，见表1。

表1 语言类模糊数与三角模糊数的相互转换

效益型和成本型指标规范化计算公式如下：

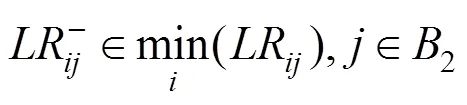
为简便运算，将三角模糊数转化为精确数，计算公式如下：

2) 定量指标按下式计算：

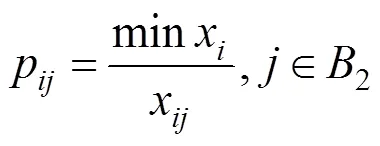
待定量、定性指标经规范化处理后进行归一化处理，计算公式如下：

Step 5：经主成分分析后，得旋转矩阵T，将T按式(2)~(3)计算得到矩阵，即降维后的基于主成分分析的各方案决策矩阵。

Step 6：将矩阵结合加权广义马氏距离改进的TOPSIS方法进行铁路桥梁加固改造方案排序。

3 实例分析

3.1 项目概况

从作者实际参与的诸多桥梁加固改造项目中选取5个具有代表性的项目为研究样本：XPT桥、WF桥、TFG桥、UW桥和HDH桥，检验所建模型的可信性与有效性，部分案例汇总于专著《土木工程安全检测、鉴定、加固修复案例分析》中，这里以XPT桥为例详细阐述计算过程。该桥建于1997年，全长3 245 m，预应力混凝土简支箱梁。经检测，该桥承载能力严重不足，考虑到该桥区域位置的重要性，特进行加固改造。

3.2 计算过程

XPT铁路桥梁加固改造项目由2家甲级设计院合计提出了5种加固改造设计方案，即方案A1~A5。在方案决策之初，首先对提出的5种方案进行“改造价值评价”，所有方案均通过专家组论证，随即从方案A1~A5中按三角模糊数转化得到各指标的量化值，见表2。

3.2.1 指标权重计算

按式(11)~(16)对表2中的数据进行规范化处理，得规范化矩阵*，见矩阵(18)。

熵权法计算各指标权重，得=(0.010 4，0.003 2，0.007 4，0.057 0，0.170 3，0.015 8，0.000 4，0.005 0，0.010 7，0.033 2，0.065 7，0.068 7，0.010 4，0.006 1，0.018 0，0.018 0，0.068 7，0.068 7，0.065 7，0.011 2，0.043 9，0.033 2，0.086 8，0.086 8，0.013 7)。

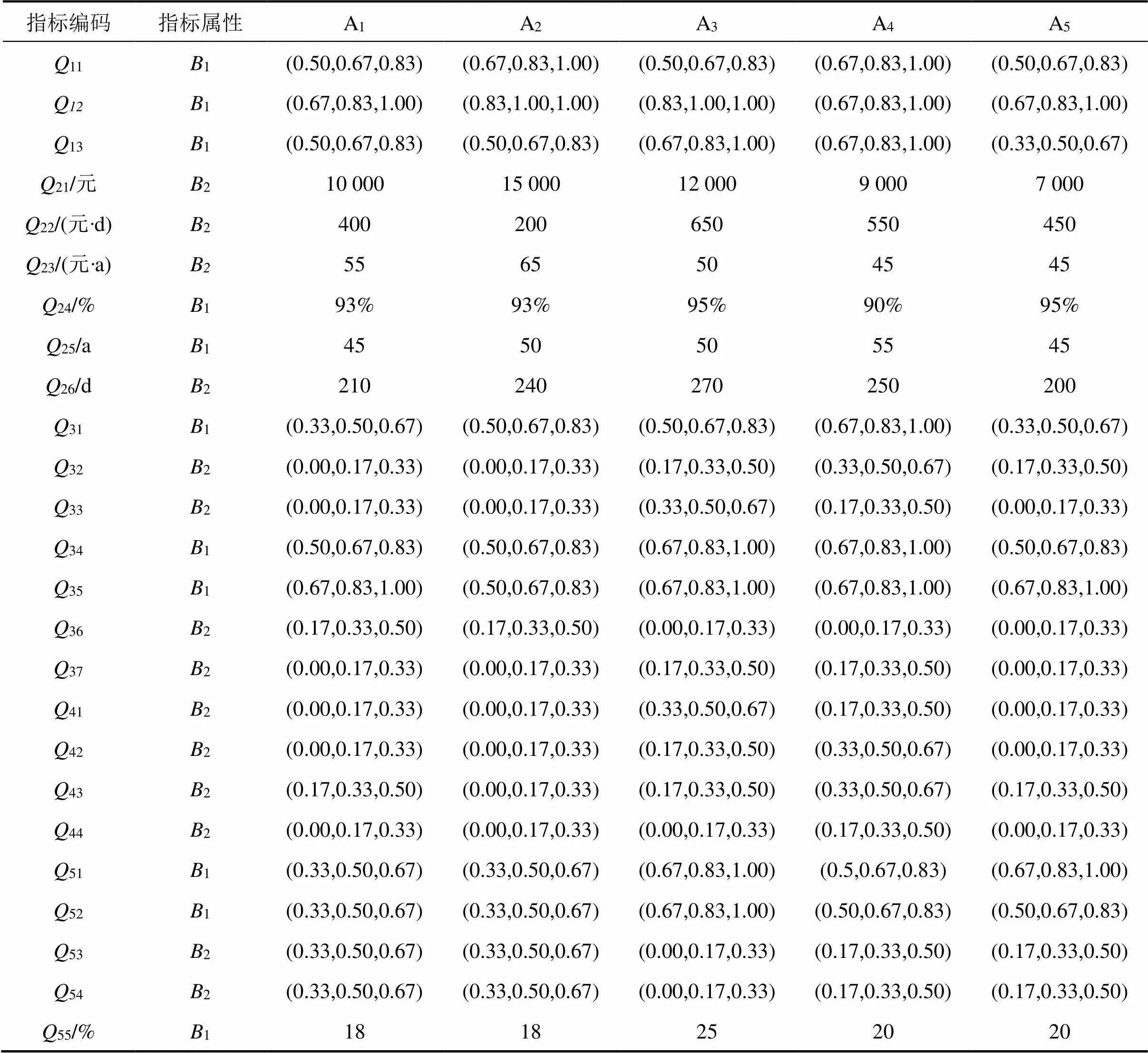
表2 初始决策指标量化值

3.2.2 主成分分析降维

采用spss24.0软件对25个指标进行主成分分析，得到各项指标的相关系数矩阵(篇幅有限，不再给出)，从中可知，11，26，31和34等指标具有较高的正负相关性。计算各指标的初始特征值及累计方差百分比，前3个主成分1，2和3的累计方差百分比大于85%，主成分碎石图如图2所示，特征值和方差贡献率见表3。

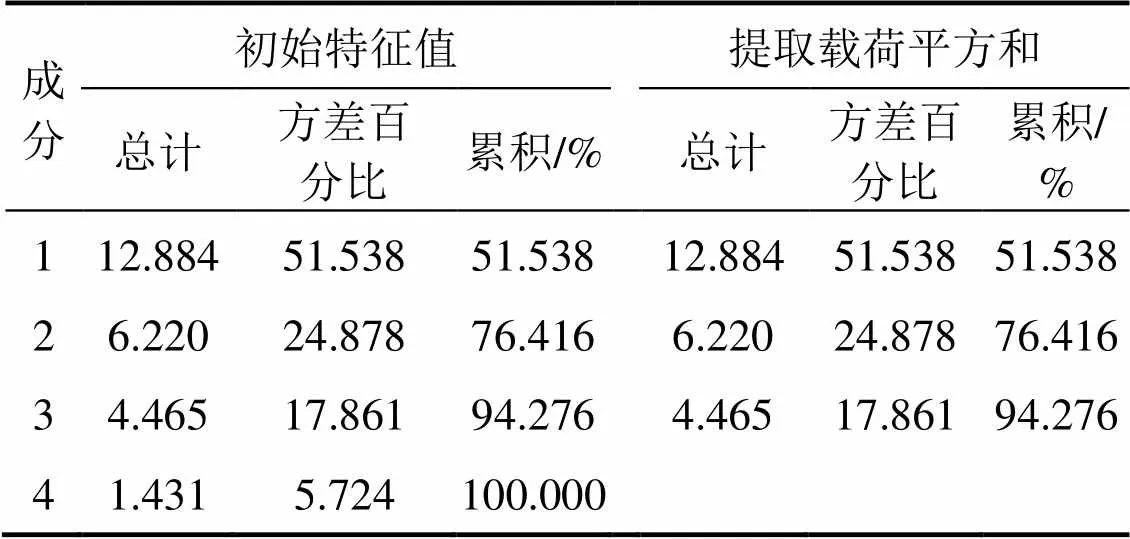
表3 特征值和方差贡献率

图2 主成分碎石图

表4 旋转矩阵(XT)

由spss24.0软件提取主成分初始负载矩阵，旋转得矩阵T，见表4。从旋转矩阵T可以看出，主成分1与指标13，23，25，31，34，35，36，51，52，53，54和55；主成分2与指标21，24和26；主成分3与指标12和44，关联性较大，由此可得主成分1，2和3的权重分别为：0.830，0.099和0.071。从图2及表3中可以看出，主成分中前3项因子成分的特征根的累计方差贡献率达到94.276%，因此，从图2中选取前3个因子作为主成分因子，进行数据分析。

根据上述矩阵所列的主成分指标权重，按照式(3)，即可得到3个主成分表达式：

计算各方案主成分得分，将方案得分代入上面3个表达式，得到5个方案的相应主成分得分，并乘以各主成分指标对应的权重，结果见表5。

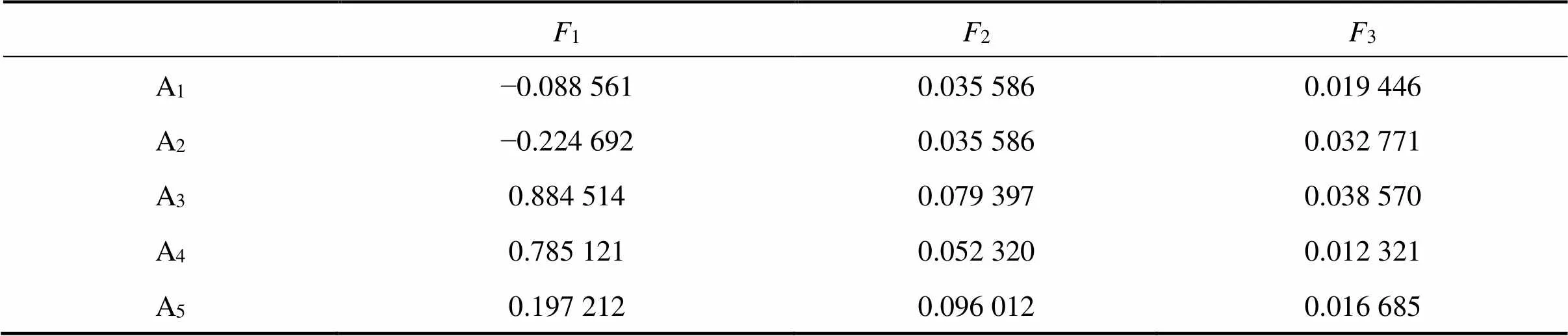
表5 基于主成分各方案决策得分Fi

3.2.3 加权广义马氏距离求解

表6 加权广义马氏距离、贴近度

3.3 结果分析

主成分分析按累计方差贡献率实现了指标的降维处理，避免因样本过大、关联性较强导致的数据失真、排序不可信的问题，体现了主成分分析法在方案决策过程中的优越性。为了便于比较，将本文提出的方法与PCA+其他TOPSIS方法对比分析(欧式距离P1，马式距离P2，广义马式距离P3和本文方法P4)，得贴进度及排序结果，见表7。结果表明，传统方法与本文方法的排序在最优方案上保持一致，均为3，验证了本文方法的可信性。但其他方案排序不尽相同，其中，本文提出的方法(P4)与方法(P3)存在方案A2，A4和A5排序不一致的情况；与方法(P2和P1)存在方案A1和A2排序不一致的情况，这是因为本文所提出的方法在计算过程中考虑了指标之间的重要性关系，解决了指标之间因重要性差异导致计算结果不科学的问题；此外，本文提出的方法可以同时解决当协方差矩阵为0或不可逆时计算无法进行的问题，使得分析结果更加可信。

表7 不同方法计算结果：贴进度、排序

同理，对WF桥、TFG桥、UW桥和HDH桥加固改造项目的决策过程按本文提出的方法进行计算，结果见表8。

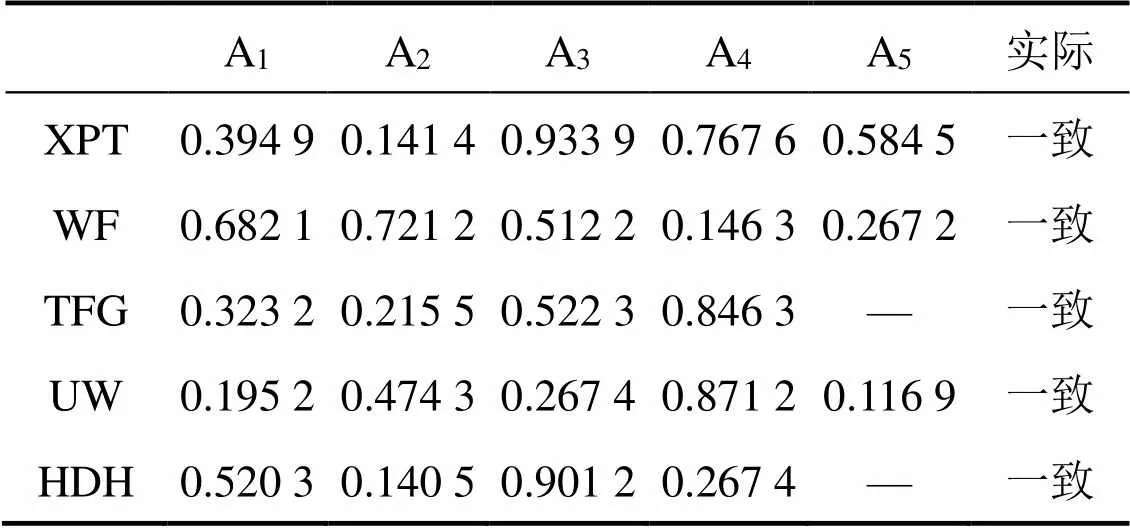
表8 其余项目计算结果：贴进度、实际情况对比

从表8中可知，WF铁路桥最优方案为A2，TFG铁路桥最优方案为A4，UW铁路桥最优方案为A4，UW铁路桥最优方案为A3。通过对项目实地情况的调查情况可知，实际情况与模型决策的排序结果均保持一致，相比于传统决策方法，本文所建立的方法降低了决策过程的复杂性，提高了决策过程的可靠性，所选方案能够最大限度的实现性能提升、经济合理、技术可行、社会影响、生态安全的要求，对类似项目决策具有良好的指导作用。从而验证了所建模型的可信性和有效性。

4 结论

1) 通过实例调研和文献分析，对铁路桥梁加固改造项目决策影响因素进行分析识别，建立包括性能提升、经济合理、技术可行、社会影响和生态安全5个方面在内的铁路桥梁加固改造项目决策指标体系。

2) 运用三角模糊数对指标进行量化与熵权赋值，降低了人为因素的主观性；采用主成分分析法按累计方差贡献率实现指标的降维处理，降低决策过程的复杂性，提高铁路桥梁加固改造方案决策的可靠性。

3) 构建基于PCA改进TOPSIS的铁路桥梁加固改造方案决策模型，并运用于工程实例中。结果表明，决策过程清晰，决策结果可靠，同时解决了当协方差矩阵为0或不可逆时计算无法进行、指标之间存在重要性差异致使计算结果不科学、数据量过大导致数据灾难这3点缺陷，使得改进后的方法更加全面合理，为类似项目决策提供指导。

[1] 马建, 孙守增, 杨琦, 等. 中国桥梁工程学术研究综述2014[J]. 中国公路学报, 2014, 27(5): 1−96. MA Jian, SUN Shouzeng, YANG Qi, et al. Review on China’s bridge engineering research: 2014[J]. China Journal of Highway and Transport, 2014, 27(5): 1−96.

[2] Ellakwa A E, Shortall A C, Shehata M K, et al. The influence of fibre placement and position on the efficiency of reinforcement of fibre reinforced composite bridgework[J]. Journal of Oral Rehabilitation, 2010, 28(8): 785−791.

[3] Hassan T, Abdelrahman A, Tadros G, et al. Fibre reinforced polymer reinforcing bars for bridge decks[J]. Canadian Journal of Civil Engineering, 2000, 27(5): 839− 849.

[4] 张鹏. 桥梁加固方案的层次分析优选法[J]. 公路交通科技, 2006, 23(7): 92−95. ZHANG Peng. Choice of optimum scheme for bridge strengthening by using analytic hierarchy process[J]. Journal of Highway and Transportation Research and Development, 2006, 23(7): 92−95.

[5] 杨雅勋, 李子春, 李子青. 基于组合权值灰关联法的旧桥加固方案评价[J]. 长安大学学报(自然科学版), 2007, 27(5): 62−65. YANG Yaxun, LI Zichun, LI Ziqing. Evaluation on reinforcement scheme of existing bridges based on combination-weight-gray-relation method[J]. Journal of Chang’an University (Natural Science Edition), 2007, 27(5): 62−65.

[6] 边晶梅, 朱浮声, 高晓刚, 等. 服役桥梁加固方案优选决策支持系统[J]. 中外公路, 2009, 29(2): 156−161. BIAN Jingmei, ZHU Fusheng, GAO Xiaogang, et al. Decision support system for optimum selection of reinforcement scheme of service bridges[J]. Journal of China and Foreign Highway, 2009, 29(2): 156−161.

[7] 姜禹, 郝伟. 基于赋权关联度法的桥梁加固方案优选研究[J]. 铁道科学与工程学报, 2016, 13(7): 1318− 1322. JIANG Yu, HAO Wei. Research on bridge reinforcement scheme optimization based on empowerment relational degree[J]. Journal of Railway Science and Engineering, 2016, 13(7): 1318−1322.

[8] 周长东, 白晓彬, 张艾荣, 等. 震后桥梁结构应急加固方案优选[J]. 工程抗震与加固改造, 2011, 33(3): 82−87. ZHOU Changdong, BAI Xiaobin, ZHANG Airong, et al. Emergency strengthening scheme optimization for post-earthquake bride structure[J]. Earthquake Resistant Engineering and Retrofitting, 2011, 33(3): 82−87.

[9] ZHANG J, Iwaasa A D, HAN G, et al. Utilizing a multi-index decision analysis method to overall assess forage yield and quality of C3 grasses in the western Canadian prairies[J]. Field Crops Research, 2018, 2(22): 12−25.

[10] 许静, 何桢, 袁荣, 等. 基于主成分分析与TOPSIS模型相结合的函数型产品质量特性的优化方法研究[J].工业工程与管理, 2016, 21(3): 59−67. XU Jing, HE Zhen, YUAN Rong, et al. Optimization of functional product quality characteristic problems based on PAC and TOPSIS model[J]. Industrial Engineering and Management, 2016, 21(3): 59−67.

[11] Grbovic M, LI W C, XU P, et al. Decentralized fault detection and diagnosis via sparse PCA based decomposition and Maximum Entropy decision fusion[J]. Journal of Process Control, 2012, 22(4): 738−750.

[12] 关宏艳, 李宗坤, 葛巍, 等. 基于加权广义马氏距离的TOPSIS方法在水库防洪调度决策中的应用[J]. 天津大学学报(自然科学与工程技术版), 2016, 49(12): 1276− 1281. GUAN Hongyan, LI Zongkun, GE Wei, et al. TOPSIS method based on weighted generalized mahalanobis distance: An application to reservoir flood control operation[J]. Journal of Tianjin University (Science and Technology), 2016, 49(12): 1276−1281.

[13] LI D F. A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems[J]. Computers and Mathematics with Applications, 2010, 60(6): 1557−1570.

[14] HE Y H, GUO H W, JIN M Z, et al. A linguistic entropy weight method and its application in linguistic multi-attribute group decision making[J]. Nonlinear Dynamics, 2016, 84(1): 399−404.

[15] 廖勇. 基于三角模糊数的铁路客运站选址方案评价方法[J]. 中国铁道科学, 2009, 30(6): 119−125. LIAO Yong. Evaluation method for the location selection of railway passenger station based on triangular fuzzy number[J]. China Railway Science, 2009, 30(6): 119− 125.

Decision-making of railway bridge reinforcement and reconstruction scheme based on PCA and improved TOPSIS

PEI Xingwang1, LI Huimin1, LI Xuan2, LI Wenlong1, HUANG Junjie3

(1. College of Civil Engineering, Xi’an University of Architecture & Technology, Xi’an 710055, China;2. Shaanxi Tongyu Highway Research Institute Ltd, Xi’an 710118, China;3. Central Research Institute of Building and Construction Co., Ltd, Beijing 100088, China)

In order to reduce the potential risks in the reinforcement and reconstruction process of railway bridges in China, and considering the shortcomings of the existing decision-making methods, this paper established a scientific decision index system according to the characteristics of the problem, and proposed a decision-making model based on principal component analysis (PCA) and improved TOPSIS method of weighted generalized Mahalanobis distance. Firstly, the triangular fuzzy function is used to quantify the qualitative indexes, then the weight of each index is calculated by the entropy weight method. And using the PCA method to reduce the index dimension according to the contribution rate of the cumulative variance of the index. Secondly, using the improved TOPSIS method of weighted generalized Mahalanobis distance to calculate the distance between each index scheme and the positive and negative ideal solutions. Finally, five engineering examples are given to verify the credibility and superiority of this method. The selected scheme can meet the requirements of performance improvement and economic rationality to the greatest extent.

railway bridge; reinforcement and reconstruction; scheme decision-making; principal component analysis; improved TOPSIS

U24

A

1672 − 7029(2020)04 − 0823 − 09

10.19713/j.cnki.43−1423/u.T20190495

2019−06−04

国家自然科学基金资助项目(51478384，51808424)；住建部科技资助项目(2018-R1-009)

裴兴旺(1988−)，男，河南漯河人，博士研究生，从事土木工程结构安全检测、鉴定、加固修复，土木工程建造与管理研究；E−mail：knowledge1020@126.com

(编辑 阳丽霞)