考虑施工阶段的高铁系杆拱桥吊杆张拉优化研究

王祥国，邓博，杨孟刚

考虑施工阶段的高铁系杆拱桥吊杆张拉优化研究

王祥国1，邓博2，杨孟刚2

(1. 中建铁路投资建设集团有限公司，北京 100053；2. 中南大学 土木工程学院，湖南 长沙 410075)

将影响矩阵法引入系杆拱桥，建立以优化前后吊杆成桥索力差值向量二范数平方的最小值为目标函数，以吊杆张拉力为变量，以各个施工及成桥阶段中系梁和拱肋的挠度、应力以及吊杆索力作为约束条件的优化模型，通过该优化模型的计算来减少施工阶段的吊杆张拉次数。基于该优化模型，以新建某高铁线144 m下承式尼尔森体系简支拱桥为工程实例，获得施工阶段1次张拉的吊杆张拉力。研究结果表明：优化后采用吊杆1次张拉方案的系梁和拱肋的挠度、内力与设计状态较接近，验证了该优化模型的可靠性和有效性。该优化方法可为同类型桥梁的设计和施工提供参考。

系杆拱桥；吊杆张拉；优化模型；施工阶段；影响矩阵

近年来，钢管混凝土系杆拱桥已成为60~200 m跨径范围内非常具有竞争力的桥型之一[1]。简支−梁拱组合体系的系杆拱桥，使梁、拱在受力方面的优点得以充分发挥，因其结构轻巧、外部静定、无水平推力，尤其适合于在河岸淤积层的软弱地基上使用[2−3]。尼尔森体系钢管混凝土拱桥跨越能力强、经济效益好、动力性能优、桥式结构美观，能提供较大的纵向刚度，同时能有效减小振动冲击带来的动力响应等问题，具有良好的安全、平稳、舒适的性能，相较于其他桥型有着明显的优势，从而在高速铁路中得以广泛应用[4-5]。为了使拱和梁的变形更加协调、受力更加均衡，一般设计对吊杆进行2次甚至多批次张拉。但在张拉过程中，每根吊杆的张拉都会对其他已张拉吊杆产生影响，吊杆的多次张拉更会使这些影响变得复杂[6-7]。同时，多次张拉无疑会增加施工成本和工期，加大施工的繁琐性，给施工方带来困扰。因此，在满足规范要求的前提下尽量减少吊杆张拉的次数，对节省施工成本、满足施工进度要求和降低施工难度等有重要意义。目前，已有较多学者引入优化方法对斜拉桥、悬索桥和拱桥的成桥索力进行优化[8-12]。王学明 等[13]在斜拉桥索力影响矩阵的基础上，以结构应变能最小为目标函数，建立了矮塔斜拉桥索力优化模型。GAO等[14]提出了一种多参数混合优化方法，即以全桥混凝土、拉索及预应力束总造价为目标函数，以梁高、拉索面积、拉索恒载索力、梁截面所配预应力为设计变量，以各项规范要求检算指标为约束条件建立优化设计模型。李小年[15]提出了自锚式悬索桥合理成桥状态的分步确定方法。杨俊[16]提出了基于影响矩阵的综合刚性吊杆法和自动调索法来确定系杆拱桥的合理成桥吊杆索力。以上研究能较好地对成桥索力进行优化，使得成桥状态或总体投资达到更优，但对施工时吊索张拉次数和各个施工阶段的应力和挠度都没有做太多的考虑，且均未考虑施工阶段的张拉次数。为了简化系杆拱桥吊杆张拉的施工工序，本文引入影响矩阵法，建立吊杆张拉优化模型，以吊杆张拉次数最少为优化目标。在吊杆张拉优化模型中，以优化前后吊杆成桥索力差值列阵二范数平方的最小值为目标函数，以吊杆张拉力为变量，以各个施工阶段和成桥阶段中系梁和拱肋的内力、位移、应力以及吊杆索力满足规范要求为约束条件。通过优化模型，得到优化后的吊杆张拉力，使得优化后吊杆的成桥索力和设计成桥索力相接近，达到在不改变成桥索力的基础上，减少吊杆张拉次数、节省施工成本、简化施工过程和缩短施工工期的目的。最后，以新建某高铁线144 m下承式尼尔森体系简支拱为工程实例，建立吊杆张拉优化模型，获得基于施工阶段优化后的吊杆张拉索力，验证优化模型的有效性和可靠性。

1 优化模型的建立

1.1 吊杆索力优化的影响矩阵法

由于施工方法的不同，系杆拱桥施工索力的优化相比于斜拉桥而言，混凝土徐变效应的影响较小，因此可采用影响矩阵法对系杆拱桥的吊杆张拉力进行优化，误差较小。影响矩阵主要由受调向量、施调向量和影响向量三者构成。

1) 受调向量：结构中控制截面上的个指定接受调整的独立元素所构成的列向量，并且在整个调值的过程中接受结构调整而达到某种期望， 记为：

式中：y表示控制截面上指定的内力、应力和位移等调整量。

2) 施调向量：结构中可以实施调整从而改变受调向量的个独立元素所构成的列向量，本文中施调向量元素为吊杆张拉力，记为：

3) 影响向量：施调向量中第个元素发生单位变化时，所引起对应受调向量的变化值，记为：

当个施调向量分别发生单位变化时，将得到的个影响向量用矩阵的形式表示出来，即影响矩阵，记为：

当结构体系满足线性叠加原理时，有：

=(5)

在进行拱桥吊杆索力优化的过程中，以各个施工阶段的吊杆张拉力作为施调向量，选取相应施工阶段系梁和拱肋控制截面的挠度和应力作为受调向量。设为吊杆张拉力列阵，为吊杆索力列阵，表示系梁、拱肋控制截面的挠度列阵，c和t分别表示系梁、拱肋控制截面的压应力列阵和拉应力列阵，可以得到：

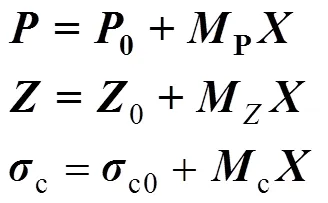
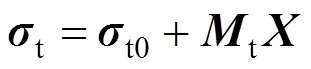
式中：0和0分别为张拉吊杆前的吊杆索力列阵、系梁和拱肋控制截面的挠度列阵，如果是单次张拉，0则为0；c0和t0分别为张拉吊杆施工荷载作用下系梁、拱肋控制截面的压应力列阵和拉应力列阵；P和Z分别为考虑施工顺序下的吊杆索力、系梁和拱肋控制截面挠度对于吊杆张拉力的影响矩阵；c和t分别为考虑施工顺序下的系梁、拱肋控制截面的压应力和拉应力对于吊杆张拉力的影响矩阵。

1.2 优化目标函数

本文的目的是将施工过程中吊杆的2次张拉优化至1次或者部分2次张拉，并且在中间施工阶段过程中各个部分内力、应力和位移满足要求，最后得到的成桥吊杆索力和设计值接近。故可选设计吊杆索力和优化后的吊杆索力差值列阵二范数平方的最小值作为目标函数，即

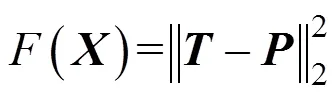
式中：为成桥阶段吊杆设计索力列阵。

由于在张拉过程中，拱桥的刚度较大，位移变化较小，同时各个材料本构特性近似满足线性关系，因此整个结构体系满足线性叠加原理。引入影响矩阵法，由式(7)可以得到：

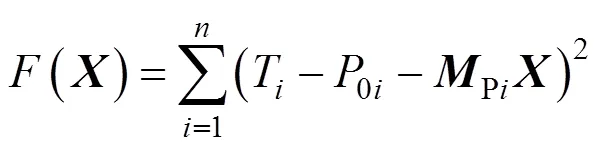
式中：T为成桥阶段第个吊杆的设计索力值；0i为吊杆张拉前时第个吊杆的初始索力值；Pi为吊杆索力影响矩阵的第行。

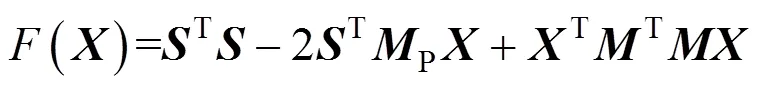
将式(9)改写为：

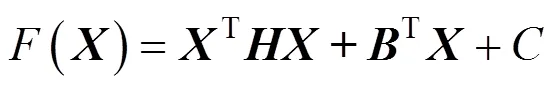
1.3 吊杆张拉索力的优化模型

选取约束条件为各个吊杆张拉的施工阶段内的主梁、拱肋的挠度、应力以及吊杆索力都小于规定的限值。综合考虑，得到吊杆张拉优化模型如下：

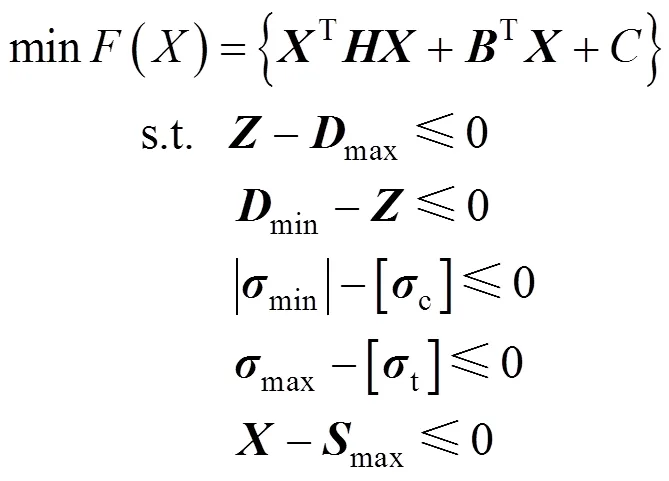
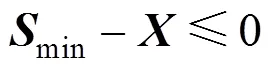
以上数学模型为有约束的二次规划问题，求解这类问题主要有搜索法和求解KT方程法两大类。其中求解KT方程法是先用Lagrange乘子法将其转化为无约束问题，再利用Kuhn-Tucker条件或把KT方程化为线性互补问题，采用互补主元法求解[12]。而对于凸规划而言，KT方程是条件极值问题的充要条件，其局部极小值就是整体的最小值。上述数学模型中二次项系数H为正定矩阵，故此二次规划为严格凸二次规划，只需找到KT点即可求解。根据以上分析，本文采用MATLAB软件中的quadprog函数进行求解，得到优化后各施工阶段吊杆张拉力。整个求解流程如图1所示。

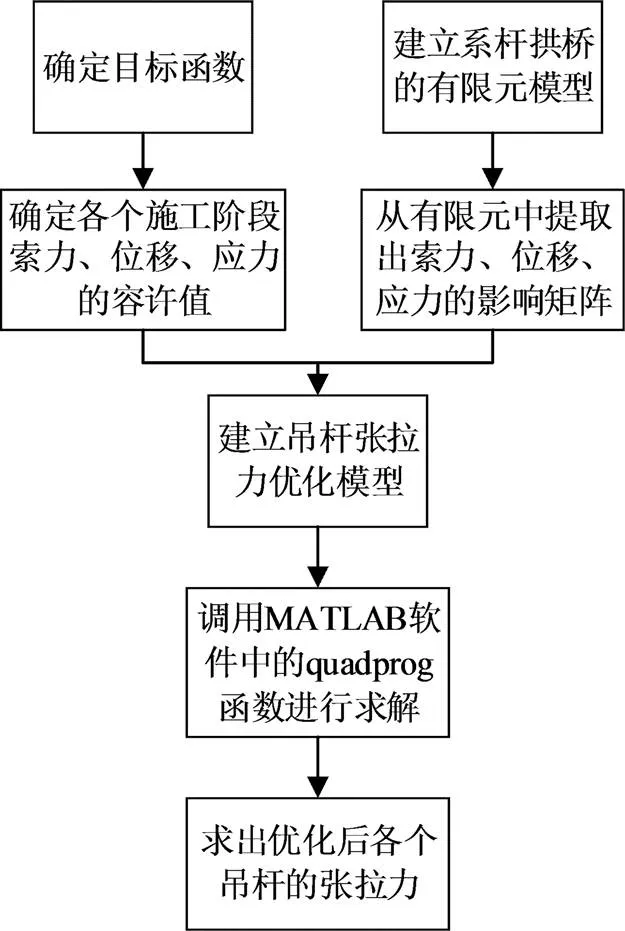
图1 优化计算流程图

2 工程实例

2.1 背景工程

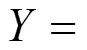
2.2 有限元模型

全桥采用有限元分析软件MIDAS Civil进行结构的离散和有限元模型的建立，系梁截面按照实际的单箱三室箱形截面模拟，在横隔板处采用线性变截面。拱肋按照实际的哑铃型截面来模拟，采用施工联合截面来模拟拱肋钢管、管内混凝土和拱肋腹板混凝土在不同的施工阶段施工，拱脚采用矩形截面模拟。模型中采用的主要参数见表1。

单位：cm

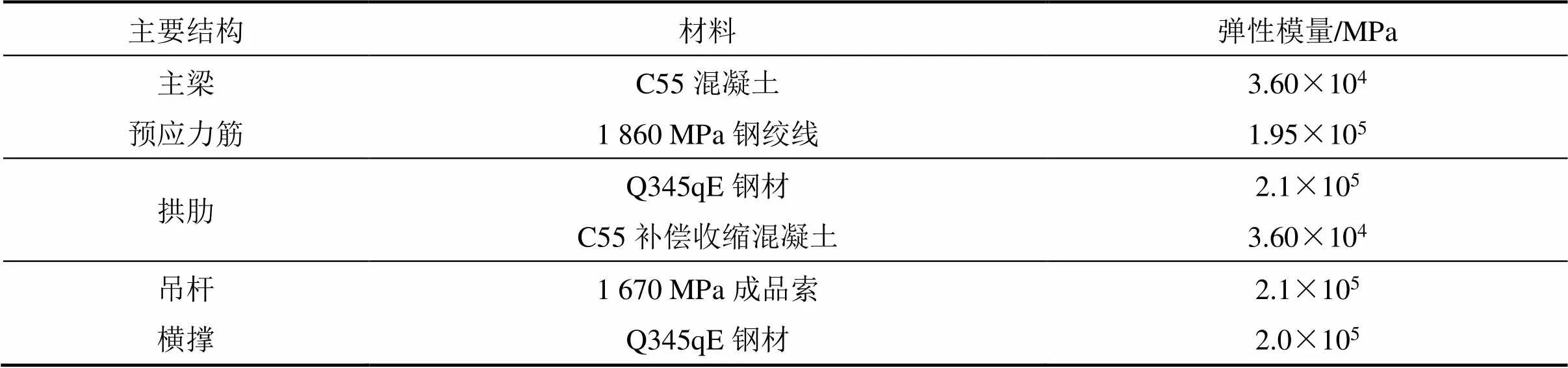
表1 全桥主要建模参数

全桥总共划分543个节点和548个单元，其中梁单元484个，桁架单元64个，全桥有限元模型如图3所示。为了获得该桥的影响矩阵，按照实际的施工顺序划分施工阶段，对简支拱进行正装分析，充分考虑各个施工阶段荷载(自重、预应力、吊杆张拉力、温度效应、收缩徐变、二期恒载等)。

2.3 优化结果

利用建立的有限元模型，得到吊杆张拉力对吊杆索力、系梁挠度和应力、拱肋挠度和应力的影响矩阵，以优化前后吊杆成桥索力差值列阵二范数平方的最小值为目标函数，按照图1中的流程进行优化计算，得到优化后的吊杆1次张拉的张拉力。再将优化后的吊杆张拉力施加到系杆拱桥的有限元模型中进行正装分析，得到优化前后吊杆张拉力和吊杆成桥索力见表2，主梁控制截面挠度和弯矩、拱肋控制截面挠度和轴力如图4~7所示。

图3 全桥有限元模型

表2 优化前后吊杆张拉力及吊杆成桥索力

注：表中成桥阶段是指张拉完所有吊杆，还未进行拆除支架和施加二期恒载等工序的阶段。

表2为优化前后吊杆张拉力及吊杆成桥索力，可以看出，优化后吊杆1次张拉力和设计2次张拉的第2次张拉力大致相等，优化后的吊杆索力与设计索力十分接近，最大偏差为−4.6%，小于±5%，达到1次张拉和设计2次张拉的吊杆索力相接近的优化目标。

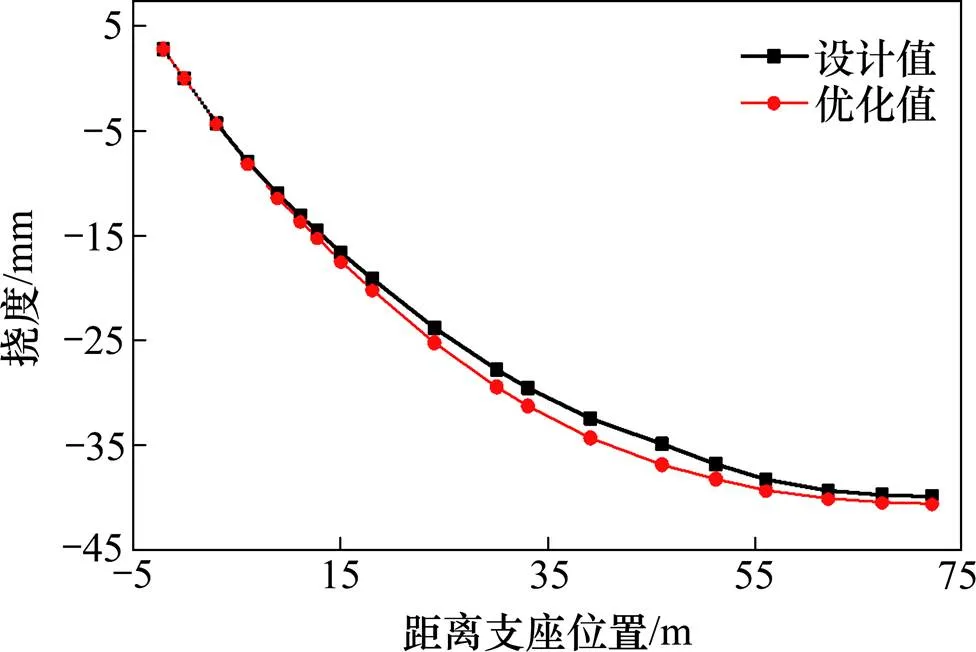
图4 系梁恒载挠度

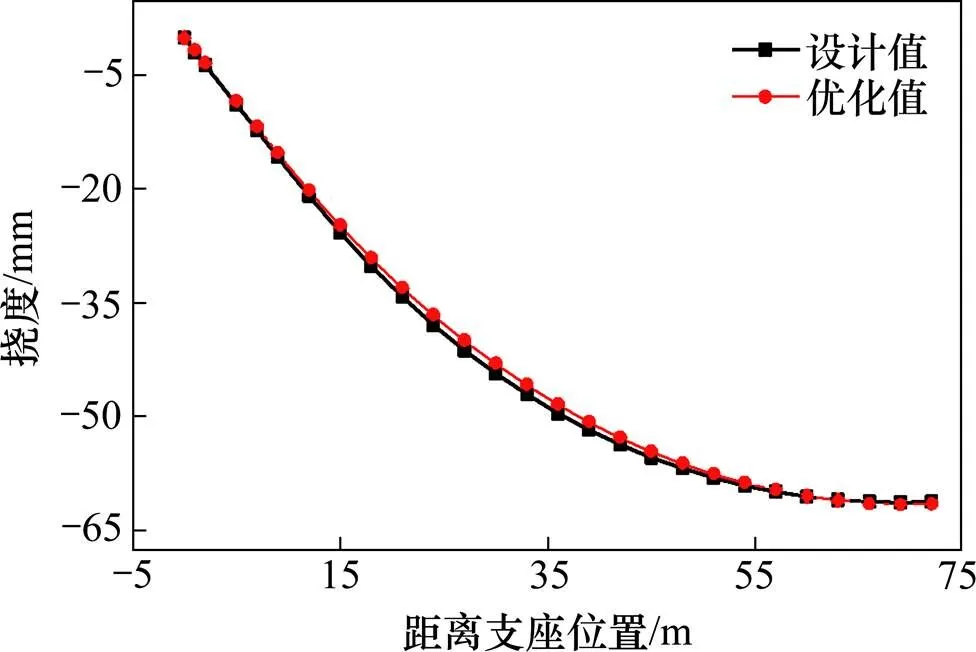
图5 拱肋恒载挠度

图4和图5为在恒载作用下，成桥阶段的系梁和拱肋各个控制截面按设计索力张拉和按优化后张拉的挠度对比。可以看出，优化后吊杆1次张拉和设计2次张拉系梁的挠度在支座附近截面和跨中附近截面基本相等，大约在1/4位置附近两者挠度差值达到最大。优化后拱肋的挠度在各个控制截面基本都相等，最大挠度差值在大约拱肋1/4处，最大差值百分数为4.7%。

图6为恒载作用下系梁弯矩图，由图6可以得到，在恒载作用下，成桥阶段系梁弯矩在优化前后基本相等，优化后的弯矩较设计值在支座附近处略微增大，在跨中处则有所减小。图7为恒载作用下拱肋轴力图，由图7可以看出，在恒载作用下，成桥阶段拱肋截面的轴力整体满足从跨中到拱脚截面处逐渐增大的规律，和实际相符。拱桥轴力在拱脚截面处优化前后差值最大，最大差值的百分数仅为0.64%。

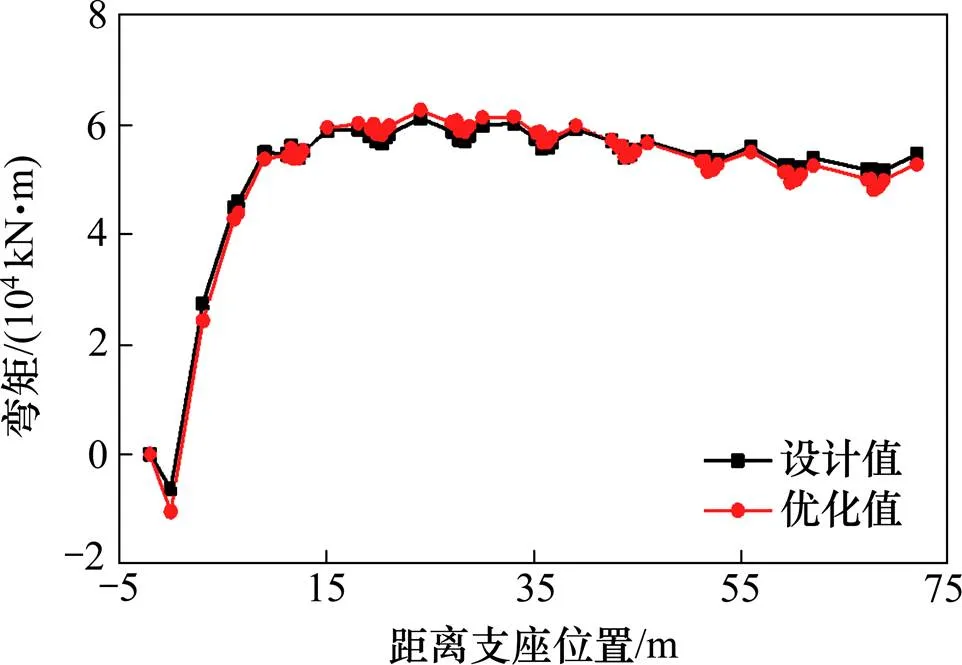
图6 系梁恒载弯矩

图7 拱肋恒载轴力

3 结论

1) 引入影响矩阵法，建立考虑施工阶段系杆拱桥的吊杆张拉优化模型。通过优化模型，得到优化后的吊杆张拉力，使得优化后吊杆的成桥索力和设计成桥索力相接近，达到在不改变成桥索力的基础上，减少吊杆张拉次数、节省施工成本、简化施工过程和缩短施工工期的目的。

2) 利用本文提出的方法，对新建某高速铁路144 m下承式无砟双线尼尔森体系简支拱的吊杆张拉进行优化，将施工过程中吊杆的张拉次数由2次减为1次，减少施工成本和缩短工期，同时降低了多次调索的反复性和不确定性。

3) 在满足施工和成桥的要求下，优化后吊杆1次张拉成桥，系梁和拱肋的挠度、内力与设计状态较接近，验证了该优化模型的可靠性和有效性。该优化方法可为同类型桥梁的设计和施工提供参考。

[1] 霍明刚. 大跨径下承式钢管混凝土系杆拱桥吊杆张拉力控制优化分析[D]. 兰州: 兰州交通大学, 2014: 1−6. HUO Minggang. The tension control optimization analysis of tied arch bridge suspender of long-span steel pipe concrete under the deck[D]. Lanzhou: Lanzhou Jiaotong University, 2014: 1−6.

[2] 张谢东, 曹鹏, 许精文. 尼尔森体系系杆拱桥结构分析[J]. 桥梁建设, 2009(6): 23−26. ZHANG Xiedong, CAO Peng, XU Jingwen. Structural analysis of tied arch bridge of Nielsen system[J]. Bridge Construction, 2009(6): 23−26.

[3] Hassan M M, Nassef A O, Damatty A A E. Determination of optimum post-tensioning cable forces of cable-stayed bridges[J]. Engineering Structures, 2012, 44(44): 248− 259.

[4] 张石波, 裴若娟. 浅谈尼尔森体系的钢管混凝土提篮拱在铁路桥梁中的运用前景[J]. 桥梁建设, 2001(4): 56−58. ZHANG Shibo, PEI Ruojuan. Brief account on the application of Nielsen system concrete-filled steel tube A-shaped arch in railway bridges[J]. Bridge Construction, 2001(4): 56−58.

[5] 李佳序. 温度作用对在役尼尔森体系钢管混凝土拱桥影响的研究[D]. 石家庄: 石家庄铁道大学, 2017: 3−4. LI Jiaxu. Study on the effect of temperature on concrete-filled steel tubular arch bridge of Nielsen system[D]. Shijiazhuang: Shijiazhuang Tiedao University, 2017: 3−4.

[6] 楚海建, 何结兵, 顾爱军, 等. 系杆拱桥吊杆一次张拉方案的优化设计[J]. 华东公路, 2002(1): 46−48. CHU Haijian, HE Jiebing, GU Aijun, et al. Optimization design of one tensioning scheme for tie rod arch bridge[J]. East China Highway, 2002(1): 46−48.

[7] 张文丰, 胡成. 影响矩阵法在斜拉桥施工调索中的应用[J]. 工程与建设, 2018, 32(6): 91−95. ZHANG Wenfeng, HU Cheng. Application of influence matrix method in construction regulation of cable-stayed bridge[J]. Engineering and Construction, 2018, 32(6): 91−95.

[8] 肖汝诚, 项海帆. 斜拉桥索力优化及其工程应用[J]. 计算力学学报, 1998, 15(1): 118−126. XIAO Rucheng, XIANG Haifan. Optimization method of cable prestresses of cable-stayed bridges and its engineering applications[J]. Chinese Journal of Computational Mechanics, 1998, 15(1): 118−126.

[9] 陶海, 沈祥福. 斜拉桥索力优化的强次可行序列二次规划法[J]. 力学学报, 2006, 38(3): 381−384. TAO Hai, SHEN Xiangfu. Strongly subfeasible sequential quadratic programming method of cable tension optimization for cable-stayed bridges[J]. China Journal of Theoretical and Applied Mechanics, 2006, 38(3): 381−384.

[10] 肖汝诚, 项海帆. 斜拉桥索力优化的影响矩阵法[J]. 同济大学学报(自然科学版), 1998, 26(3): 235−240. XIAO Rucheng, XIANG Haifan. Influence matrix method of cable tension optimization for cable-stayed bridges[J]. Journal of Tongji University (Natural Science), 1998, 26(3): 235−240.

[11] 梁鹏, 肖汝诚, 张雪松. 斜拉桥索力优化实用方法[J].同济大学学报(自然科学版), 2003, 31(11): 1270−1274. LIANG Peng, XIAO Rucheng, ZHANG Xuesong. Practical method of optimization of cable tensions for cable-stayed bridges[J]. Journal of Tongji University (Natural Science), 2003, 31(11): 1270−1274.

[12] 田志昌, 孙超, 韩永华, 等. 拱桥成桥状态下吊杆索力优化[J]. 铁道科学与工程学报, 2017, 14(2): 296−302. TIAN Zhichang, SUN Chao, HAN Yonghua, et al. Completed bridge suspender forces optimization of a arch bridge[J]. Journal of Railway Science and Engineering, 2017, 14(2): 296−302.

[13] 王学明, 李平. 矮塔斜拉桥拉索初张力优化[J]. 铁道工程学报, 2005(4): 39−42. WANG Xueming, LI Ping. Cable initial tension optimized design of extradossed bridge[J]. Journal of Railway Science and Engineering, 2005(4): 39−42.

[14] GAO Qiong, YANG Menggang, QIAO Jiandong. A multi-parameter optimization technique for prestressed concrete cable-stayed bridges considering prestress in girder[J]. Sructural Engineering and Mechanics, 2017, 64(5): 567−577.

[15] 李小年. 自锚式悬索桥合理成桥状态确定及吊索张拉优化研究[D]. 长沙: 中南大学, 2009: 12−15. LI Xiaonian. Rational completion status and optimization of hanger tension of self-anchored suspension bridge[D]. Changsha: Central South University, 2009: 12−15.

[16] 杨俊. 基于影响矩阵的大跨桥梁合理成桥状态与施工控制研究[D]. 武汉: 武汉理工大学, 2008: 16−18. YANG Jun. Determination of rational completion status of cable-stayed bridges[D]. Wuhan: Wuhan University of Technology, 2005: 16−18.

Study on optimization of suspender tension of a high-speed railway tied-arch bridge considering construction stage

WANG Xiangguo1, DENG Bo2, YANG Menggang2

(1. China State Railway Investment Construction Group Co., Ltd, Beijing 110020, China; 2. School of Civil Engineering, Central South University, Changsha 410075, China)

Aimed to decrease the time of suspender tension by performing optimization research considering construction, the influence matrix method is drawn into to establish the optimization model in which the two-norm square minimum value of the cable force difference before and after optimization is considered as the objective function, the tensile force as a variable, the cable force as well as the deflection and stress of the beam and arch rib as the constraint condition. Based on the optimization model, taking a high-speed railway simply supported tied-arch bridge with the span of 144 meters for high-speed railway as an example, the tensile forces of the suspenders are obtained with the proposed optimization model ensuring that each suspender only needs to be stretched once. The result shows that the deflections and internal forces of the beam and arch rib stretched once are close to the design state, which verifies the reliability and validity of the optimization model and can provide a reference for design and construction of bridges with similar structures.

tied-arch bridge; suspender tension; optimization model; construction stage; influence matrix

U24

A

1672 − 7029(2020)04 − 0808 − 07

10.19713/j.cnki.43−1423/u.T20190604

2019−07−05

国家自然科学基金面上资助项目(51978667)

杨孟刚(1976−)，男，江西安义人，教授，博士，从事桥梁抗震与设计理论研究；E−mail：mgyang@csu.edu.cn

(编辑 阳丽霞)