基于三维轮轨瞬态动力学模型的钢轨波磨不平顺动力影响与识别

周成，高建敏

基于三维轮轨瞬态动力学模型的钢轨波磨不平顺动力影响与识别

周成，高建敏

(西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

应用有限元理论及ANSYS/LS-DYNA有限元仿真软件，建立三维轮轨瞬态动力学模型，分析高速铁路钢轨波磨不平顺对轮轨系统动力响应的影响特征，在此基础上，探讨钢轨波磨不平顺的识别方法。研究结果表明：钢轨波浪形磨耗会导致轮轨系统产生剧烈的高频振动，在钢轨实测波磨不平顺激扰作用下，轮轨垂向力、轴箱和钢轨垂向振动加速度等轮轨垂向动力学指标均表现出明显的高频振动特征，其高频振动频率范围位于500~700 Hz，与相同速度条件下，实测钢轨波磨不平顺的主要波长成分对应；通过对轮轨系统动力响应指标进行小波包时频分析，可有效识别出钢轨波磨不平顺的波长与纵向位置。相关研究成果可为高速铁路钢轨表面短波不平顺的研究及钢轨波磨不平顺的养护维修管理提供参考。

高速铁路；轮轨瞬态动力学模型；钢轨波磨不平顺；高频振动；识别

中国高速铁路的迅速发展，极大地方便了人们的出行，促进了经济的发展，但同时也有许多疑难棘手的问题伴随而来，钢轨波浪形磨耗(波磨)就是其中非常突出的问题。钢轨波浪形磨耗是指钢轨的纵向面产生了具有一定规律性、周期性、波浪形的磨耗现象，它严重影响到列车运行的平稳性和安全性。列车在波浪形磨耗钢轨上运行时，轮对与钢轨之间将产生频繁变化的轮轨力，更有甚者，当车辆运行在短波长波浪形磨耗钢轨或波纹磨耗钢轨上时，轮轨间由于更为频繁的作用力，会导致轮对出现瞬时脱离钢轨的情况，导致轮轨间产生更大的轮轨高频冲击力[1]，列车运行的安全性将受到巨大的威胁，乘客的乘坐品质也将会显著降低。并且，在对钢轨波磨不平顺进行检测时，通常采用的是直接测量的方法，极大地增加了工作人员的工作量。因此，研究高速行车条件下，钢轨波磨对轮轨系统的动力影响特征，进而探讨钢轨波磨不平顺的识别方法，这对高速铁路的安全、平稳运营以及钢轨波浪形磨耗不平顺的养护维修管理具有十分重要的意义。由于钢轨波磨问题之重要，国内外专家学者对此开展了深入研究。Clark[2]为了准确了解钢轨波磨对车辆－轨道系统造成的动力学影响，开发了一套数学模型，仿真计算了钢轨波磨条件下轮轨系统的动力学响应，并将结果与试验数据进行了比较。Neilsen[3]建立了轮对与波磨钢轨非线性滚动接触模型，通过分析指出，当轮轨法向力、纵向牵引力以及轮轨蠕滑不发生改变时，由于轮轨间的非线性接触，钢轨的磨耗会发生恶化，并且通过研究，预测了钢轨波磨不平顺波长的增长率，给出了钢轨波磨不平顺波长的临界值。WANG等[4]建立了车辆－轨道耦合动力学空间模型，计算了实测钢轨波磨不平顺激扰下的轮轨力、车辆和钢轨振动加速度等响应，分析了波磨不平顺对轮轨动力响应的影响规律。赵鑫等[5]建立了半轮对－钢轨的三维瞬态滚动接触有限元模型，利用隐式积分与显式积分相结合的求解方法，对我国某波磨轨道进行了仿真分析。结果表明，当车辆通过波磨钢轨时，所产生的轮轨力与钢轨波磨的相位并不同相，相位差与车辆运行速度有关。司道林等[6]利用多体动力学软件NUCARS建立了车辆动力学模型，研究分析了钢轨磨耗指数与车辆簧下质量、一系悬挂以及扣件刚度和阻尼的关系，提出了一些降低钢轨波浪形磨耗的措施。朱崇巧[7]基于车辆－轨道耦合动力学理论，计算了大量钢轨波磨不平顺工况下的轮对垂向加速度响应，并且分别利用Hilbert-Huang变换、小波包变换、以及双谱方法对轮对垂向加速度进行分析。综合上述研究可见，各国专家学者在钢轨波磨不平顺对轮轨系统的动力影响、钢轨波磨不平顺的识别等方面都开展了相关研究。然而，在建立车辆(车轮)与磨耗钢轨动力分析模型时，并未充分考虑轮对、钢轨的弹性变形或者尽管模型中考虑了轮、轨的弹性变形，但对钢轨波磨不平顺动力影响的分析又不充分，钢轨波磨不平顺识别研究方面也有待补充。因而，本文将上述2方面研究相结合，考虑到钢轨波磨不平顺将导致轮轨产生高频振动响应之特点，利用有限元软件ANSYS/LS-DYNA建立三维轮轨瞬态动力学模型，考虑轮对、钢轨弹性变形，利用隐式−显式顺序求解方法，研究钢轨波磨不平顺对轮轨系统高频振动的动力影响特征，在此基础上，探讨钢轨波磨不平顺的识别方法。

1 三维轮轨瞬态动力学有限元模型

三维轮轨瞬态动力学有限元模型可将轮对、钢轨等结构部件考虑成柔性体，通过对车轮与钢轨进行精细化建模，可实现钢轨波磨不平顺激扰作用下轮轨系统高频振动动力响应的仿真计算分析。

1.1 模型的建立

根据某类型高速车辆与某条高速铁路线路的实际参数建立了三维轮轨瞬态动力学有限元模型。考虑到本文的研究重点是车辆通过钢轨波浪形磨耗段时的动力学行为，重点关注的是轴箱垂向加速度(以轮轴端端部某节点垂向加速度代替，下同)、钢轨垂向加速度(以钢轨轨底某节点垂向加速度代替，下同)、轮轨垂向力等高频振动信息的分析，而波磨不平顺激扰作用下车辆－轨道系统的高频振动主要是由轮对和钢轨的柔性来决定，因此，对车辆－板式轨道系统结构进行了简化，其结构简图如图1所示。

建模中，主要考虑车辆的簧上质量，一系悬挂的刚度和阻尼，轮对、钢轨、扣件的刚度和阻尼，轨道板等一些结构部件及其属性。其中，由于簧上质量是直接通过一系悬挂施加在轮对上的，因此，将簧上质量平均分成多个质量点通过一系悬挂加载到轮轴的两端。由于所选轨道为直线段轨道，忽略轮对的横移，因此，一系悬挂并不需要提供横向刚度，可将一系悬挂简化成多根弹簧、阻尼元件，只提供垂向刚度和垂向阻尼。轮对、钢轨建模时，充分考虑轮对、钢轨的真实尺寸。轮对踏面采用LMA型踏面，公称直径为915 mm，采用实体单元建模；钢轨采用60 kg/m轨，钢轨长度为14.04 m，也是采用实体单元建模。因为扣件既需要提供垂向的刚度和阻尼也需要提供横向的刚度和阻尼，因此，作者在ANSYS隐式分析中使用三向弹簧来模拟扣件，而在LS-DYNA显式分析中采用beam单元来模拟扣件，扣件的横向刚度和横向阻尼通过在钢轨轨底侧面添加横向beam单元进行模拟。考虑本文建模的结构特点，为保证扣件能更加均匀的支承钢轨，故在一个扣件位置处建立多个弹簧单元。轨道板根据其真实尺寸进行实体建模。模型的详细参数[1]如表1所示。

图1 轮轨系统结构简图

在建模划分网格过程中需要特别注意的是，为保证模型仿真计算结果的准确性，同时又不耗费大量的计算时间，将轮对踏面与钢轨接触的区域进行细化网格划分，将钢轨波磨区域也同样进行细化网格划分，其它区域的网格划分则可以略大些。模型网格划分如图2和图3所示。经过不等分网格划分后，所建模型共有102.7万个节点，108.4万个单元。由于轮对与钢轨间是滚动接触，因此，在设置轮轨间的接触状态时，采用罚函数“面−面”接触法来模拟。设置模型边界条件为：轨道板底部全约束，钢轨两端约束横向位移与纵向位移，簧上质量点约束横向位移。

表1 模型参数

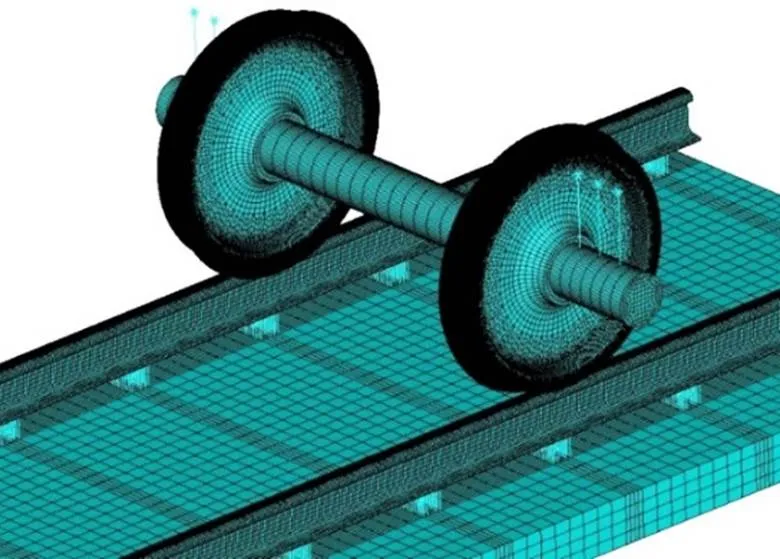
图2 模型网格划分

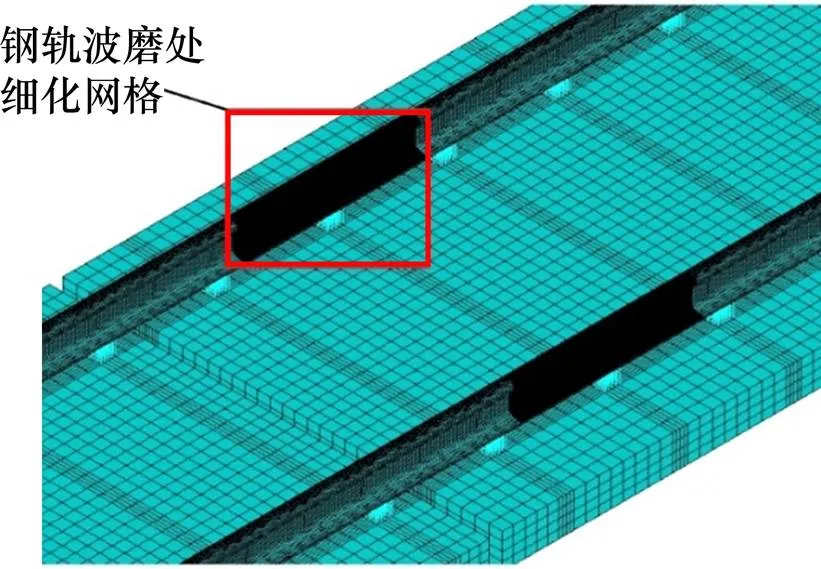
图3 钢轨波磨段网格划分

1.2 求解方法

有限元积分方法主要包括隐式积分和显式积分。隐式积分是根据当前时刻及其前几时刻的动力响应值建立下一时刻动力响应值为未知量的线性方程组,通过求解方程组确定下一时刻动力响应值，耗时较长，但是，隐式积分的过程是无条件稳定的；显式积分可由当前时刻及其前几时刻动力响应值直接计算下一时刻动力响应值，将在很大程度上节约计算时间，节省计算机的计算资源，但是，显式积分需要控制好求解的时间步长，以免系统的计算出现不稳定现象。由于本文所建的模型规模较大，且分析的是瞬态动力学问题，综合考虑隐式积分与显式积分的优缺点，最终选择采用隐式—显式顺序求解的方法[10]来对所建立的模型进行数值分析求解计算，其求解过程如下。

首先利用隐式积分方法计算轮对在初始位置时，在轮轨模型自重条件下，整个模型的变形状态；以隐式计算结果为模型的初始状态，再添加其它初始条件，并施加载荷，利用显式积分方法求解轮对在轨道上滚动的瞬态动力学行为，数值分析计算大致过程如图4所示。

图4 数值分析过程

1.3 模型验证

轮轨动态作用力是衡量机车车辆对轨道动态作用的最重要指标[1]。为此，本文以轮轨垂向力指标为例，分析所建模型的正确性。为保证仿真计算的初始条件与文献[5]尽可能一致，设置车辆运行速度为300 km/h，仿真时间为0.12 s，轨道不平顺选择一段长度为1 m，波长为0.08 m，波深为0.14 mm的余弦型钢轨波磨不平顺数据，如图5所示。图5所示的波磨不平顺数据与文献[5]中所采用的钢轨波磨不平顺相同。利用所建模型计算了钢轨波磨不平顺激扰作用下轮轨系统的动力响应情况，并与文献[5]中的轮轨垂向力进行了比较，对比结果如图6所示。

图5 余弦型钢轨波磨不平顺

图6 轮轨垂向力响应计算结果对比

由图6可以看出，本文模型计算出的轮轨垂向力波形与文献[5]中的轮轨垂向力波形基本一致；本文计算的最大轮轨垂向力值为155 kN，文献[5]中轮轨垂向力最大值为190 kN，相差较大，这主要是因为两者采用的车辆轴重不同，文献[5]中的静轮重约为88 kN，而本文模型中的静轮重仅为75 kN。而反映轨道不平顺对轮轨垂向力的动力影响还可以通过轮轨垂向力的动静比来表示。通过计算两者轮轨垂向力的最大动静比发现，本文模型计算的轮轨垂向力最大动静比为2.07，而文献[5]中轮轨垂向力最大动静比为2.16，两者相差不大。

此外，还计算分析了不同轨道不平顺激扰作用下轴箱振动加速度和钢轨振动加速度等指标，并与相关文献资料[1, 8−9]进行对比。对比结果显示本文所建的三维轮轨瞬态动力学模型是可靠的，计算结果较为准确。

2 钢轨波磨不平顺对轮轨系统的动力影响特征

采用本文所建模型，计算了高速铁路现场实测波磨不平顺激扰作用下，轮轨系统的动力学响应特征。仿真计算时，车辆运行速度为300 km/h，钢轨波磨不平顺为某高速铁路上实测数据，长度为10 m，如图7所示。

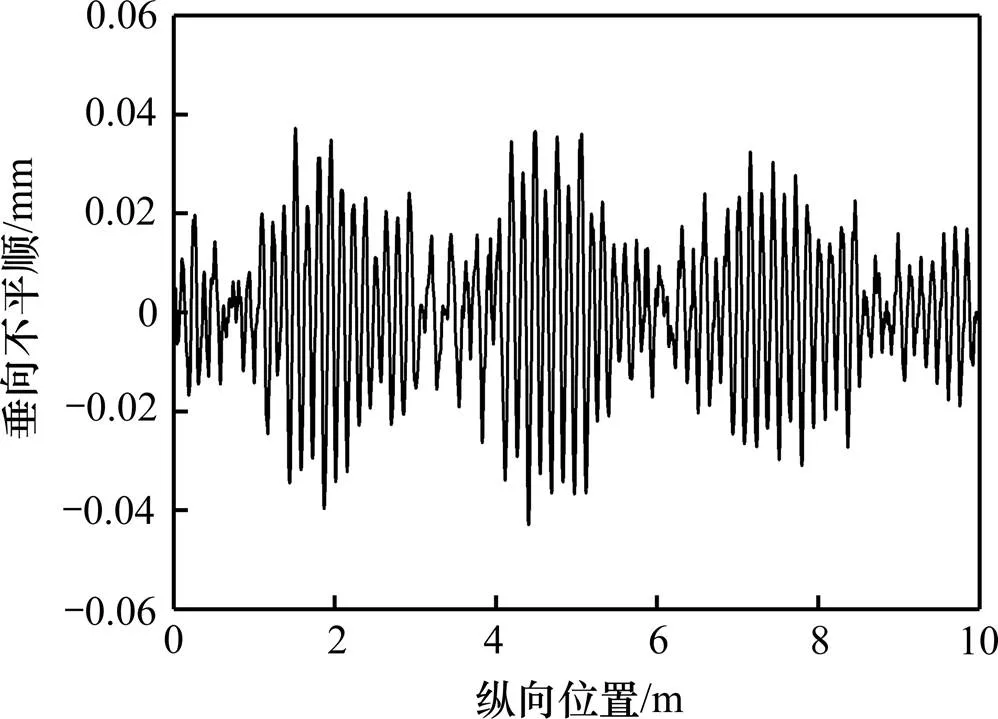
图7 实测钢轨波磨不平顺

图8~10分别给出了实测钢轨波磨不平顺激扰条件下，轮轨垂向力、轴箱垂向振动加速度和钢轨垂向振动加速度响应曲线及其频谱图。

由图8~10可以看出，轮对在运行到钢轨波磨区域时受到了剧烈的高频冲击，轮轨垂向力、轴箱和钢轨垂向振动加速度指标均出现明显的高频振动特征，轮轨垂向力的最大值达到了120 kN，而轴箱和钢轨的垂向振动加速度指标最大值则分别达到了25.73和117.6。进一步对轮轨垂向力、轴箱和钢轨垂向振动加速度做频谱分析发现，轮轨垂向力高频率成分主要集中在562~600 Hz，轴箱和钢轨垂向振动加速度的高频率成分分别集中在558~624 Hz和531~670 Hz，各指标均存在明显的高频振动响应，且三者对应的高频振动频率范围较为一致，集中在500~700 Hz范围之内。利用公式，可求得三者的频率对应的波长范围分别是0.139~ 0.148 m，0.134~0.149和0.124~0.157 m。而通过对钢轨波磨不平顺数据进行频谱分析，分析其主要波长成分发现，该实测波磨不平顺的波长主要集中在0.132~0.152 m，与上述通过3项轮轨动力响应指标计算出的波长范围都较为接近，如图11所示。这也再此印证了，钢轨波磨不平顺会激发轮轨间的高频振动，是高速铁路轮轨高频振动的主要影响因素，同时也说明，采用三维轮轨瞬态动力学有限元模型可以分析高速铁路钢轨波磨不平顺对轮轨系统的动力影响，且动力学响应结果能有效地反映出钢轨波磨不平顺的主要波长成分。

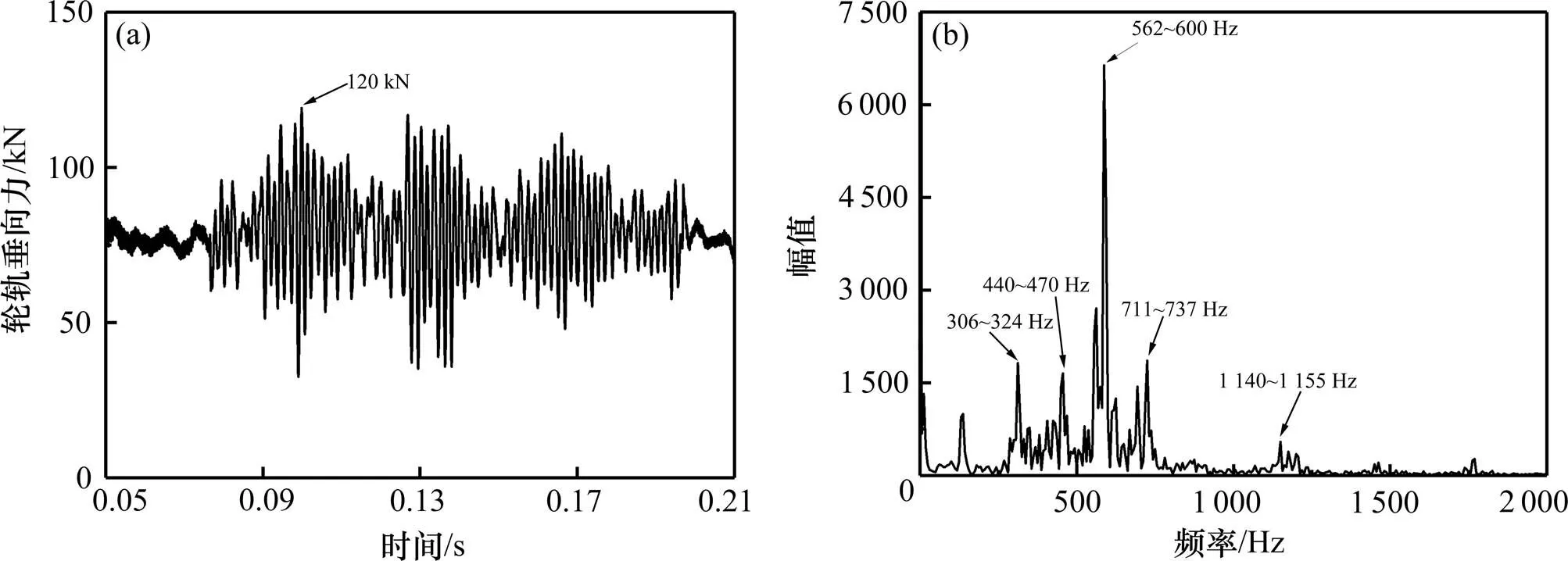
(a) 时程曲线；(b) 频谱图

(a) 时程曲线；(b) 频谱图

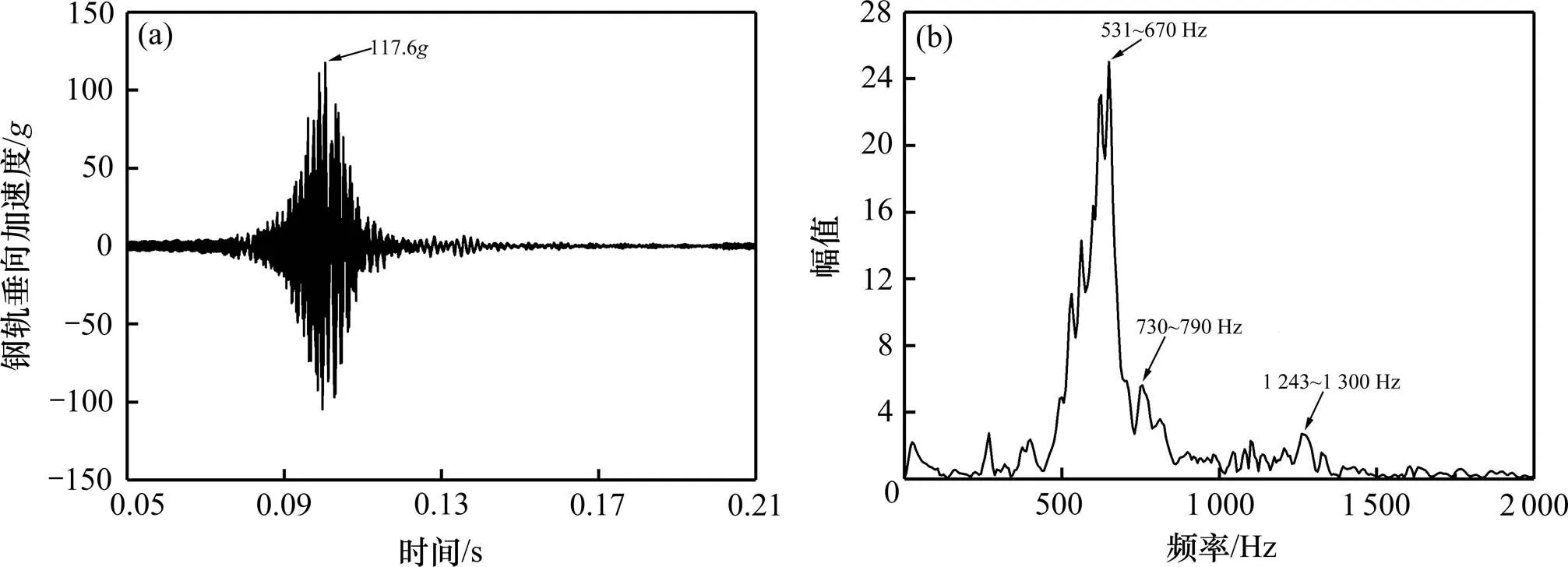
(a) 时程曲线；(b) 频谱图

图11 实测波磨不平顺波长成分分析

综上分析发现，钢轨波磨不平顺对轮轨系统的高频冲击振动影响明显，且通过轮轨系统的动力响应特征可以判断出钢轨波磨不平顺的主要波长成分。为此，通过对轮轨系统动力响应指标进行分析，探讨钢轨波磨不平顺的识别方法。

3 钢轨波磨不平顺识别研究

对于钢轨波磨不平顺的识别，通常采用的是直接测量的方法，不仅会占用轨道，而且会极大的增加工作人员的工作量。因此，找到一种易测量且有效的指标，间接识别钢轨波磨不平顺是确切需要的。为此，本节基于上述钢轨波磨不平顺激扰下的轮轨系统动力响应指标和小波包分析理论，来探讨钢轨波磨不平顺的识别方法。

3.1 小波包分析理论

多分辨率分析是在1988年被提出的概念，通过对信号进行降采样处理，得到细化的信号特征。但是，多分辨率分析只对信号的低频部分不断进行分解，而忽略了其高频部分，针对这一缺陷，Wickerhauser等提出了小波包分析。与多分辨率分析相比，它将未分解的高频成分也做与分解低频相同的方法进行逐步分解，提高了对信号的分析能力[11]。如图12所示，为3层小波包分解的结构树[11]。

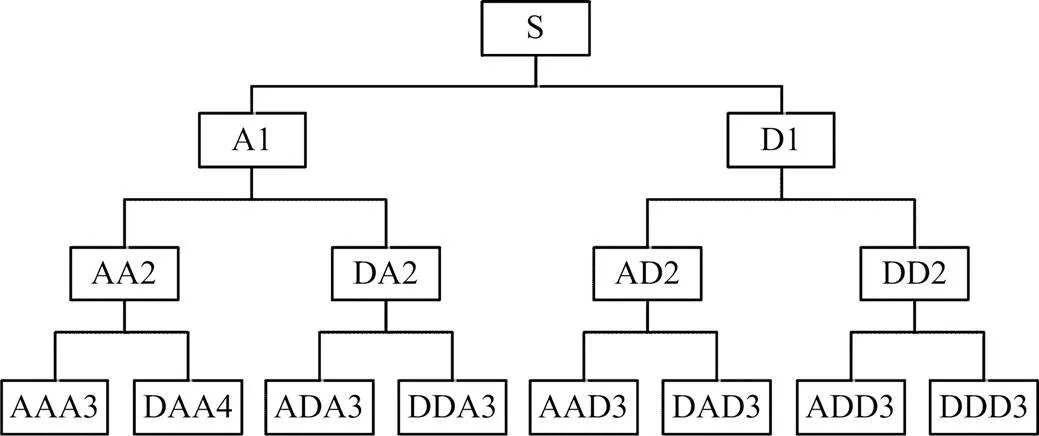
图12 小波包分解树

3.2 钢轨波磨不平顺的识别分析

基于第2节的研究发现，钢轨波磨不平顺对轮轨系统动力响应产生了明显的影响，轮轨垂向力与轴箱垂向振动加速度是反映轮轨系统高频振动的两个重要指标，由图7和图11可知，该实测钢轨波磨不平顺主要波长约为0.14 m，主要波深约为0.04 mm和0.08 mm。因此，设置车辆运行速度为300 km/h，以波长为0.14 m，波深分别为0.04 mm和0.08 mm的钢轨波磨不平顺激扰下的轮轨垂向力和轴箱垂向振动加速度指标为例，通过对其进行小波包时频分析来开展钢轨波磨不平顺识别研究。

图13和图14给出了轮轨垂向力与轴箱垂向加速度的小波包时频分析图，图中下侧横坐标表示车辆运行时间，左侧纵坐标表示振动频率，右侧纵坐标可认为是与能量正相关的量。由图13和图14可以看出，在钢轨波磨不平顺激扰下，轮轨垂向力与轴箱垂向加速度小波包时频图特征明显。4幅图中的亮斑区域中心对应的频率均约为600 Hz，利用公式，可求得对应的波长为0.139 m，这与波磨的波长0.14 m相接近；对应的车辆运行时间均约为0.076~0.090 s，利用公式，可求得对应的车辆运行的纵向位置为6.33~7.5 m，这与模型中的波磨区域6.38~7.38 m相接近。

(a)轮轨垂向力；(b)轴箱垂向加速度

(a)轮轨垂向力；(b)轴箱垂向加速度

分别对比图13与图14中的轮轨垂向力与轴箱垂向加速度的时频图发现，在波长相同波深不同的波磨不平顺激扰下，波深越大，亮斑区域对应的能量越大，因此，此方法只能对钢轨波磨不平顺的波深进行相对识别。综上可知，通过对轮轨系统动力响应指标进行小波包时频分析，可有效识别出钢轨波磨不平顺的波长与纵向位置，但只能对波磨不平顺的波深进行相对识别。

4 结论

1) 所建立的三维轮轨瞬态动力学有限元模型能有效的反映钢轨波磨不平顺动力影响的主要波长成分，可用于不同行车条件下钢轨波磨不平顺的动力影响分析。

2) 钢轨波磨不平顺激扰作用下，高速铁路轮轨系统受到了剧烈的高频冲击振动影响，轮轨垂向力、轴箱和钢轨垂向振动加速度等轮轨垂向动力学指标均出现明显的高频振动特征，且三者的高频振动频率范围较为一致，集中在500~700 Hz之间。

3) 通过对轮轨系统动力响应指标进行小波包时频分析，可有效识别出钢轨波磨不平顺的波长与纵向位置，但只能对波磨不平顺的波深进行相对识别。

[1] 翟婉明. 车辆－轨道耦合动力学[M]. 4版. 北京: 科学出版社, 2015.ZHAI Wanming. Vhicle-track coupled dynamics[M]. 4th ed. Beijing: Science Press, 2014.

[2] Clark. An investigation into the dynamic effects of railway vehicles running on corrugated rails[J]. Mech Eng Sci, 1982, 24(2): 65–76.

[3] Neilsen J B. Evolution of rail corrugation predicted with a non-linear wear model[J]. Elsevier, 1999, 227: 915− 933.

[4] WANG Kaiyun, LIU Pengfei, ZHAI Wanming, et al. Wheel/rail dynamic interaction due to excitation of rail corrugation in high-speed railway[J]. Science China Technological Sciences, 2015, 58(2): 226−235.

[5] 赵鑫, 温泽峰, 王衡禹, 等. 三维高速轮轨瞬态滚动接触有限元模型及其应用[J]. 机械工程学报, 2013, 49(18): 1−7. ZHAO Xin, WEN Zefeng, WANG Hengyu, et al. 3D transient finite element model for high-speed wheel-rail rolling contact and its application[J]. Journal of Mechanical Engineering, 2013, 49(18): 1−7.

[6] 司道林, 李伟, 杜香刚. 减缓高速铁路钢轨波磨的仿真分析[J]. 中国铁道科学, 2014, 35(6): 79−83. SI Daolin, LI Wei, DU Xianggang. Simulation analysis on mitigating rail corrugation for high speed railway[J]. China Railway Science, 2014, 35(6): 79−83.

[7] 朱崇巧. 钢轨波浪形磨耗检测算法研究[D]. 北京: 北京交通大学, 2018. ZHU Chongqiao. Research on detection algorithm for rail corrugation[D]. Beijing: Beijing Jiaotong University, 2018.

[8] 高建敏, 翟婉明. 高速铁路钢轨焊缝区不平顺的动力效应及其安全限值研究[J]. 中国科学: 技术科学, 2014, 44(7): 697−706. GAO Jianmin, ZHAI Wanming. Dynamic effect and safety limits of rail weld irregularity on high-speed railway[M]. Science China Technological Sciences, 2014, 44(7): 679−706.

[9] 高建敏, 翟婉明, 王开云. 高速行车条件下轨道几何不平顺敏感波长研究[J]. 铁道学报, 2012, 24(7): 83−88. GAO Jianmin, ZHAI Wanming, WANG Kaiyun. Study on sensitive wavelengths of track irregularities in high- speed operation[J]. Journal of the China Railway Society, 2012, 24(7): 83−88.

[10] 莫维尼. 有限元ANSYS理论与应用[M]. 3版. 北京: 电子工业出版社, 2008Moaveni. Theory and application of finite element ansys[M]. 3rd ed. Beijing: Electronic Industry Press, 2008.

[11] 邸继征. 小波分析原理[M]. 北京: 科学出版社, 2010. DI Jizheng. Principle of wavelet analysis[M]. Beijing: Science Press, 2010.

Dynamic effect and identification of rail corrugation irregularity based on the three-dimensional wheel-rail transient dynamic model

ZHOU Cheng, GAO Jianmin

(State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)

By means of the finite element theory and ANSYS/LS-DYNA finite element simulation software, the three-dimensional wheel-rail transient dynamic model was established. By using this model, the influence of rail corrugation irregularities on the dynamic responses of wheel-rail system in high-speed railway was analyzed. On this basis, the method of identifying rail corrugation irregularities was discussed. The results show that rail corrugation will lead to obvious high-frequency wheel/rail vibrations. Under the excitation of a measured rail corrugation irregularity, the wheel-rail vertical dynamic indexes, such as the vertical wheel-rail force, axle box and rail vertical vibration accelerations, show the characteristics of high frequency vibration. The high frequency range is 500~700 Hz, which is coincident with the main wavelength of the measured rail corrugation irregularity at the same velocity. The Wavelet Packet Time-Frequency Analysis of dynamic response index of wheel-rail system can effectively identify the wavelength and longitudinal position of rail corrugation irregularities. The relevant research results can provide references for the analysis of the rail surface short wave irregularities and the maintenance management of the rail corrugation irregularities in high-speed railways.

high-speed railway; wheel-rail transient dynamic model; rail corrugation irregularities; high frequency vibration; identify

U212.2

A

1672 − 7029(2020)04 − 0841 − 08

10.19713/j.cnki.43−1423/u.T20190541

2019−06−17

国家自然科学基金资助项目(51678507)；牵引动力国家重点实验室自主研究项目(2019TPL_T10)

高建敏(1981−)，女，河北南和人，副研究员，博士，从事铁路大系统动力学理论与应用研究；E−mail；jmgao@swjtu.edu.cn

(编辑 涂鹏)